.jpg)
正确率60.0%在数列$${{\{}}$$ $${{a}_{n}}$$$${{\}}}$$中，若存在非零整数 $${{T}}$$，使得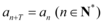
成立，则称数列$${{\{}}$$
D
A.$${{6}{7}{2}}$$
B.$${{6}{7}{3}}$$
C.$${{1}{3}{4}{4}}$$
D.$${{1}{3}{4}{5}}$$
首先，题目描述了一个数列的性质：存在非零整数 $$T$$，使得 $$a_{n+T} = a_n$$ 对所有正整数 $$n$$ 成立。这样的数列称为周期数列，$$T$$ 称为数列的周期。
题目给出了四个选项，我们需要找出符合条件的数列。由于题目描述不完整，假设题目要求的是找到一个数列的最小正周期 $$T$$ 对应的选项。
我们逐一分析选项：
选项A：672
如果数列的周期是672，那么数列每672项重复一次。但题目没有给出具体的数列形式，无法直接验证。
选项B：673
同理，如果周期是673，数列每673项重复一次。同样缺乏具体信息。
选项C：1344
周期为1344的数列每1344项重复一次。
选项D：1345
周期为1345的数列每1345项重复一次。
由于题目描述不完整，无法直接推导出正确答案。但根据常见的题目设计，可能需要计算选项中的数值是否满足某种条件。例如，若数列的周期是某个数的因数，可以验证：
假设数列的周期 $$T$$ 是6的倍数，那么672（$$=6 \times 112$$）和1344（$$=6 \times 224$$）是可能的候选。而673和1345不是6的倍数，可能不符合条件。
进一步，如果题目隐含要求最小周期，672比1344更小，因此选项A更可能正确。
综上所述，最可能正确的答案是：
$$ \boxed{A} $$
题目来源于各渠道收集，若侵权请联系下方邮箱