正确率60.0%无穷等比数列$${{\{}{{a}_{n}}{\}}}$$中,$$^\omega a_{1} > a_{2} "$$是$${{“}}$$数列$${{\{}{{a}_{n}}{\}}}$$为递减数列$${{”}}$$的$${{(}{)}}$$
C
A.充分而不必要条件
B.充分必要条件
C.必要而不充分条件
D.既不充分也不必要条件
2、['数列的函数特征', '数列的通项公式', '等差数列的性质']正确率40.0%记数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}{,}}$$且$$S_{5}=\frac{9} {8},$$数列$${{\{}{{2}^{n}{{S}_{n}}}{\}}}$$是公差为$${{7}}$$的等差数列,则$${{\{}{{a}_{n}}{\}}}$$的最小项为()
C
A.$${{−}{2}}$$
B.$$- \frac{1 5} {1 6}$$
C.$${{−}{1}}$$
D.$$\frac{1} {4}$$
3、['数列的递推公式', '数列的函数特征', '累加法求数列通项', '数列与不等式的综合问题']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的首项为$${{a}_{1}}$$,且$$\left( 1+\frac{1} {n} \right) a_{n-1}-a_{n}=1 \left( n \in\mathbf{N^{*}} \right)$$,若$${{a}_{n}{⩾}{{a}_{4}}}$$,则$${{a}_{1}}$$的取值范围是()
C
A.$$[ \frac{9} {2}, \frac{2 5} {2} ]$$
B.$$[ \frac{4 9} {8}, \frac{8 1} {8} ]$$
C.$$[ 6, 1 0 ]$$
D.$$\left[ \frac{2 5} {4}, 9 \right]$$
4、['数列的递推公式', '数列的函数特征']正确率60.0%在数列$${{\{}{{a}_{n}}{\}}}$$中,$$a_{1}=-2, \ a_{n+1}=1-\frac{1} {a_{n}}$$,则$$a_{2 0 1 8}$$的值为()
D
A.$${{−}{2}}$$
B.$$\frac{1} {3}$$
C.$$\frac{1} {2}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
5、['数列的递推公式', '数列的函数特征']正确率60.0%若数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{n+1}=\left\{\begin{aligned} {} & {{} 2 a_{n}, 0 \leqslant a_{n} < \frac{1} {2},} \\ {} & {{} 2 a_{n}-1, \frac{1} {2} \leqslant a_{n} < 1} \\ \end{aligned} \right.$$若$$a_{1}=\frac{6} {7}$$,则$$a_{2 0}$$的值为$${{(}{)}}$$
B
A.$$\begin{array} {c} {6} \\ {\frac{7} {}} \\ \end{array}$$
B.$$\begin{array} {l l} {5} \\ {\frac{5} {7}} \\ \end{array}$$
C.$$\begin{array} {l l} {\frac{3} {7}} \\ \end{array}$$
D.$$\frac{1} {7}$$
6、['数列的函数特征', '等差数列的基本量', '数列的通项公式']正确率60.0%等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,若$$a_{1}=-2 1, \, \, a_{3}=-1 5$$,则$${{S}_{n}}$$的最小值是()
D
A.$${{−}{{7}{5}}}$$
B.$${{−}{{7}{8}}}$$
C.$${{−}{{8}{1}}}$$
D.$${{−}{{8}{4}}}$$
7、['数列的递推公式', '数列的函数特征', '裂项相消法求和']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=\frac{3} {2}, \, \, a_{n+1}=a_{n}^{2}-a_{n}+1 \, ( n \in N^{*} )$$,则$$m=\frac1 {a_{1}}+\frac1 {a_{2}}+\frac1 {a_{3}}+\cdots+\frac1 {a_{2 0 1 2}}$$的整数部分是
C
A.$${{3}}$$
B.$${{2}}$$
C.$${{1}}$$
D.$${{0}}$$
8、['数列的函数特征', '等比数列的通项公式', '等比数列的定义与证明', '分段函数的单调性']正确率19.999999999999996%已知数列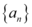 满足
满足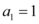 ,
,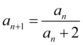
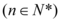 ,若
,若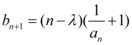 ,
,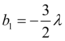 ,且数列
,且数列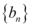 是递增数列,则实数
是递增数列,则实数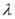 的取值范围为$${{(}{)}}$$
的取值范围为$${{(}{)}}$$
A
A.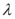
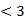
B.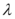
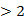
C.
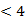
D.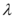
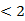
正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,数列$$\{\frac{1} {a_{n}} \}$$的前$${{n}}$$项和为$${{T}_{n}}$$,且$$a_{1}=1, \ a_{2}+a_{3}=1 2, \ S_{n}=\frac{1} {2} ( a_{n+1}-1 )$$,则使得$$| T_{n}-\frac{3} {2} | < \frac{1} {5 0 0}$$成立的$${{n}}$$的最小值为()
D
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}}$$
10、['数列的函数特征', '等差数列的前n项和的应用']正确率80.0%已知等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,$$a_{4}+a_{7}+a_{1 0}=9$$,$$S_{1 4}-S_{3}=7 7$$,则使$${{S}_{n}}$$取得最小值时$${{n}}$$的值为$${{(}{)}}$$
B
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}}$$
以下是各题的详细解析:
.jpg)