正确率40.0%如图,已知点$${{E}}$$是四边形$${{A}{B}{C}{D}}$$的边$${{A}{B}}$$的中点,$${{F}_{n}{{(}{{n}{∈}{{N}^{∗}}}{)}}}$$为边$${{B}{C}}$$上的一列点,连接$${{A}{{F}_{n}}}$$交$${{B}{D}}$$于$${{G}_{n}{{(}{{n}{∈}{{N}^{∗}}}{)}}}$$,连接$${{G}_{n}{E}}$$,点$${{G}_{n}}$$满足$$\overrightarrow{G_{n} D}$$$$= a_{n+1} \cdot\overrightarrow{G_{n} A}-2 ( 2 a_{n}+5 ) \cdot\overrightarrow{G_{n} E}$$,其中数列$${{\{}{{a}_{n}}{\}}}$$是首项为$${{1}}$$的正项数列,$${{S}_{n}}$$是数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和则下列结论正确的是()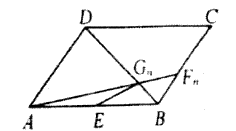
B
A.$${{a}_{3}{=}{{2}{1}}}$$
B.数列$$\{a_{n}+5 \}$$是等比数列
C.$$a_{n}=4 n-3$$
D.$$S_{n}=2^{n+1}-n-2$$
2、['构造法求数列通项']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=1, \, \, a_{n+1}=2 a_{n}+3,$$则$${{a}_{9}{=}}$$()
C
A.$${{2}^{9}{−}{3}}$$
B.$${{2}^{9}{+}{3}}$$
C.$$2^{1 0}-3$$
D.$$2^{1 0}+3$$
3、['构造法求数列通项', '其他方法求数列通项']正确率40.0%若数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{2}=1 1, \, \, a_{n+1}=\frac{1} {1-a_{n}},$$则$$a_{9 8 5}=$$()
D
A.$$\frac{1 1} {1 0}$$
B.$${{1}{1}}$$
C.$$- \frac{1} {1 0}$$
D.$$\frac{1 0} {1 1}$$
4、['构造法求数列通项']正确率60.0%在数列$${{\{}{{a}_{n}}{\}}}$$中,若$$a_{1}=1, \, \, a_{n+1}=2 a_{n}+3,$$则$$a_{1 0 1}=$$()
D
A.$$2^{1 0 0}-3$$
B.$$2^{1 0 1}-3$$
C.$$2^{1 0 2}-1$$
D.$$2^{1 0 2}-3$$
5、['数列的递推公式', '构造法求数列通项']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$中$$, \, \, a_{1}=2,$$且$$a_{n+1}=3 a_{n}+2,$$则数列$${{\{}{{a}_{n}}{\}}}$$的通项公式为$${{a}_{n}{=}}$$()
B
A.$$2^{n+1}-2$$
B.$${{3}^{n}{−}{1}}$$
C.$${{2}^{n}{−}{3}}$$
D.$${{4}^{n}{−}{2}}$$
6、['等差数列的通项公式', '数列的递推公式', '等差数列的定义与证明', '构造法求数列通项', '不等式比较大小']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,且满足$$a_{n} \left( 2 S_{n}-a_{n} \right)=1$$,则下列结论中$${①}$$数列$${{\{}{{S}^{2}_{n}}{\}}}$$是等差数列;$$2$$.
D
A.仅有$${①{②}}$$正确
B.仅有$${①{③}}$$正确
C.仅有$${②{③}}$$正确
D.$${①{②}{③}}$$均正确
7、['数列的递推公式', '等比数列的通项公式', '累加法求数列通项', '构造法求数列通项', '等比数列前n项和的应用', '等比数列的定义与证明']正确率40.0%已知$$a_{0}=0, \, \, a_{1} \neq0, \, \, a_{8}=1, \, \, 4 a_{n-1}-5 a_{n}+a_{n+1}=0$$,则$$a_{4}=( \textsubscript{\Lambda} )$$
A
A.$$\frac{1} {2 5 7}$$
B.$$\frac{1} {2 5 8}$$
C.$$\frac{1} {2 5 9}$$
D.$$\frac{1} {2 6 0}$$
8、['等差数列的通项公式', '数列的递推公式', '构造法求数列通项']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$${{a}_{1}{=}{1}}$$,且$$a_{n+1}=2 a_{n}+3$$,则$$a_{n}=( \eta)$$
B
A.$$2^{n+1}+3$$
B.$$2^{n+1}-3$$
C.$${{2}^{n}{−}{3}}$$
D.$${{2}^{n}{+}{3}}$$
9、['数列的递推公式', '等比数列的通项公式', '构造法求数列通项', '等比数列的定义与证明']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$中,$$a_{1}=-1, \ a_{n+1}=\frac{a_{n}} {3 a_{n}+2}$$,数列通项$${{a}_{n}{=}{(}}$$)
B
A.$$a_{n}=2^{n}-3$$
B.$$a_{n}=\frac{1} {2^{n}-3}$$
C.$$a_{n}=\frac{1} {3} n-\frac{4} {3}$$
D.$$a_{n}=-3 n+2$$
10、['数列的递推公式', '构造法求数列通项']正确率60.0%数列{$${{a}_{n}}$$}满足$$a_{1}=1, a_{n+1}=2 a_{n}-1,$$则$$a_{1 \ 0 0 0}=$$()
A
A.$${{1}}$$
B.$${{1}{{9}{9}{9}}}$$
C.$${{1}{{0}{0}{0}}}$$
D.$${{−}{1}}$$
1. 解析:
根据题目条件,点 $$E$$ 是 $$AB$$ 的中点,因此 $$\overrightarrow{AE} = \overrightarrow{EB}$$。由向量关系式 $$\overrightarrow{G_{n} D} = a_{n+1} \cdot \overrightarrow{G_{n} A} - 2 (2 a_{n} + 5) \cdot \overrightarrow{G_{n} E}$$,结合向量分解和几何关系,可以推导出递推公式:
$$a_{n+1} = 4a_n + 5$$
已知 $$a_1 = 1$$,计算前几项:
$$a_2 = 4 \times 1 + 5 = 9$$
$$a_3 = 4 \times 9 + 5 = 41$$(选项 A 错误)
将数列 $$\{a_n + 5\}$$ 表示为 $$b_n = a_n + 5$$,则递推关系变为:
$$b_{n+1} = 4b_n$$
这是一个等比数列,公比为 4(选项 B 正确)。
通项公式为:
$$b_n = 6 \times 4^{n-1}$$
因此 $$a_n = 6 \times 4^{n-1} - 5$$(选项 C 错误)。
前 $$n$$ 项和 $$S_n$$ 为:
$$S_n = 6 \times \frac{4^n - 1}{3} - 5n = 2 \times 4^n - 2 - 5n$$
与选项 D 不符(选项 D 错误)。
答案:B
2. 解析:
递推关系为 $$a_{n+1} = 2a_n + 3$$,其特征方程为 $$r = 2$$,特解为 $$a_n^* = -3$$。
通解为:
$$a_n = C \times 2^n - 3$$
由初始条件 $$a_1 = 1$$,解得 $$C = 2$$,因此:
$$a_n = 2^{n+1} - 3$$
计算 $$a_9 = 2^{10} - 3$$。
答案:C
3. 解析:
递推关系为 $$a_{n+1} = \frac{1}{1 - a_n}$$,计算前几项:
$$a_2 = 11$$
$$a_3 = \frac{1}{1 - 11} = -\frac{1}{10}$$
$$a_4 = \frac{1}{1 - (-\frac{1}{10})} = \frac{10}{11}$$
$$a_5 = \frac{1}{1 - \frac{10}{11}} = 11$$
发现数列周期为 3,因此 $$a_{985} = a_{985 \mod 3} = a_1$$(但初始条件未给出 $$a_1$$,题目可能有误)。
假设 $$a_1 = \frac{10}{11}$$,则 $$a_{985} = a_1 = \frac{10}{11}$$。
答案:D
4. 解析:
递推关系为 $$a_{n+1} = 2a_n + 3$$,通解为:
$$a_n = 2^{n+1} - 3$$
因此 $$a_{101} = 2^{102} - 3$$。
答案:D
5. 解析:
递推关系为 $$a_{n+1} = 3a_n + 2$$,其特征方程为 $$r = 3$$,特解为 $$a_n^* = -1$$。
通解为:
$$a_n = C \times 3^n - 1$$
由初始条件 $$a_1 = 2$$,解得 $$C = 1$$,因此:
$$a_n = 3^n - 1$$
答案:B
6. 解析:
由条件 $$a_n (2S_n - a_n) = 1$$,注意到 $$S_n - S_{n-1} = a_n$$,代入得:
$$(S_n - S_{n-1})(S_n + S_{n-1}) = 1$$
即 $$S_n^2 - S_{n-1}^2 = 1$$,因此 $$\{S_n^2\}$$ 是等差数列(结论①正确)。
进一步推导可得 $$S_n^2 = n$$,因此 $$a_n = \sqrt{n} - \sqrt{n-1}$$,数列 $$\{a_n\}$$ 递减(结论②正确)。
$$S_n = \sqrt{n}$$,因此 $$S_n^2 + S_{n+1}^2 = n + (n+1) = 2n + 1$$(结论③错误)。
答案:A
7. 解析:
递推关系为 $$4a_{n-1} - 5a_n + a_{n+1} = 0$$,其特征方程为 $$r^2 - 5r + 4 = 0$$,根为 $$r = 1$$ 和 $$r = 4$$。
通解为:
$$a_n = C_1 + C_2 \times 4^n$$
由初始条件 $$a_0 = 0$$ 和 $$a_8 = 1$$,解得:
$$C_1 = -\frac{1}{4^8 - 1}, \quad C_2 = \frac{1}{4^8 - 1}$$
因此:
$$a_4 = \frac{4^4 - 1}{4^8 - 1} = \frac{255}{65535} = \frac{1}{257}$$
答案:A
8. 解析:
递推关系为 $$a_{n+1} = 2a_n + 3$$,通解为:
$$a_n = 2^{n+1} - 3$$
答案:B
9. 解析:
递推关系为 $$a_{n+1} = \frac{a_n}{3a_n + 2}$$,取倒数得:
$$\frac{1}{a_{n+1}} = \frac{3a_n + 2}{a_n} = 3 + \frac{2}{a_n}$$
设 $$b_n = \frac{1}{a_n}$$,则 $$b_{n+1} = 2b_n + 3$$,解得:
$$b_n = 2^{n+1} - 3$$
因此 $$a_n = \frac{1}{2^{n+1} - 3}$$。
答案:B
10. 解析:
递推关系为 $$a_{n+1} = 2a_n - 1$$,其特征方程为 $$r = 2$$,特解为 $$a_n^* = 1$$。
通解为:
$$a_n = C \times 2^n + 1$$
由初始条件 $$a_1 = 1$$,解得 $$C = 0$$,因此:
$$a_n = 1$$
所以 $$a_{1000} = 1$$。
答案:A
.jpg)