.jpg)
正确率60.0%小张在乘坐某条线路的地铁时，从起点站开始，利用手机上的里程表测出前两站的距离大约为$${{2}}$$千米，以后每经过一站里程约增加$${{0}{.}{1}}$$千米，已知此条地铁线路的总行程大约为$${{5}{1}{.}{3}}$$千米，据此他测算出此条地铁线路的站点(含起始站与终点站)数为（）
B
A.$${{1}{8}}$$
B.$${{1}{9}}$$
C.$${{2}{1}}$$
D.$${{2}{2}}$$
2、['数列在日常经济生活中的应用'， '等差模型'， '等差数列的前n项和的应用']正确率60.0%根据科学计算，某运载飞船的火箭点火$${{1}}$$分钟内通过的路程为$${{2}}$$千米，以后每分钟通过的路程增加$${{2}}$$千米，在到达离地面$${{2}{4}{0}}$$千米的高度时，火箭与飞船分离，则这一过程需要的时间是（）
C
A.$${{1}{0}}$$分钟
B.$${{1}{3}}$$分钟
C.$${{1}{5}}$$分钟
D.$${{2}{0}}$$分钟
3、['等差数列的通项公式'， '等差模型'， '数列中的数学文化问题']正确率60.0%若冬至、小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影长依次成等差数列，冬至、立春、春分的日影长之和为$${{3}{1}{.}{5}}$$尺，前九个节气的日影长之和为$${{8}{5}{.}{5}}$$尺，则小满的日影长为（）
C
A.$${{1}{.}{5}}$$尺
B.$${{2}{.}{5}}$$尺
C.$${{3}{.}{5}}$$尺
D.$${{4}{.}{5}}$$尺
4、['等差模型'， '数列中的数学文化问题']正确率60.0%南宋数学家杨辉所著的《详解九章算法》中有如图所示的几何体，后人称之为“三角垛”.“三角垛”的最上层有$${{1}}$$个球，第二层有$${{3}}$$个球，第三层有$${{6}}$$个球，…，则第十层球的个数为（）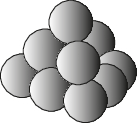
B
A.$${{4}{5}}$$
B.$${{5}{5}}$$
C.$${{9}{0}}$$
D.$${{1}{1}{0}}$$
5、['等差模型'， '等差数列的前n项和的应用']正确率80.0%《张邱建算经》记载：今有女子不善织布，逐日织布同数递减，初日织五尺，末一日织一尺，计织三十日，问共织布$${{(}{)}{.}}$$
C
A.$${{1}{8}{0}}$$尺
B.$${{1}{1}{0}}$$尺
C.$${{9}{0}}$$尺
D.$${{6}{0}}$$尺
6、['等差模型'， '等差数列的前n项和的应用']正确率80.0%古代数学名著《张丘建算经》中曾出现过高息借贷的题目：“今有举取他绢，重作券；要过限一日，息绢一尺；二日息二尺；如是息绢日多一尺．今过限一百日，问息绢几何？”题目的意思是：债主拿欠债方的绢做抵押品，每过期一天便加纳一天利息，债务过期一天要纳利息一尺绢，过期二天则第二天便再纳利息二尺，这样，每天利息比前一天增加一尺．若过期$${{1}{0}{0}}$$天，欠债方共纳利息为$${{(}{)}}$$
D
A.$${{1}{0}{0}}$$尺
B.$${{4}{9}{5}{0}}$$尺
C.$${{5}{0}{0}{0}}$$尺
D.$${{5}{0}{5}{0}}$$尺
7、['等差数列的通项公式'， '等差模型']正确率40.0%北京天坛的圆丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板（称为天心石），环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板（不含天心石）( )
A.3699块
B.3474块
C.3402块
D.3339块
8、['等差模型']正确率40.0%
已知从$${{1}}$$开始的连续奇数蛇形排列形成宝塔形数表，第一行为$${{1}}$$，第二行为$${{3}}$$，$${{5}}$$，第三行为$${{7}}$$，$${{9}}$$，$${{1}{1}}$$，第四行为$${{1}{3}}$$，$${{1}{5}}$$，$${{1}{7}}$$，$${{1}{9}}$$，如图所示，在宝塔形数表中位于第$${{i}}$$行，第$${{j}}$$列的数记为$$a_{i， j}$$，比如$$a_{3， 2}=9$$，$$a_{4， 2}=1 5$$，$$a_{5， 4} \，=2 3$$，若$$a_{i， j}=2 0 1 7$$，则$$i+j=( \begin{array} {c} {} \\ {} \\ \end{array} )$$
D
A.$${{6}{4}}$$
B.$${{6}{5}}$$
C.$${{7}{1}}$$
D.$${{7}{2}}$$
9、['等差数列的通项公式'， '等差模型']正确率80.0%《周髀算经》中一个问题：从冬至之日起，小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影子长依次成等差数列，若冬至、立春、春分的日影子长的和是$${{3}{7}{.}{5}}$$尺，芒种的日影子长为$${{4}{.}{5}}$$尺，则冬至的日影子长为$${{(}{)}}$$
A
A.$${{1}{5}{.}{5}}$$尺
B.$${{1}{2}{.}{5}}$$尺
C.$${{1}{0}{.}{5}}$$尺
D.$${{9}{.}{5}}$$尺
10、['等差模型'， '等差数列的前n项和的应用']正确率80.0%《算法统宗》是中国古代数学名著，由明代数学家程大位编著，它对我国民间普及珠算和数学知识起到了很大的作用，是东方古代数学的名著，在这部著作中，许多数学问题都是以歌诀形式呈现的$${{.}}$$“九儿问甲歌”就是其中一首：一个公公九个儿，若问生年总不知，自长排来差三岁，共年二百又零七，借问小儿多少岁，各儿岁数要谁推，这位公公年龄最小的儿子年龄为$${{(}{)}}$$
B
A.$${{8}}$$岁
B.$${{1}{1}}$$岁
C.$${{2}{0}}$$岁
D.$${{3}{5}}$$岁
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.