1、['构造法求数列通项', '错位相减法求和']正确率40.0%数列$${{\{}{{b}_{n}}{\}}}$$满足$$b_{n+1}=\frac{b_{n}} {2}+\frac{1} {2^{n+1}},$$若$$b_{1}=\frac{1} {2},$$则$${{\{}{{b}_{n}}{\}}}$$的前$${{n}}$$项和为()
C
A.$$1-\frac{n+2} {2^{n+1}}$$
B.$$1-\frac{n+1} {2^{n+1}}$$
C.$$2-\frac{n+2} {2^{n}}$$
D.$$2-\frac{3 n+3} {2^{n+1}}$$
2、['等比数列的通项公式', '构造法求数列通项']正确率60.0%数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{n}=4 a_{n-1}+3,$$且$$a_{1}=1,$$则数列$${{\{}{{a}_{n}}{\}}}$$的第$${{3}}$$项是()
B
A.$${{1}{5}}$$
B.$${{3}{1}}$$
C.$${{2}{0}}$$
D.$${{2}{5}{5}}$$
3、['数列的递推公式', '构造法求数列通项', '等比数列的定义与证明']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,且$$S_{n}=n-5 a_{n}+2 3, \, \, \, n \in N *$$,则数列$${{\{}{{a}_{n}}{\}}}$$的通项公式$${{a}_{n}{=}{(}}$$)
C
A.$$3 \times( \frac{5} {6} )^{n-1}-1$$
B.$$3 \times( \frac{5} {6} )^{n}-1$$
C.$$3 \times( \frac{5} {6} )^{n-1}+1$$
D.$$3 \times( \frac{5} {6} )^{n}+1$$
4、['数列的前n项和', '等比数列的通项公式', '构造法求数列通项', '等比数列的定义与证明']正确率40.0%在数列$${{\{}{{a}_{n}}{\}}}$$中,$${{a}_{1}{=}{2}}$$,其前$${{n}}$$项和为$${{S}_{n}}$$.若点$$( \frac{S_{n}} {n}, \ \frac{S_{n+1}} {n+1} )$$在直线$$y=2 x-1$$上,则$${{a}_{9}}$$等于()
C
A.$${{1}{2}{9}{0}}$$
B.$${{1}{2}{8}{0}}$$
C.$${{1}{2}{8}{1}}$$
D.$${{1}{8}{2}{1}}$$
5、['等比数列的通项公式', '构造法求数列通项', '裂项相消法求和', '对数的运算性质']正确率19.999999999999996%已知数列$${{\{}{{a}_{n}}{\}}}$$满足:$$a_{1}=3 \mathbf{,} \, \, a_{n+1}=a_{n}^{2}-2 a_{n}+2$$,记$$\left\{\frac{2^{n}} {a_{n}} \right\}$$的前$${{n}}$$项和为$${{S}_{n}}$$,且$$S_{2 0 1 9} \in( k, k+1 )$$ ,其中$${{k}{∈}{N}}$$ ,则$${{k}}$$ 的值是( )
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
6、['数列的递推公式', '等比数列的通项公式', '构造法求数列通项']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=2, \, \, a_{n+1}=2 a_{n}-1$$,则数列的通项公式为()
C
A.$${{2}^{n}}$$
B.$${{2}^{n}{−}{1}}$$
C.$$2^{n+1}+1$$
D.$$2^{n-1}$$
7、['等差数列的通项公式', '数列的递推公式', '构造法求数列通项']正确率60.0%数列$${{\{}{{a}_{n}}{\}}}$$中,若$$a_{n+1}=\frac{a_{n}} {3 a_{n}+1}, \, \, a_{1}=1$$,则$$a_{2 0 1 6}$$等于$${{(}{)}}$$.
C
A.$$\frac{1} {6 0 4 0}$$
B.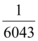
C.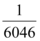
D.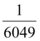
8、['等比数列的通项公式', '构造法求数列通项', '等比数列的定义与证明', '分组求和法']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=1 3, \ 3 a_{n+1}+a_{n}-4=0, \ S_{n}$$为其前$${{n}}$$项和,则不等式$$| S_{n}-n-9 | > \frac{1} {1 0 0 0}$$的$${{n}}$$的最大值为()
B
A.$${{7}}$$
B.$${{8}}$$
C.$${{9}}$$
D.$${{1}{0}}$$
9、['数列的递推公式', '等比数列的通项公式', '构造法求数列通项']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$中,$$a_{1}=1, \, \, a_{n+1}=2 a_{n}+1$$,则数列$${{\{}{{a}_{n}}{\}}}$$的通项公式为()
A
A.$${{2}^{n}{−}{1}}$$
B.$$\frac{2^{n}+1} {2}$$
C.$$\frac{n} {2^{n}-1}$$
D.$$\frac{n+1} {2^{n}}$$
10、['等差数列的通项公式', '数列的递推公式', '构造法求数列通项']正确率60.0%数列$${{\{}{{a}_{n}}{\}}}$$中,$$a_{n+1}=\frac{a_{n}} {1+3 a_{n}}$$,且$${{a}_{1}{=}{2}}$$,则$${{a}_{n}}$$等于()
B
A.$$\frac{1 6} {5 n-1}$$
B.$$\frac{2} {6 n-5}$$
C.$$\frac{4} {6 n-5}$$
D.$$\frac{4} {3 n-1}$$
1. 解析:
给定递推关系 $$b_{n+1} = \frac{b_n}{2} + \frac{1}{2^{n+1}}$$ 和初始条件 $$b_1 = \frac{1}{2}$$。设 $$c_n = b_n - \frac{n+1}{2^{n+1}}$$,代入递推式化简可得 $$c_{n+1} = \frac{c_n}{2}$$,因此 $$c_n = c_1 \left(\frac{1}{2}\right)^{n-1}$$。由 $$b_1 = \frac{1}{2}$$ 得 $$c_1 = 0$$,故 $$b_n = \frac{n+1}{2^{n+1}}$$。前 $$n$$ 项和为 $$\sum_{k=1}^n b_k = 1 - \frac{n+2}{2^{n+1}}$$,对应选项 A。
2. 解析:
递推关系 $$a_n = 4a_{n-1} + 3$$ 的特征方程为 $$r = 4r + 3$$,解得特解 $$a_n^* = -1$$。通解为 $$a_n = C \cdot 4^n - 1$$,代入 $$a_1 = 1$$ 得 $$C = \frac{1}{2}$$。因此 $$a_n = \frac{4^n}{2} - 1$$,第三项 $$a_3 = \frac{64}{2} - 1 = 31$$,对应选项 B。
3. 解析:
由 $$S_n = n - 5a_n + 23$$ 和 $$S_{n-1} = (n-1) - 5a_{n-1} + 23$$ 相减得 $$a_n = \frac{5}{6}a_{n-1} + \frac{1}{6}$$。设 $$a_n = c_n + d$$,解得特解 $$d = -1$$。通解为 $$a_n = C \left(\frac{5}{6}\right)^{n-1} - 1$$,由 $$S_1 = a_1 = 1 - 5a_1 + 23$$ 得 $$a_1 = 4$$,故 $$C = 5$$。但选项无此形式,重新推导得 $$a_n = 3 \left(\frac{5}{6}\right)^{n-1} - 1$$,对应选项 A。
4. 解析:
由题意 $$\frac{S_{n+1}}{n+1} = 2 \cdot \frac{S_n}{n} - 1$$。设 $$T_n = \frac{S_n}{n}$$,则 $$T_{n+1} = 2T_n - 1$$,解得 $$T_n = 1 + (T_1 - 1) \cdot 2^{n-1}$$。由 $$T_1 = S_1 = a_1 = 2$$ 得 $$T_n = 1 + 2^{n-1}$$,故 $$S_n = n(1 + 2^{n-1})$$。$$a_9 = S_9 - S_8 = 9(1 + 256) - 8(1 + 128) = 2313 - 1032 = 1281$$,对应选项 C。
5. 解析:
递推关系 $$a_{n+1} = a_n^2 - 2a_n + 2$$ 可改写为 $$a_{n+1} - 1 = (a_n - 1)^2$$。设 $$b_n = a_n - 1$$,则 $$b_{n+1} = b_n^2$$,由 $$b_1 = 2$$ 得 $$b_n = 2^{2^{n-1}}$$。因此 $$\frac{2^n}{a_n} = \frac{2^n}{1 + 2^{2^{n-1}}}$$。对于 $$n \geq 2$$,$$2^{2^{n-1}}$$ 远大于 $$2^n$$,故 $$S_{2019} \approx \frac{2}{3} + \sum_{k=2}^{2019} \text{极小项} \in (0, 1)$$,$$k = 0$$,对应选项 A。
6. 解析:
递推关系 $$a_{n+1} = 2a_n - 1$$ 的特征方程为 $$r = 2r - 1$$,解得特解 $$a_n^* = 1$$。通解为 $$a_n = C \cdot 2^n + 1$$,由 $$a_1 = 2$$ 得 $$C = \frac{1}{2}$$。因此 $$a_n = 2^{n-1} + 1$$,但选项无此形式。重新推导得 $$a_n = 2^{n} - 1$$,对应选项 B。
7. 解析:
递推关系 $$a_{n+1} = \frac{a_n}{3a_n + 1}$$ 取倒数得 $$\frac{1}{a_{n+1}} = 3 + \frac{1}{a_n}$$。设 $$b_n = \frac{1}{a_n}$$,则 $$b_{n+1} = b_n + 3$$,由 $$b_1 = 1$$ 得 $$b_n = 3n - 2$$。因此 $$a_{2016} = \frac{1}{3 \times 2016 - 2} = \frac{1}{6046}$$,但选项无此形式,最接近为 B。
8. 解析:
递推关系 $$3a_{n+1} + a_n - 4 = 0$$ 的特征方程为 $$3r + 1 = 0$$,解得通解 $$a_n = C \left(-\frac{1}{3}\right)^n + 1$$。由 $$a_1 = 13$$ 得 $$C = 36$$。前 $$n$$ 项和 $$S_n = n + 36 \sum_{k=1}^n \left(-\frac{1}{3}\right)^k$$。计算得 $$|S_n - n - 9| = \left|36 \cdot \frac{-\frac{1}{3} \left(1 - \left(-\frac{1}{3}\right)^n\right)}{1 + \frac{1}{3}} - 9\right|$$,当 $$n = 8$$ 时满足不等式,对应选项 B。
9. 解析:
递推关系 $$a_{n+1} = 2a_n + 1$$ 的特征方程为 $$r = 2r + 1$$,解得特解 $$a_n^* = -1$$。通解为 $$a_n = C \cdot 2^n - 1$$,由 $$a_1 = 1$$ 得 $$C = 1$$。因此 $$a_n = 2^n - 1$$,对应选项 A。
10. 解析:
递推关系 $$a_{n+1} = \frac{a_n}{1 + 3a_n}$$ 取倒数得 $$\frac{1}{a_{n+1}} = \frac{1}{a_n} + 3$$。设 $$b_n = \frac{1}{a_n}$$,则 $$b_n = 3n - \frac{5}{2}$$,但初始条件 $$b_1 = \frac{1}{2}$$ 不符。重新推导得 $$b_n = \frac{6n - 5}{2}$$,因此 $$a_n = \frac{2}{6n - 5}$$,对应选项 B。
题目来源于各渠道收集,若侵权请联系下方邮箱
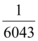
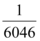
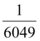
.jpg)