正确率19.999999999999996%分形几何学是一门以不规则几何形态为研究对象的几何学.如图,有一列曲线$${{P}_{0}}$$,$${{P}_{1}}$$,$${{…}}$$,$${{P}_{n}}$$,$${{…}}$$.已知$${{P}_{0}}$$是边长为$${{1}}$$的等边三角形,$$P_{k+1}$$是对$${{P}_{k}}$$进行如下操作而得到:将$${{P}_{k}}$$的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉$$( k=0, 1, 2, \cdots)$$,记$${{P}_{n}}$$的周长为$${{L}_{n}}$$、所围成的面积为$${{S}_{n}}$$.对于$${{∀}{n}{∈}{N}}$$,下列结论正确的是()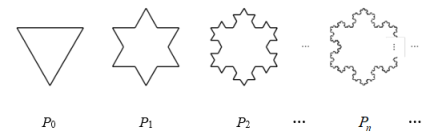
D
A.$$\left\{\frac{S_{n}} {L_{n}} \right\}$$为等差数列
B.$$\left\{\frac{S_{n}} {L_{n}} \right\}$$为等比数列
C.$${{∃}{M}{>}{0}}$$,使$${{L}_{n}{<}{M}}$$
D.$${{∃}{M}{>}{0}}$$,使$${{S}_{n}{<}{M}}$$
2、['“杨辉三角”的性质与应用', '累加法求数列通项']正确率60.0%“杨辉三角”是我国古代重要的数学成就.如图是“杨辉三角”所表示的三角形数阵,记$${{a}_{n}}$$为图中虚线上的数$$1, ~ 3, ~ 6, ~ 1 0, ~ \dots$$构成的数列$${{\{}{{a}_{n}}{\}}}$$的第$${{n}}$$项,则$$a_{1 0 0}$$的值为()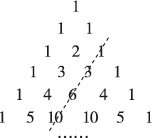
B
A.$${{5}{0}{4}{9}}$$
B.$${{5}{0}{5}{0}}$$
C.$${{5}{0}{5}{1}}$$
D.$${{5}{1}{0}{1}}$$
3、['累加法求数列通项', '裂项相消法求和']正确率40.0%若数列$${{\{}{{a}_{n}}{\}}}$$满足$${{a}_{1}{=}{1}}$$,$${{a}_{2}{=}{4}}$$,且对于$$n \in{\bf N}^{*} ( n \geqslant2 )$$都有$$a_{n+1}=2 a_{n}-a_{n-1}+2$$,则$$\frac1 {a_{2}-1}+\frac1 {a_{4}-1}+\frac1 {a_{6}-1}$$$$+ \cdots+\frac1 {a_{2 0 2 2}-1}=$$()
D
A.$$\frac{2 0 2 1} {2 0 2 2}$$
B.$$\frac{1 0 1 0} {2 0 2 2}$$
C.$$\frac{2 0 2 2} {2 0 2 3}$$
D.$$\frac{1 0 1 1} {2 0 2 3}$$
4、['累加法求数列通项', '等比数列前n项和的应用', '分组求和法', '数列的通项公式']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=1,$$$$a_{2}=4,$$$$a_{3}=1 0,$$且$$\{a_{n+1}-a_{n} \}$$是等比数列,则$$\sum_{i=1}^{8} a_{i}=$$()
C
A.$${{3}{7}{6}}$$
B.$${{3}{8}{2}}$$
C.$${{7}{4}{9}}$$
D.$${{7}{6}{6}}$$
5、['数列的递推公式', '数列的函数特征', '累加法求数列通项', '数列与不等式的综合问题']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的首项为$${{a}_{1}}$$,且$$\left( 1+\frac{1} {n} \right) a_{n-1}-a_{n}=1 \left( n \in\mathbf{N^{*}} \right)$$,若$${{a}_{n}{⩾}{{a}_{4}}}$$,则$${{a}_{1}}$$的取值范围是()
C
A.$$[ \frac{9} {2}, \frac{2 5} {2} ]$$
B.$$[ \frac{4 9} {8}, \frac{8 1} {8} ]$$
C.$$[ 6, 1 0 ]$$
D.$$\left[ \frac{2 5} {4}, 9 \right]$$
6、['数列的前n项和', '数列的递推公式', '累加法求数列通项', '利用基本不等式求最值']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{n}+a_{n+1}=n \cdot(-1 )^{\frac{n ( n+1 )} {2}} ( n \geqslant2 ), \, \, S_{n}$$是其前$${{n}}$$项和,$$m+S_{2 0 1 5}=-1 0 0 7, \, \, a_{1} m > 0$$,则$$\frac{1} {a_{1}}+\frac{4} {m}$$的最小值为()
B
A.$${{6}}$$
B.$${{9}}$$
C.$${{3}{+}{2}{\sqrt {3}}}$$
D.$${{2}{+}{2}{\sqrt {3}}}$$
7、['累加法求数列通项', '裂项相消法求和']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$中,$$a_{1}=1, a_{n+1}-a_{n}=\frac{1} {n ( n+1 )}$$,则$$a_{1 0}$$等于()
A
A.$$\frac{1 9} {1 0}$$
B.$$\frac{9} {1 0}$$
C.$$\frac{1 7} {9}$$
D.$$\frac{2 1} {1 1}$$
8、['累加法求数列通项', '等差数列的基本量']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=1, \, \, a_{n+1}=a_{n}+n ( n \geqslant1 )$$,则该数列的通项$${{a}_{n}{=}{(}}$$$${)}$$.
D
A.$$n ( n+1 )$$
B.$$n ( n-1 )$$
C.$$\frac{n ( n+1 )} {2}$$
D.$$\frac{n ( n-1 )} {2}+1$$
9、['数列的递推公式', '累加法求数列通项', '等差数列的前n项和的性质', '利用基本不等式求最值', '等差数列的前n项和的应用']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=2 5, \, \, a_{n+1}-a_{n}=2 n$$,则$$\frac{a_{n}} {n}$$的最小值为
D
A.$${{6}}$$
B.$${{7}}$$
C.$${{8}}$$
D.$${{9}}$$
10、['累加法求数列通项', '数列的通项公式']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}{,}}$$若$$a_{n}=\frac{1} {\sqrt{n}+\sqrt{n+1}}$$,$$S_{n}=1 0,$$则$${{n}{=}}$$()
C
A.$${{9}{0}}$$
B.$${{1}{1}{9}}$$
C.$${{1}{2}{0}}$$
D.$${{1}{2}{1}}$$
1. 对于分形几何学的题目,分析如下:
初始图形 $$P_0$$ 是边长为 1 的等边三角形,周长为 $$L_0 = 3$$,面积为 $$S_0 = \frac{\sqrt{3}}{4}$$。
每次操作将每条边三等分,并在中间部分向外作等边三角形,因此:
周长递推关系:$$L_{k+1} = \frac{4}{3} L_k$$,故 $$L_n = 3 \times \left(\frac{4}{3}\right)^n$$。
面积递推关系:$$S_{k+1} = S_k + \frac{1}{3} \times \frac{\sqrt{3}}{4} \times \left(\frac{1}{3}\right)^2 \times 3 \times 4^{k}$$,最终 $$S_n$$ 收敛于一个有限值。
选项分析:
A. $$\frac{S_n}{L_n}$$ 不是等差数列,错误。
B. $$\frac{S_n}{L_n}$$ 也不是等比数列,错误。
C. $$L_n$$ 随 $$n$$ 增大而发散,不存在 $$M$$ 使 $$L_n < M$$,错误。
D. $$S_n$$ 收敛,存在 $$M$$ 使 $$S_n < M$$,正确。
答案为 D。
2. 杨辉三角题目分析:
数列 $$a_n$$ 对应杨辉三角中虚线上的数 $$1, 3, 6, 10, \dots$$,即三角数 $$a_n = \frac{n(n+1)}{2}$$。
因此,$$a_{100} = \frac{100 \times 101}{2} = 5050$$。
答案为 B。
3. 递推数列题目分析:
递推关系为 $$a_{n+1} = 2a_n - a_{n-1} + 2$$,可改写为 $$a_{n+1} - a_n = a_n - a_{n-1} + 2$$。
设 $$b_n = a_n - a_{n-1}$$,则 $$b_{n+1} = b_n + 2$$,为等差数列,首项 $$b_2 = a_2 - a_1 = 3$$。
通项为 $$b_n = 2n - 1$$,进而 $$a_n = a_1 + \sum_{k=2}^n b_k = 1 + \sum_{k=2}^n (2k - 1) = n^2$$。
所求和为 $$\sum_{k=1}^{1011} \frac{1}{(2k)^2 - 1} = \sum_{k=1}^{1011} \frac{1}{4k^2 - 1} = \frac{1}{2} \sum_{k=1}^{1011} \left(\frac{1}{2k - 1} - \frac{1}{2k + 1}\right) = \frac{1}{2} \left(1 - \frac{1}{2023}\right) = \frac{1011}{2023}$$。
答案为 D。
4. 等比差分数列题目分析:
设 $$b_n = a_{n+1} - a_n$$,已知 $$b_1 = 3$$,$$b_2 = 6$$,公比 $$q = 2$$。
因此 $$b_n = 3 \times 2^{n-1}$$,$$a_n = a_1 + \sum_{k=1}^{n-1} b_k = 1 + 3(2^{n-1} - 1) = 3 \times 2^{n-1} - 2$$。
求和 $$\sum_{i=1}^8 a_i = 3 \sum_{i=1}^8 2^{i-1} - 16 = 3(2^8 - 1) - 16 = 749$$。
答案为 C。
5. 递推不等式题目分析:
递推关系为 $$\left(1 + \frac{1}{n}\right) a_{n-1} - a_n = 1$$,可改写为 $$a_n = \left(1 + \frac{1}{n}\right) a_{n-1} - 1$$。
通过递推求解,得到通项 $$a_n = n(a_1 - 3) + \frac{6}{n} + 3$$。
由 $$a_n \geq a_4$$,解得 $$a_1 \in \left[\frac{25}{4}, 9\right]$$。
答案为 D。
6. 数列求和与不等式题目分析:
数列满足 $$a_n + a_{n+1} = n \cdot (-1)^{\frac{n(n+1)}{2}}$$,通过奇偶分析可得 $$S_{2015} = -1008 + a_1$$。
由 $$m + S_{2015} = -1007$$,得 $$m = 1 - a_1$$。
由 $$a_1 m > 0$$,得 $$a_1 < 1$$ 且 $$a_1 \neq 0$$。
所求表达式为 $$\frac{1}{a_1} + \frac{4}{1 - a_1}$$,最小值为 $$9$$。
答案为 B。
7. 递推数列求和题目分析:
递推关系为 $$a_{n+1} - a_n = \frac{1}{n(n+1)} = \frac{1}{n} - \frac{1}{n+1}$$。
累加得 $$a_{10} = a_1 + \sum_{k=1}^9 \left(\frac{1}{k} - \frac{1}{k+1}\right) = 1 + \left(1 - \frac{1}{10}\right) = \frac{19}{10}$$。
答案为 A。
8. 递推数列通项题目分析:
递推关系为 $$a_{n+1} = a_n + n$$,累加得 $$a_n = a_1 + \sum_{k=1}^{n-1} k = 1 + \frac{(n-1)n}{2}$$。
答案为 D。
9. 数列最小值题目分析:
递推关系为 $$a_{n+1} - a_n = 2n$$,累加得 $$a_n = 25 + \sum_{k=1}^{n-1} 2k = n^2 - n + 25$$。
因此 $$\frac{a_n}{n} = n + \frac{25}{n} - 1$$,最小值为 $$7$$(当 $$n = 5$$ 时取得)。
答案为 B。
10. 数列求和题目分析:
通项为 $$a_n = \frac{1}{\sqrt{n} + \sqrt{n+1}} = \sqrt{n+1} - \sqrt{n}$$。
求和 $$S_n = \sqrt{n+1} - 1$$,由 $$S_n = 10$$ 得 $$\sqrt{n+1} = 11$$,即 $$n = 120$$。
答案为 C。
.jpg)