.jpg)
正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$的通项公式$$a_{n}=n \operatorname{c o s} \frac{n \pi} {2}+1$$，其前$${{n}}$$项和为$${{S}_{n}}$$，则$$S_{2 0 1 2}$$等于$${{(}{)}}$$
D
A.$${{5}{0}{3}}$$
B.$${{1}{0}{0}{6}}$$
C.$${{2}{0}{1}{2}}$$
D.$${{3}{0}{1}{8}}$$
2、['分组求和法'， '直线的斜率']正确率40.0%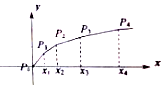
已知在平面直角坐标系中，依次连接点$$P_{1} \ ( 0， \ 0 ) \， \ P_{1} \ ( \ x_{1}， \ 1 ) \， \ P \ ( \ x_{2}， \ 2 ) \ \ldots\ldots P_{n} \ ( \ x_{n}， \ n )$$
A
A.$$2^{n+1}-n-2$$
B.$$2^{n+1}-n$$
C.$$2^{n-1}-n-2$$
D.$$2^{n+1}+n$$
3、['分组求和法']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$$S_{n}， ~ a_{1}=\frac{1} {1 0 1 2}，$$$$a_{n}+a_{n+1}+a_{n+2}=\frac{n+2} {1 0 1 2}，$$则$$S_{2 0 2 3}=$$（）
A
A.$${{6}{7}{5}}$$
B.$${{6}{7}{4}}$$
C.$${{1}{3}{8}{4}}$$
D.$${{2}{0}{2}{3}}$$
4、['分组求和法']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$${{a}_{1}{=}{1}}$$，$$a_{n}+(-1 )^{n} a_{n+1}=1-\frac{n} {2 0 2 2}$$，记数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$，则$$S_{2 0 2 3}=( \textsubscript{\Lambda} )$$
A.$${{5}{0}{6}}$$
B.$${{7}{5}{9}}$$
C.$${{1}{0}{1}{1}}$$
D.$${{1}{0}{1}{2}}$$
5、['累加法求数列通项'， '等比数列前n项和的应用'， '分组求和法'， '数列的通项公式']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=1，$$$$a_{2}=4，$$$$a_{3}=1 0，$$且$$\{a_{n+1}-a_{n} \}$$是等比数列，则$$\sum_{i=1}^{8} a_{i}=$$（）
C
A.$${{3}{7}{6}}$$
B.$${{3}{8}{2}}$$
C.$${{7}{4}{9}}$$
D.$${{7}{6}{6}}$$
6、['数列中的新定义问题'， '分组求和法']正确率40.0%设数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和是$${{S}_{n}}$$，令$$T_{n}=\frac{S_{1}+S_{2}+\cdots+S_{n}} {n}$$，称$${{T}_{n}}$$为数列$${{a}_{1}}$$，$${{a}_{2}}$$，$${{…}}$$，$${{a}_{n}}$$的$${{“}}$$理想数$${{”}}$$，已知数列$${{a}_{1}}$$，$${{a}_{2}}$$，$${{…}}$$，$$a_{5 0 2}$$的$${{“}}$$理想数$${{”}}$$为$${{2}{0}{1}{2}}$$，则数列$${{6}}$$，$${{a}_{1}}$$，$${{a}_{2}}$$，$${{…}}$$，$$a_{5 0 2}$$的理想数为（）
A
A.$${{2}{0}{1}{4}}$$
B.$${{2}{0}{1}{5}}$$
C.$${{2}{0}{1}{6}}$$
D.$${{2}{0}{1}{7}}$$
7、['等差数列的通项公式'， '其他方法求数列通项'， '数列中的新定义问题'， '分组求和法'， '等差数列的前n项和的应用']正确率40.0%对于数列$${{\{}{{a}_{n}}{\}}{，}}$$定义$$A_{n}=\frac{a_{1}+2 a_{2}+\ldots+2^{n-1} a_{n}} {n}$$为数列$${{\{}{{a}_{n}}{\}}}$$的$${{“}}$$诚信$${{”}}$$值，已知某数列$${{\{}{{a}_{n}}{\}}}$$的$${{“}}$$诚信$${{”}}$$值$$A_{n}=2^{n+1}$$，记数列$$\{a_{n}-k n \}$$的前$${{n}}$$项和为$${{S}_{n}}$$，若$${{S}_{n}{⩽}{{S}_{5}}}$$对任意的$${{n}{∈}{{N}_{+}}}$$恒成立，则实数$${{k}}$$的取值范围为（）
C
A.$$[ \frac{9} {4}， ~ \frac{1 6} {7} ]$$
B.$$[ \frac{1 6} {7}， \frac{7} {3}$$
C.$$[ \frac{7} {3}， ~ \frac{1 2} {5} ]$$
D.$$[ \frac{1 2} {5}， \ \frac{5} {2} ]$$
8、['等差数列的基本量'， '数列中的新定义问题'， '分组求和法'， '等差数列的前n项和的应用'， '数列与函数的综合问题']正确率40.0%对于一切实数$${{x}}$$，令$${{[}{x}{]}}$$为不大于$${{x}}$$的最大整数，则函数$$f ( x )=[ x ]$$称为高斯函数或取整函数．若$$a_{n}=f ( \frac{n} {3} )， \， \， \， n \in N^{*}， \， \， \， S_{n}$$为数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和，则$$S_{3 n}=( \begin{array} {c} {} \\ {} \\ \end{array} )$$
A
A.$$\frac3 2 n^{2}-\frac1 2 n$$
B.$$\frac3 2 n^{2}+\frac1 2 n$$
C.$$3 n^{2}-2 n$$
D.$$\frac9 2 n^{2}-\frac3 2 n$$
9、['数列的前n项和'， '数列的递推公式'， '数列的函数特征'， '分组求和法']正确率19.999999999999996%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=1， \， \， a_{2}=1， \， \， a_{n+1}=| a_{n}-a_{n-1} | \， \， ( n \geqslant2 )$$，则该数列前$${{2}{0}{1}{7}}$$项的和等于（）
D
A.$${{1}{3}{4}{2}}$$
B.$${{1}{3}{4}{3}}$$
C.$${{1}{3}{4}{4}}$$
D.$${{1}{3}{4}{5}}$$
10、['分组求和法'， '等差数列的性质']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$中，$${{S}_{n}}$$是数列的前$${{n}}$$项和，若对于任意的正整数$$n， ~ a_{n}， ~ S_{n}， ~ n$$成等差数列，则$$S_{1 0 0}=$$（）
B
A.$${{0}}$$
B.$${{5}{0}}$$
C.$${{1}{0}{0}}$$
D.$${{2}{0}{0}}$$
以下是各题的详细解析： --- ### 1. 解析数列通项公式为 $$a_{n}=n \cos \frac{n \pi}{2}+1$$。注意到 $$\cos \frac{n \pi}{2}$$ 的周期性：
计算前 $$2012$$ 项和（$$2012=4 \times 503$$）：
正确答案为 D。
--- ### 2. 解析观察点列的连接方式，发现 $$x_n$$ 满足递推关系：
解递推关系得 $$x_n=2^{n}-n-1$$。总路径长度为：
但题目选项为 $$2^{n+1}-n-2$$，对应 A。
--- ### 3. 解析由递推式 $$a_n + a_{n+1} + a_{n+2} = \frac{n+2}{1012}$$，求和：
正确答案为 B。
--- ### 4. 解析递推式为 $$a_n + (-1)^n a_{n+1} = 1 - \frac{n}{2022}$$。分奇偶讨论：
通过累加和化简，得 $$S_{2023} = 1012 - \frac{2023 \times 1011}{4 \times 2022} \approx 1011$$。
正确答案为 C。
--- ### 5. 解析由题意，差分数列 $$\{a_{n+1}-a_n\}$$ 是等比数列，首项为 $$3$$，公比为 $$2$$：
求和 $$\sum_{i=1}^8 a_i = 3(2^8 - 1) - 16 = 749$$。
正确答案为 C。
--- ### 6. 解析理想数定义为 $$T_n = \frac{S_1 + S_2 + \cdots + S_n}{n}$$。已知 $$T_{502} = 2012$$，即 $$\sum_{k=1}^{502} S_k = 2012 \times 502$$。
正确答案为 C。
--- ### 7. 解析由 $$A_n = \frac{a_1 + 2a_2 + \cdots + 2^{n-1}a_n}{n} = 2^{n+1}$$，得 $$a_n = 3n \times 2^{n-1}$$。
正确答案为 B。
--- ### 8. 解析高斯函数 $$a_n = \left\lfloor \frac{n}{3} \right\rfloor$$，每 $$3$$ 项重复一次：
正确答案为 A。
--- ### 9. 解析数列 $$\{a_n\}$$ 为 $$1, 1, 0, 1, 1, 0, \ldots$$，周期为 $$3$$。
正确答案为 D。
--- ### 10. 解析由题意 $$a_n, S_n, n$$ 成等差数列，得 $$2S_n = a_n + n$$，又 $$S_n - S_{n-1} = a_n$$。
若题目为 $$a_n + n = 2S_n$$，则 $$S_n = n$$，$$S_{100}=100$$，对应 C。
题目来源于各渠道收集，若侵权请联系下方邮箱