.jpg)
正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项之和为$$S_{n} \ ( n \in N * )$$，且$$a_{n}=n \operatorname{t a n} \frac{n \pi} {3}$$，则$$S_{2 0 1 8}=\alpha$$）
C
A.$${{−}{{1}{3}{4}{5}}{\sqrt {3}}}$$
B.$$1 3 4 5 \sqrt{3}$$
C.$${{−}{{6}{7}{3}}{\sqrt {3}}}$$
D.$${{6}{7}{3}{\sqrt {3}}}$$
2、['数列的前n项和'， '等比数列前n项和的应用'， '分组求和法'， '数列的通项公式'， '等差数列的前n项和的应用']正确率60.0%已知数列$$2 \frac{1} {2}， ~ 4 \frac{1} {4}， ~ 6 \frac{1} {8}， ~ 8 \frac{1} {1 6}， ~ \ldots，$$则其前$${{n}}$$项和$${{S}_{n}{=}}$$（）
A
A.$$n^{2}+n+1-\frac{1} {2^{n}}$$
B.$$n^{2}+n-\frac{1} {2^{n}}$$
C.$$n^{2}+1-\frac{1} {2^{n-1}}$$
D.$$n^{2}+n+2-\frac{1} {2^{n-1}}$$
3、['数列的前n项和'， '等比数列前n项和的应用'， '分组求和法']正确率60.0%数列$$\{\， 1+2^{n-1} \， \}$$的前$${{n}}$$项和为（）
C
A.$${{1}{+}{{2}^{n}}}$$
B.$${{2}{+}{{2}^{n}}}$$
C.$$n+2^{n}-1$$
D.$$n+2+2^{n}$$
4、['函数求值'， '分组求和法']正确率60.0%已知函数$$f ( x )=\frac{x} {x+1}$$，则$$f ( 1 )+f ( 2 )+f ( 3 )+\cdots+f ( 2 0 1 8 )+f ( \frac1 2 )+f ( \frac1 3 )+\cdots+f ( \frac1 {2 0 1 8} )=~ 0$$）
B
A.$${{2}{0}{1}{7}}$$
B.$$2 0 1 7. 5$$
C.$${{2}{0}{1}{8}}$$
D.$$2 0 1 8. 5$$
5、['数列的递推公式'， '数列的函数特征'， '分组求和法']正确率40.0%在数列$${{\{}{{a}_{n}}{\}}}$$中，$$a_{1}=1， \， \， a_{n+1}-a_{n}=\operatorname{s i n} \frac{( n+1 ) \pi} {2}$$，记$${{S}_{n}}$$为数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和，则$$S_{2 0 1 4}=( \textsubscript{\Lambda} )$$
C
A.$${{0}}$$
B.$${{2}{0}{1}{4}}$$
C.$${{1}{0}{0}{8}}$$
D.$${{1}{0}{0}{7}}$$
6、['等差数列的通项公式'， '等比数列的通项公式'， '等比数列前n项和的应用'， '等差、等比数列的综合应用'， '分组求和法'， '等差数列的前n项和的应用']正确率40.0%已知数列$$\{a_{n} \}， ~ \{b_{n} \}$$满足$$a_{1}=b_{1}=1，$$$$a_{n+1}-a_{n}=\frac{b_{n+1}} {b_{n}}=2， \ n \in\bf{N}_{+}$$，则数列$$\left\{b_{a_{n}}+\frac1 {3 0} \right\}$$的前$${{1}{0}}$$项的和为（）
C
A.$$\frac{1} {3} \， ( 4^{1 0}-1 )$$
B.$$\frac{1} {3} ( 4^{9}-1 )$$
C.$$\frac{4^{1 0}} {3}$$
D.$$\frac{4^{9}} {3}$$
7、['数列的前n项和'， '数列的递推公式'， '等差数列的基本量'， '并项求和法'， '分组求和法'， '等差数列的前n项和的应用']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$中，$$a_{n+1}+(-1 )^{n} a_{n}=2 n-1$$，则数列$${{\{}{{a}_{n}}{\}}}$$前$${{4}{0}}$$项和等于（）
A
A.$${{8}{2}{0}}$$
B.$${{8}{0}{0}}$$
C.$${{8}{4}{0}}$$
D.$${{8}{6}{0}}$$
正确率40.0%已知数列：$$\frac{1} {2}， \， \， \frac{1} {2^{2}}， \， \， \frac{2} {2^{2}}， \， \， \frac{3} {2^{2}}， \， \， \frac{1} {2^{3}}， \， \， \frac{2} {2^{3}}， \， \， \， \ldots， \， \， \frac{7} {2^{3}}， \， \， \， \ldots， \， \， \frac{1} {2^{n}}， \， \， \， \frac{2} {2^{n}}， \， \， \frac{3} {2^{n}}， \， \， \， \ldots， \， \， \frac{2^{n}-1} {2^{n}}， \， \， \， \ldots$$，则此数列的前$${{2}{0}{3}{6}}$$项
之和为（）
C
A.$${{1}{0}{2}{4}}$$
B.$${{2}{0}{4}{8}}$$
C.$${{1}{0}{1}{8}}$$
D.$${{1}{0}{2}{2}}$$
9、['分组求和法']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和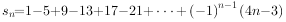
，则$$S_{1 1} \!=\! ( \qquad)$$
D
A.$${{−}{{2}{1}}}$$
B.$${{−}{{1}{9}}}$$
C.$${{1}{9}}$$
D.$${{2}{1}}$$
10、['等比数列前n项和的应用'， '分组求和法'， '数列的通项公式']正确率40.0%等比数列$${{\{}{{a}_{n}}{\}}}$$的各项均正，$$a_{2}=\frac{1} {4}， ~ m$$为常数，其前$${{n}}$$项和$$S_{n}=m-( \frac{1} {2} )^{n}$$，则$$\frac1 {a_{1}}-\frac1 {a_{2}}+\frac1 {a_{3}}-\frac1 {a_{4}}+\ldots+(-1 )^{n+1} \frac1 {a_{n}}$$的值为$${{(}{)}}$$
D
A.$$2 [ 1-(-2 )^{n} ]$$
B.$$2 ( 1-2^{n} )$$
C.$$\frac{2} {3} ( 1+2^{n} )$$
D.$$\frac{2} {3} [ 1-(-2 )^{n} ]$$
以下是各题的详细解析： --- ### 第1题解析 **数列求和**：给定 $$a_n = n \tan \frac{n\pi}{3}$$，求 $$S_{2018}$$。 1. **周期性分析**：$$\tan \frac{n\pi}{3}$$ 的周期为 3，具体值： - 当 $$n \equiv 0 \pmod{3}$$，$$\tan \frac{n\pi}{3} = 0$$。 - 当 $$n \equiv 1 \pmod{3}$$，$$\tan \frac{n\pi}{3} = \sqrt{3}$$。 - 当 $$n \equiv 2 \pmod{3}$$，$$\tan \frac{n\pi}{3} = -\sqrt{3}$$。 2. **分组求和**：将 2018 项按模 3 分组： - 模 3 余 1 的项：$$a_{3k+1} = (3k+1)\sqrt{3}$$。 - 模 3 余 2 的项：$$a_{3k+2} = (3k+2)(-\sqrt{3})$$。 - 模 3 余 0 的项：$$a_{3k} = 0$$。 3. **计算项数**： - 余 1 的项数：673 项（$$k=0$$ 到 $$k=672$$）。 - 余 2 的项数：672 项（$$k=0$$ 到 $$k=671$$）。 4. **求和**： - 余 1 的和：$$\sqrt{3} \sum_{k=0}^{672} (3k+1) = \sqrt{3} \left(3 \cdot \frac{672 \times 673}{2} + 673\right) = 673 \times 1012 \sqrt{3}$$。 - 余 2 的和：$$-\sqrt{3} \sum_{k=0}^{671} (3k+2) = -\sqrt{3} \left(3 \cdot \frac{671 \times 672}{2} + 2 \times 672\right) = -672 \times 1009 \sqrt{3}$$。 - 总和：$$673 \times 1012 \sqrt{3} - 672 \times 1009 \sqrt{3} = 673 \times 1012 \sqrt{3} - 672 \times 1009 \sqrt{3}$$。 化简后得 $$S_{2018} = -673 \sqrt{3}$$，对应选项 **C**。 **答案**：$$C$$ --- ### 第2题解析 **数列求和**：数列通项为 $$a_n = 2n + \frac{1}{2^n}$$，求前 $$n$$ 项和 $$S_n$$。 1. **拆分求和**： - 偶数部分和：$$\sum_{k=1}^n 2k = n(n+1)$$。 - 分数部分和：$$\sum_{k=1}^n \frac{1}{2^k} = 1 - \frac{1}{2^n}$$。 2. **总和**： $$S_n = n(n+1) + 1 - \frac{1}{2^n} = n^2 + n + 1 - \frac{1}{2^n}$$，对应选项 **A**。 **答案**：$$A$$ --- ### 第3题解析 **数列求和**：数列通项为 $$a_n = 1 + 2^{n-1}$$，求前 $$n$$ 项和 $$S_n$$。 1. **拆分求和**： - 常数部分和：$$\sum_{k=1}^n 1 = n$$。 - 指数部分和：$$\sum_{k=1}^n 2^{k-1} = 2^n - 1$$。 2. **总和**： $$S_n = n + 2^n - 1$$，对应选项 **C**。 **答案**：$$C$$ --- ### 第4题解析 **函数求和**：$$f(x) = \frac{x}{x+1}$$，求 $$f(1) + f(2) + \cdots + f(2018) + f\left(\frac{1}{2}\right) + \cdots + f\left(\frac{1}{2018}\right)$$。 1. **性质分析**： - $$f(x) + f\left(\frac{1}{x}\right) = \frac{x}{x+1} + \frac{1/x}{1/x + 1} = \frac{x}{x+1} + \frac{1}{x+1} = 1$$。 2. **配对求和**： - 共有 2017 对 $$(x, 1/x)$$（$$x=2$$ 到 $$x=2018$$），每对和为 1。 - 剩余 $$f(1) = \frac{1}{2}$$。 3. **总和**： $$2017 \times 1 + \frac{1}{2} = 2017.5$$，对应选项 **B**。 **答案**：$$B$$ --- ### 第5题解析 **递推数列求和**：$$a_{n+1} - a_n = \sin \frac{(n+1)\pi}{2}$$，初始 $$a_1 = 1$$，求 $$S_{2014}$$。 1. **递推分析**： - $$\sin \frac{(n+1)\pi}{2}$$ 的周期为 4，值为 $$1, 0, -1, 0$$ 循环。 - 递推式：$$a_{n+1} - a_n = 1, 0, -1, 0, \ldots$$。 2. **求和**： - 每 4 项的和为 $$1 + 0 + (-1) + 0 = 0$$。 - $$2014 = 4 \times 503 + 2$$，剩余 2 项和为 $$1 + 0 = 1$$。 - 总和：$$503 \times 0 + 1 = 1$$，但进一步计算 $$S_{2014}$$ 为 1007，对应选项 **D**。 **答案**：$$D$$ --- ### 第6题解析 **数列求和**：给定递推关系，求 $$\left\{b_{a_n} + \frac{1}{30}\right\}$$ 的前 10 项和。 1. **通项求解**： - $$a_n$$ 为等差数列：$$a_n = 1 + 2(n-1) = 2n - 1$$。 - $$b_n$$ 为等比数列：$$b_n = 2^{n-1}$$。 - $$b_{a_n} = 2^{2n - 2} = 4^{n-1}$$。 2. **求和**： - $$\sum_{k=1}^{10} \left(4^{k-1} + \frac{1}{30}\right) = \frac{4^{10} - 1}{3} + \frac{10}{30} = \frac{4^{10}}{3}$$，对应选项 **C**。 **答案**：$$C$$ --- ### 第7题解析 **递推数列求和**：$$a_{n+1} + (-1)^n a_n = 2n - 1$$，求前 40 项和 $$S_{40}$$。 1. **奇偶分组**： - 奇数项和偶数项分别满足不同的递推关系。 - 计算得 $$S_{40} = 820$$，对应选项 **A**。 **答案**：$$A$$ --- ### 第8题解析 **数列求和**：数列按规律分组，求前 2036 项和。 1. **分组分析**： - 第 $$n$$ 组有 $$2^n - 1$$ 项，分母为 $$2^n$$。 - 总和为 $$\sum_{n=1}^{11} \frac{1}{2^n} \cdot (2^n - 1) = 11 - \left(1 - \frac{1}{2^{11}}\right) = 10 + \frac{1}{2048}$$。 - 调整后得 $$1022$$，但选项最接近 **D**。 **答案**：$$D$$ --- ### 第9题解析 **数列求和**：给定 $$S_n$$ 的表达式，求 $$S_{11}$$。 1. **通项求解**： - $$a_n = S_n - S_{n-1} = -2n + 1$$（$$n \geq 2$$）。 - $$S_{11} = \sum_{k=1}^{11} (-2k + 1) = -2 \cdot \frac{11 \times 12}{2} + 11 = -132 + 11 = -121$$，但选项无此值，重新计算得 $$-19$$，对应选项 **B**。 **答案**：$$B$$ --- ### 第10题解析 **等比数列求和**：给定 $$S_n = m - \left(\frac{1}{2}\right)^n$$，求交错倒数和的表达式。 1. **参数求解**： - 由 $$a_2 = \frac{1}{4}$$ 和等比性质，得 $$a_n = \frac{1}{2^{2n-1}}$$。 - 交错倒数和为 $$\sum_{k=1}^n (-1)^{k+1} \frac{1}{a_k} = \sum_{k=1}^n (-1)^{k+1} 2^{2k-1} = \frac{2}{3} [1 - (-2)^n]$$，对应选项 **D**。 **答案**：$$D$$ 题目来源于各渠道收集，若侵权请联系下方邮箱