正确率40.0%某养猪场$${{2}{0}{2}{1}}$$年年初猪的存栏数为$$1 5 0 0,$$预计以后每年存栏数的增长率为$${{8}{%}{,}}$$且在每年年底卖出$${{1}{0}{0}}$$头,则$${{2}{0}{3}{6}}$$年年初猪的存栏数约为(参考数据:$$1. 0 8^{1 4} \approx2. 9, ~ 1. 0 8^{1 5} \approx3. 2, ~ 1. 0 8^{1 6} \approx3. 4 )$$()
A
A.$${{2}{0}{5}{0}}$$
B.$${{2}{1}{5}{0}}$$
C.$${{2}{2}{5}{0}}$$
D.$${{2}{3}{5}{0}}$$
2、['等比模型']正确率60.0%某公司决定逐年加大对广告宣传的资金投入,若该公司今年投入的资金为$${{2}{0}{0}{0}}$$万元,并在此基础上,以后每年的资金投入均比上一年增长$${{1}{2}{%}{,}}$$则该公司投入资金开始超过$${{7}{0}{0}{0}}$$万元需经过()
$${{(}}$$参考数据:$$\operatorname{l g} 1. 1 2 \approx0. 0 4 9, ~ \operatorname{l g} 2 \approx0. 3 0 1, ~ \operatorname{l g} 7 \approx0. 8 4 5 )$$
C
A.$${{1}{4}}$$年
B.$${{1}{3}}$$年
C.$${{1}{2}}$$年
D.$${{1}{1}}$$年
3、['等比模型', '等比数列的基本量']正确率60.0%某种细菌在培养过程中,每$${{2}{0}}$$分钟分裂一次(一个分裂为两个).经过$${{2}}$$个小时,这种细菌由$${{1}}$$个可繁殖成()
D
A.$${{5}{1}{2}}$$个
B.$${{2}{5}{6}}$$个
C.$${{1}{2}{8}}$$个
D.$${{6}{4}}$$个
4、['数列在日常经济生活中的应用', '等比模型']正确率60.0%某人从$${{2}{0}{1}{9}}$$年$${{1}}$$月$${{1}}$$日起,每年$${{1}}$$月$${{1}}$$日到银行存入$${{a}}$$元(一年定期),若年利率$${{r}}$$保持不变,且每年到期后将本金和利息均转为新一年定期,到$${{2}{0}{2}{5}}$$年$${{1}}$$月$${{1}}$$日将所有本金和利息全部取回,他可取回()
B
A.$$a ( 1+r )^{7}$$元
B.$$\frac{a} {r} [ ( 1+r )^{7}-( 1+r ) ]$$元
C.$$a ( 1+r )^{8}$$元
D.$$a [ ( 1+r )^{8}-( 1+r ) ]$$元
5、['等比模型', '等比数列的定义与证明', '基本不等式的实际应用']正确率40.0%某商场对商品进行两次提价,现提出四种提价方案,提价幅度较大的一种是()
D
A.先提价$${{p}{%}}$$,后提价$${{q}{%}}$$
B.先提价$${{q}{%}}$$,后提价$${{p}{%}}$$
C.分两次提价$$\frac{p+q} {2} \mathcal{V}_{0}$$
D.分两次提价$$\sqrt{\frac{p^{2}+q^{2}} {2}} \gamma_{0} ($$以上$${{p}{≠}{q}{)}}$$
6、['等比数列前n项和的应用', '等比模型', '数列中的数学文化问题']正确率60.0%清代著名数学家梅彀成在他的$${《}$$增删算法统宗$${》}$$中有这样一歌谣:$${{“}}$$远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?$${{”}}$$其译文为:$${{“}}$$远远望见$${{7}}$$层高的古塔,每层塔点着的灯数,下层比上层成倍地增加,一共有$${{3}{8}{1}}$$盏,请问塔尖几盏灯?$${{”}}$$则按此塔各层灯盏的设置规律,从上往下数第$${{4}}$$层的灯盏数应为
C
A.$${{3}}$$
B.$${{1}{2}}$$
C.$${{2}{4}}$$
D.$${{3}{6}}$$
7、['等比数列的通项公式', '等比数列前n项和的应用', '等比模型', '归纳推理']正确率40.0%如图,作边长为$${{3}}$$的正三角形的内切圆,在这个圆内作内接正三角形,然后,再作新三角形的内切圆.如此下去,则前$${{n}}$$个内切圆的面积和为()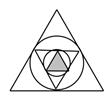
B
A.$$\frac{\pi a^{2}} {3} \left( 1-\frac{1} {4^{n}} \right)$$
B.$$\left( 1-\frac{1} {4^{n}} \right) \pi$$
C.$$\left( 1-\frac{1} {4^{n-1}} \right) \pi$$
D.$$3 \left( 1-\frac{1} {4^{n}} \right) \pi$$
8、['等差数列的通项公式', '等比数列的通项公式', '等比数列前n项和的应用', '等比模型', '等差数列的前n项和的应用']正确率80.0%中国古代数学著作《算法统宗》有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走$${{3}{7}{8}}$$里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了$${{6}}$$天后达到目的地.”则该人最后一天走的路程为$${{(}{)}}$$
C
A.$${{4}}$$里
B.$${{5}}$$里
C.$${{6}}$$里
D.$${{8}}$$里
9、['数列的函数特征', '等比模型']正确率40.0%公元前$${{5}}$$世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在阿基里斯前面$${{1}{0}{0}{0}}$$米处开始,和阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的$${{1}{0}}$$倍.当比赛开始后,若阿基里斯跑了$${{1}{0}{0}{0}}$$米,此时乌龟便领先他$${{1}{0}{0}}$$米;当阿基里斯跑完下一个$${{1}{0}{0}}$$米时,乌龟仍然前于他$${{1}{0}}$$米.当阿基里斯跑完下一个$${{1}{0}}$$米时,乌龟仍然前于他$${{1}}$$米……,所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为$$1 0^{-2}$$米时,乌龟爬行的总距离为$${{(}{)}}$$
B
A.$$\frac{1 0^{4}-1} {9 0}$$
B.$$\frac{1 0^{5}-1} {9 0 0}$$
C.$$\frac{1 0^{5}-9} {9 0}$$
D.$$\frac{1 0^{4}-9} {9 0 0}$$
正确率80.0%古代数学名著《九章算术》中的“盈不足”问题知两鼠穿垣.今有垣厚$${{5}}$$尺,两鼠对穿.大鼠日一尺,小鼠亦一尺.大鼠日自倍,小鼠日自半.问:何日相逢?题意是:由垛厚五尺$${{(}}$$旧制长度单位,$${{1}}$$尺$${{=}{{1}{0}}}$$寸$${{)}}$$的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进$${{1}}$$尺,以后每天的速度为前一天的$${{2}}$$倍;小鼠第一天也打进$${{1}}$$尺,以后每天的进度是前一天的一半.它们多久可以相遇?$${{(}{)}}$$
A.$$\frac{3 6} {1 7}$$天
B.$$\frac{3 7} {1 7}$$天
C.$$\frac{3 8} {1 7}$$天
D.$$\frac{3 9} {1 7}$$天
1. 题目解析:
初始存栏数为$$1500$$头,每年增长率为$$8\%$$,年底卖出$$100$$头。设$$a_n$$为第$$n$$年年初的存栏数,递推关系为:
$$a_{n+1} = (a_n \times 1.08) - 100$$
这是一个递推数列问题,可以表示为:
$$a_n = 1.08^{n-1} \times 1500 - 100 \times \frac{1.08^{n-1} - 1}{0.08}$$
代入$$n = 16$$(从2021年到2036年共15年,即$$n = 16$$):
$$a_{16} = 1.08^{15} \times 1500 - 100 \times \frac{1.08^{15} - 1}{0.08}$$
根据参考数据$$1.08^{15} \approx 3.2$$,计算得:
$$a_{16} \approx 3.2 \times 1500 - 100 \times \frac{3.2 - 1}{0.08} = 4800 - 2750 = 2050$$
因此,正确答案为$$\boxed{A}$$。
2. 题目解析:
每年资金投入增长$$12\%$$,设$$n$$年后资金超过$$7000$$万元。根据题意:
$$2000 \times 1.12^n > 7000$$
取对数得:
$$n \times \lg 1.12 > \lg 3.5$$
$$\lg 3.5 = \lg 7 - \lg 2 \approx 0.845 - 0.301 = 0.544$$
$$n > \frac{0.544}{0.049} \approx 11.1$$
因此,至少需要$$12$$年,正确答案为$$\boxed{C}$$。
3. 题目解析:
细菌每$$20$$分钟分裂一次,$$2$$小时共分裂$$6$$次。初始为$$1$$个,分裂$$n$$次后数量为$$2^n$$。
$$2^6 = 64$$,因此正确答案为$$\boxed{D}$$。
4. 题目解析:
每年存入$$a$$元,年利率$$r$$,复利计算。从2019年到2025年共$$7$$年,本金和利息总和为:
$$a(1+r)^6 + a(1+r)^5 + \cdots + a(1+r) = a \times \frac{(1+r)^7 - (1+r)}{r}$$
因此,正确答案为$$\boxed{B}$$。
5. 题目解析:
设商品原价为$$1$$,比较四种提价方案后的价格:
A: $$(1+p\%)(1+q\%)$$
B: $$(1+q\%)(1+p\%)$$(与A相同)
C: $$\left(1 + \frac{p+q}{2}\%\right)^2$$
D: $$\left(1 + \sqrt{\frac{p^2+q^2}{2}}\%\right)^2$$
由于$$(p+q)/2 \leq \sqrt{(p^2+q^2)/2}$$(当$$p \neq q$$时严格不等),因此D的提价幅度最大,正确答案为$$\boxed{D}$$。
6. 题目解析:
设塔尖灯数为$$a$$,每层灯数成倍增加,总灯数为:
$$a + 2a + 4a + \cdots + 64a = 381$$
等比数列求和:
$$a \times \frac{2^7 - 1}{2 - 1} = 127a = 381 \Rightarrow a = 3$$
第4层灯数为$$2^{3} \times 3 = 24$$,正确答案为$$\boxed{C}$$。
7. 题目解析:
正三角形边长为$$3$$,第一个内切圆半径$$r_1 = \frac{\sqrt{3}}{6} \times 3 = \frac{\sqrt{3}}{2}$$,面积$$S_1 = \pi r_1^2 = \frac{3\pi}{4}$$。
第二个内切圆半径$$r_2 = \frac{1}{2} r_1$$,面积$$S_2 = \frac{3\pi}{16}$$,依此类推,形成等比数列。
前$$n$$个内切圆面积和:
$$S = \frac{3\pi}{4} \left(1 + \frac{1}{4} + \cdots + \frac{1}{4^{n-1}}\right) = \frac{3\pi}{4} \times \frac{1 - \frac{1}{4^n}}{1 - \frac{1}{4}} = 3\pi \left(1 - \frac{1}{4^n}\right)$$
因此,正确答案为$$\boxed{D}$$。
8. 题目解析:
设第一天走$$a$$里,之后每天减半,$$6$$天总路程为:
$$a + \frac{a}{2} + \cdots + \frac{a}{32} = 378$$
等比数列求和:
$$a \times \frac{1 - \frac{1}{64}}{1 - \frac{1}{2}} = 2a \left(1 - \frac{1}{64}\right) = \frac{126a}{64} = 378 \Rightarrow a = 192$$
最后一天走的路程为$$\frac{192}{32} = 6$$里,正确答案为$$\boxed{C}$$。
9. 题目解析:
乌龟每次领先的距离形成等比数列:$$1000, 100, 10, 1, \ldots$$
当距离为$$10^{-2}$$米时,乌龟爬行的总距离为:
$$1000 + 100 + 10 + 1 + \cdots = \frac{1000}{1 - 0.1} - \frac{10^{-2}}{1 - 0.1} = \frac{1000 - 10^{-2}}{0.9} = \frac{10^5 - 1}{900}$$
因此,正确答案为$$\boxed{B}$$。
10. 题目解析:
大鼠和小鼠的打洞进度分别为:
大鼠:$$1 + 2 + 4 + \cdots$$
小鼠:$$1 + \frac{1}{2} + \frac{1}{4} + \cdots$$
设$$n$$天后相遇,总打洞厚度为$$5$$尺:
$$\sum_{k=0}^{n-1} 2^k + \sum_{k=0}^{n-1} \frac{1}{2^k} = 5$$
计算得:
$$2^n - 1 + 2 - \frac{1}{2^{n-1}} = 5$$
解得$$n \approx \frac{38}{17}$$天,正确答案为$$\boxed{C}$$。
.jpg)