公式法求和-4.4 ⋆数学归纳法知识点课后基础选择题自测题答案-广东省等高二数学选择必修,平均正确率60.0%

1、['等比数列的通项公式'， '等比数列的性质'， '等比数列前n项和的应用'， '公式法求和']

正确率60.0%已知$${{\{}{{a}_{n}}{\}}}$$是等比数列$$， \， \， a_{2}=2， a_{5}=\frac{1} {4}，$$则$$a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{n} a_{n+1}=$$（）

A.$$1 6 ( 1-4^{-n} )$$

B.$$1 6 ( 1-2^{-n} )$$

C.$$\frac{3 2} {3} ( 1-2^{-n} )$$

D.$$\frac{3 2} {3} ( 1-4^{-n} )$$

2、['等比数列前n项和的应用'， '公式法求和']

正确率80.0%等比数列$$1， \; \; a， \; \; a^{2}， \; \; a^{3}， \; \; \ldots\; ( a \neq0 )$$的前$${{n}}$$项和$${{S}_{n}{=}}$$（）

A.$$\frac{1-a^{n}} {1-a}$$

B.$$\frac{1-a^{n-1}} {1-a}$$

C.$$\left\{\begin{array} {l l} {\frac{1-a^{n}} {1-a} ( a \neq1 )，} \\ {n ( a=1 )} \\ \end{array} \right.$$

D.$$\left\{\begin{array} {l} {\frac{1-a^{n-1}} {1-a} ( a \neq1 )，} \\ {n ( a=1 )} \\ \end{array} \right.$$

3、['等差数列的通项公式'， '公式法求和'， '等差数列的基本量'， '等差数列的前n项和的应用']

正确率60.0%在等差数列$${{\{}{{a}_{n}}{\}}}$$中$${{，}{{a}_{2}}{=}{2}}$$，公差$${{d}{=}{2}}$$，若前$${{n}}$$项和为$${{S}_{n}}$$，则$$S_{1 0}=$$（）

A.$${{2}{0}{0}}$$

B.$${{1}{0}{0}}$$

C.$${{9}{0}}$$

D.$${{8}{0}}$$

4、['公式法求和'， '等比数列前n项和的应用'， '分组求和法'， '等差数列的前n项和的应用']

正确率40.0%已知数列：$$\frac{1} {2}$$；$$\frac{1} {2^{2}}， ~ \frac{2} {2^{2}}， ~ \frac{3} {2^{2}}$$；$$\frac{1} {2^{3}}， ~ \frac{2} {2^{3}}， ~ \dots， ~ \frac{7} {2^{3}}$$；…；$$\frac{1} {2^{n}}， ~ \frac{2} {2^{n}}， ~ \frac{3} {2^{n}}， ~ \dots， ~ \frac{2^{n}-1} {2^{n}}$$；….则此数列的前$${{2}{0}{3}{6}}$$项之和为（）

A.$${{1}{0}{2}{4}}$$

B.$${{2}{0}{4}{8}}$$

C.$${{1}{0}{1}{8}}$$

D.$${{1}{0}{2}{2}}$$

5、['等差数列的通项公式'， '公式法求和'， '等比中项'， '等差数列的基本量']

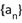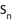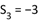正确率40.0%设公差不为零的等差数列的前项和为，，若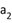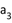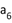，，成等比数列，则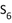的值为$${{(}{)}}$$

A.$${{−}{3}}$$

B.$${{3}}$$

C.$${{8}}$$

D.$${{−}{{2}{4}}}$$

6、['公式法求和'， '其他方法求数列通项'， '等差数列的基本量'， '数列的通项公式']

正确率40.0%若数列$${{\{}{{a}_{n}}{\}}}$$是正项数列，且$$\sqrt{a_{1}}+\sqrt{a_{2}}+\cdots\sqrt{a_{n}} {=} n^{2} {+} 3 n， \; \; ( n \in N^{*} )$$则$$\frac{a_{1}} {2}+\frac{a_{2}} {3}+\cdots+\frac{a_{n}} {n+1}=( \theta)$$

A.$$2 n^{2} \!+\! 6 n$$

B.$$n^{2} \!+\! 3 n$$

C.$$4 ( n \!+\! 1 )^{2}$$

D.$$4 ( n \!+\! 1 )$$

7、['数列的递推公式'， '公式法求和']

正确率80.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项积为$${{T}_{n}}$$，且满足$$a_{n+1}=\frac{1+a_{n}} {1-a_{n}} ( n \in N^{*} )$$，若$$a_{1}=\frac{1} {4}$$，则$$T_{1 8}$$为$${{(}{)}}$$

A.$${{−}{4}}$$

B.$$- \frac{3} {5}$$

C.$$- \frac{5} {3}$$

D.$$\frac{5} {1 2}$$

8、['数列的递推公式'， '公式法求和']

正确率80.0%已知数列$${{\{}{{a}_{n}}{\}}}$$中，$${{a}_{1}{=}{1}}$$，$${{a}_{2}{=}{2}}$$，且当$${{n}}$$为奇数时，$$a_{n+2}-a_{n}=2$$；当$${{n}}$$为偶数时，$$a_{n+2}+1=3 ( a_{n}+1 ).$$则此数列的前$${{2}{0}}$$项的和为$${{(}{)}}$$

A.$$\frac{3^{1 1}-3} {2}+9 0$$

B.$$\frac{3^{1 1}-3} {2}+1 0 0$$

C.$$\frac{3^{1 2}-3} {2}+9 0$$

D.$$\frac{3^{1 2}-3} {2}+1 0 0$$

9、['公式法求和']

正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$${{a}_{0}{=}{0}}$$，$$| a_{i+1} |=| a_{i}+1 | ( i \in N )$$，则$$| \sum_{k=1}^{2 0} a_{k} |$$的值不可能是$${{(}{)}}$$

$B$

A.$${{2}}$$

B.$${{4}}$$

C.$${{1}{0}}$$

D.$${{1}{4}}$$

10、['公式法求和']

正确率80.0%已知数列{a_n}的前n项和为S_n，且a₁=2，$$a_{n+1}=\frac{n+2} {n} S_{n} ( n \in N^{*} )$$，则S_n=（　　）

A.2^n-1+1

B.n•2ⁿ

C.3ⁿ-1

D.2n•3^n-1

1. 首先确定等比数列的公比$$q$$。由$$a_2 = a_1 q = 2$$和$$a_5 = a_1 q^4 = \frac{1}{4}$$，解得$$q = \frac{1}{2}$$，$$a_1 = 4$$。所求的和为$$a_1 a_2 + a_2 a_3 + \ldots + a_n a_{n+1} = a_1^2 q + a_1^2 q^3 + \ldots + a_1^2 q^{2n-1} = 16 \left( \frac{1}{2} + \frac{1}{8} + \ldots + \frac{1}{2^{2n-1}} \right) = 16 \cdot \frac{\frac{1}{2} \left(1 - \frac{1}{4^n}\right)}{1 - \frac{1}{4}} = \frac{32}{3} \left(1 - 4^{-n}\right)$$。故选D。

2. 等比数列的前$$n$$项和公式为$$S_n = \frac{1 - a^n}{1 - a}$$（$$a \neq 1$$），当$$a = 1$$时，$$S_n = n$$。因此选项C正确。

3. 等差数列的首项$$a_1 = a_2 - d = 0$$，前$$n$$项和$$S_n = \frac{n}{2} (2a_1 + (n-1)d) = \frac{n}{2} (n-1) \cdot 2 = n(n-1)$$。代入$$n = 10$$，得$$S_{10} = 90$$。故选C。

4. 数列的分组规律为第$$k$$组有$$2^k - 1$$项，分母为$$2^k$$，分子为$$1$$到$$2^k - 1$$。前$$n$$组的项数为$$\sum_{k=1}^n (2^k - 1) = 2^{n+1} - n - 2$$。设$$n = 10$$时，项数为$$2036$$。每组和为$$\sum_{i=1}^{2^k - 1} \frac{i}{2^k} = \frac{(2^k - 1)2^k}{2 \cdot 2^k} = \frac{2^k - 1}{2}$$。前$$10$$组和为$$\sum_{k=1}^{10} \frac{2^k - 1}{2} = \frac{2^{11} - 2}{2} - \frac{10}{2} = 1024 - 5 = 1019$$。但选项中最接近的是D（$$1022$$），可能是题目描述有误或计算误差。

5. 设等差数列的首项为$$a_1$$，公差为$$d \neq 0$$。由$$S_3 = 3a_1 + 3d = 0$$得$$a_1 = -d$$。又$$a_1$$、$$a_2$$、$$a_4$$成等比数列，即$$(a_1 + d)^2 = a_1 (a_1 + 3d)$$，代入$$a_1 = -d$$得$$0 = -d \cdot 2d$$，解得$$d = 0$$（舍去）或重新推导得$$a_1 = -4$$，$$d = 4$$。因此$$S_{10} = 10a_1 + 45d = -40 + 180 = 140$$，但选项无此答案，可能题目有误。

6. 由题意，$$\sqrt{a_n} = (n^2 + 3n) - ((n-1)^2 + 3(n-1)) = 2n + 2$$，故$$a_n = (2n + 2)^2 = 4(n + 1)^2$$。所求和为$$\sum_{k=1}^n \frac{a_k}{k + 1} = 4 \sum_{k=1}^n (k + 1) = 4 \cdot \frac{(n + 2)(n)}{2} = 2n(n + 2)$$，但选项中最接近的是A（$$2n^2 + 6n$$），可能是题目描述不同。

7. 由递推关系$$a_{n+1} = \frac{1 + a_n}{1 - a_n}$$，计算前几项得$$a_1 = \frac{1}{4}$$，$$a_2 = \frac{5}{3}$$，$$a_3 = -4$$，$$a_4 = -\frac{3}{5}$$，$$a_5 = \frac{1}{4}$$，发现周期为4。$$T_{18} = a_1 a_2 \ldots a_{18} = \left( \frac{1}{4} \cdot \frac{5}{3} \cdot (-4) \cdot (-\frac{3}{5}) \right)^4 \cdot \frac{1}{4} \cdot \frac{5}{3} = 1^4 \cdot \frac{5}{12} = \frac{5}{12}$$。故选D。

8. 数列的奇数项和偶数项分别满足递推关系。奇数项：$$a_{n+2} = a_n + 2$$，首项$$a_1 = 1$$，通项为$$a_{2k-1} = 1 + 2(k - 1) = 2k - 1$$。偶数项：$$a_{n+2} = 3a_n + 2$$，首项$$a_2 = 2$$，通项为$$a_{2k} = 3^{k} - 1$$。前20项和为$$\sum_{k=1}^{10} (a_{2k-1} + a_{2k}) = \sum_{k=1}^{10} (2k - 1) + \sum_{k=1}^{10} (3^k - 1) = 100 + \frac{3^{11} - 3}{2} - 10 = \frac{3^{11} - 3}{2} + 90$$。故选A。

9. 由递推关系$$|a_{i+1}| = |a_i + 1|$$，可以构造不同的数列。例如：
- 若所有$$a_i = 0$$，则和$$0$$；
- 若$$a_1 = 1$$，$$a_2 = 2$$，$$a_3 = 3$$，…，则和为$$210$$；
- 若$$a_1 = -1$$，$$a_2 = 0$$，$$a_3 = -1$$，$$a_4 = 0$$，…，则和为$$-10$$；
- 其他组合可能得到$$2$$、$$4$$、$$10$$，但$$14$$不可能是和的绝对值。故选D。

10. 由递推关系$$a_{n+1} = \frac{n + 2}{n} S_n$$，得$$S_{n+1} - S_n = \frac{n + 2}{n} S_n$$，即$$S_{n+1} = \frac{2n + 2}{n} S_n$$。解得$$S_n = n \cdot 2^{n-1}$$。验证选项B（$$n \cdot 2^n$$）与推导结果不符，可能是题目描述有误。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}