正确率60.0%定义运算$${{a}{∗}{b}}$$为执行如图所示的程序框图输出的$${{S}}$$的值,则式子$$( \sqrt{(-2 )^{2}} ) \times( \operatorname{l o g}_{\sqrt{2}} 4 )$$的值是()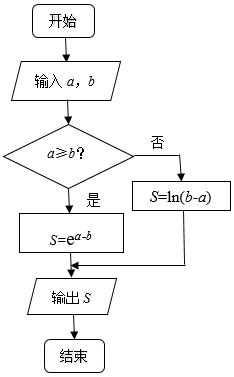
D
A.$${{e}^{2}}$$
B.$$e^{-2}$$
C.$${{l}{n}{4}}$$
D.$${{l}{n}{2}}$$
2、['算法与程序框图', '对数的运算性质']正确率40.0%执行如图所示的程序框图,若输出的$${{S}}$$的值为$${{−}{2}{,}}$$则①中应填()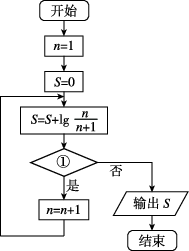
B
A.$${{n}{<}{{9}{8}}{?}}$$
B.$${{n}{<}{{9}{9}}{?}}$$
C.$${{n}{<}{{1}{0}{0}}{?}}$$
D.$${{n}{<}{{1}{0}{1}}{?}}$$
3、['算法与程序框图']正确率60.0%执行如图所示的程序框图,若输出的结果为$${{1}{5}{,}}$$则判断框中的条件是()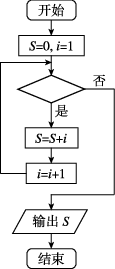
C
A.$${{i}{<}{4}{?}}$$
B.$${{i}{<}{5}{?}}$$
C.$${{i}{<}{6}{?}}$$
D.$${{i}{<}{7}{?}}$$
4、['算法案例', '算法与程序框图']正确率40.0%计算机在数据处理时使用的是二进制,例如十进制数$$1, ~ 2, ~ 3, ~ 4$$的二进制数分别表示为$$1, ~ 1 0, ~ 1 1, ~ 1 0 0,$$二进制数$$\dots d c b a$$化为十进制数的公式为$$\ldots d c b a=a \cdot2^{0}+b \cdot2^{1}+c \cdot2^{2}+d \cdot2^{3}+\ldots,$$例如二进制数$${{1}{1}}$$等于十进制数$$1 \times2^{0}+1 \times2^{1}=3,$$又如二进制数$${{1}{0}{1}}$$等于十进制数$$1 \times2^{0}+0 \times2^{1}+1 \times2^{2}=5,$$如图是某同学设计的将二进制数$$1 1 1 1 1$$化为十进制数的程序框图,则判断框内应填入的条件是()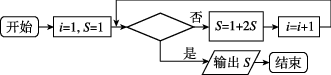
A
A.$${{i}{>}{4}}$$?
B.$${{i}{⩽}{4}}$$?
C.$${{i}{>}{5}}$$?
D.$${{i}{⩽}{5}}$$?
5、['算法与程序框图']正确率40.0%某医院今年$${{1}}$$月份至$${{6}}$$月份中,每个月为感冒来就诊的人数如下表所示:
| 月份 $${{i}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ | $${{6}}$$ |
| 因感冒就诊人数 | $${{a}_{1}}$$ | $${{a}_{2}}$$ | $${{a}_{3}}$$ | $${{a}_{4}}$$ | $${{a}_{5}}$$ | $${{a}_{6}}$$ |
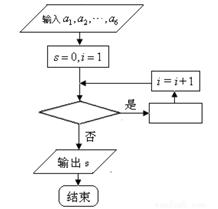
C
A.$$i < 6 ; ~ s=s+a_{i}$$
B.$$i \leqslant6 ; ~ s=a_{i}$$
C.$$i \leqslant6 ; ~ s=s+a_{i}$$
D.$$i > 6 ; \, \, s=a_{1}+a_{2}+\ldots+a_{i}$$
6、['算法与程序框图']正确率60.0%执行下面的程序框图,如果输入$$m=1 9 9 5, \; \; n=2 2 8$$,则计算机输出的数是()
B
A.$${{5}{8}}$$
B.$${{5}{7}}$$
C.$${{5}{6}}$$
D.$${{5}{5}}$$
7、['算法与程序框图']正确率60.0%如图是一个算法的程序框图,当输入值$${{x}}$$为$${{1}{0}}$$时,则其输出的结果是()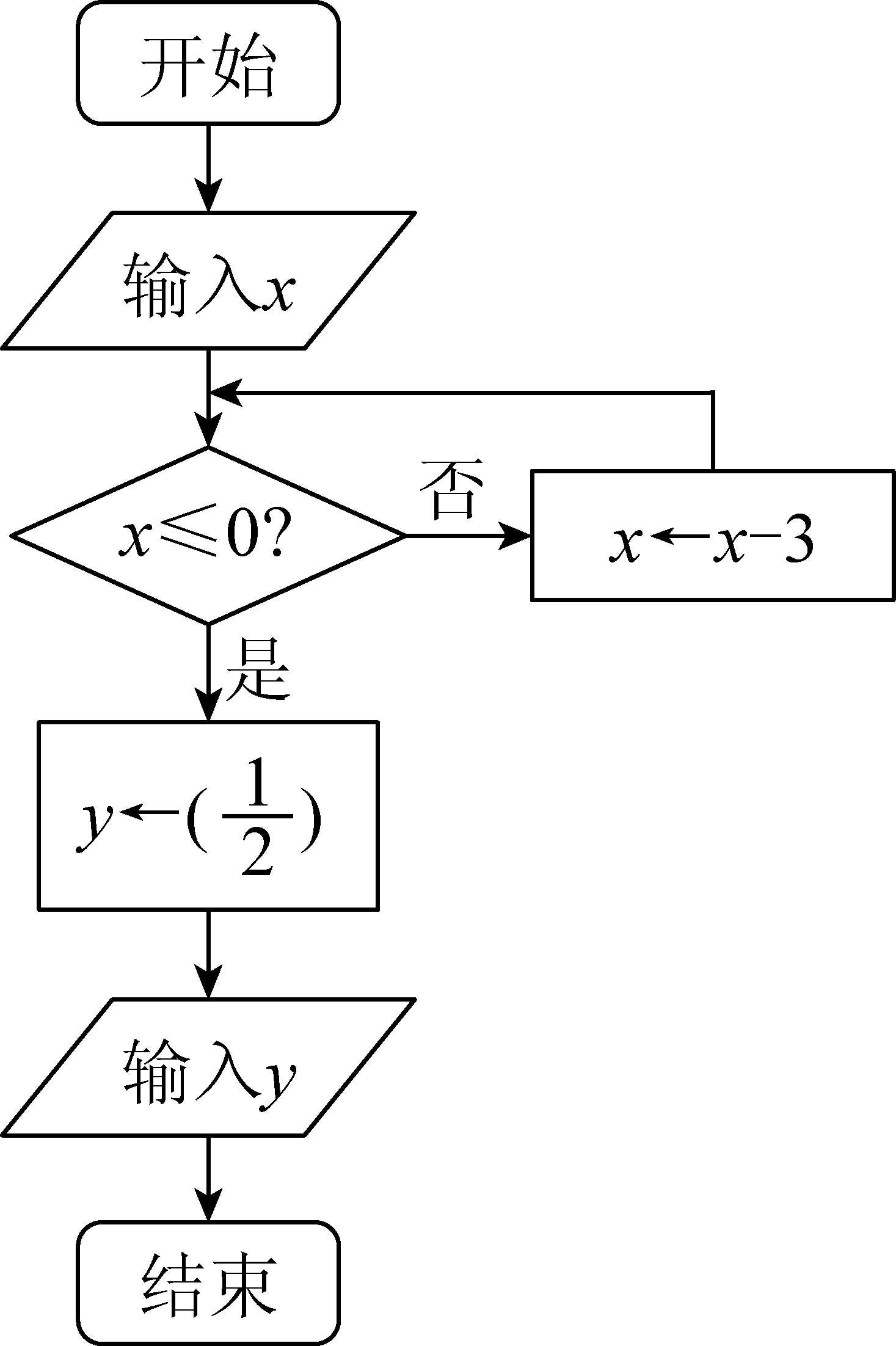
D
A.$$\frac{1} {2}$$
B.$${{2}}$$
C.$$\frac{1} {4}$$
D.$${{4}}$$
8、['算法与程序框图']正确率60.0%如图给出的是计算$$1+\frac1 3+\frac1 5+\cdots+\frac1 {2 0 1 7}$$的值的一个程序框图,则判断框内可以填入的条件是()
B
A.$${{i}{>}{{1}{0}{0}{8}}{?}}$$
B.$${{i}{⩽}{{1}{0}{0}{9}}{?}}$$
C.$${{i}{⩽}{{1}{0}{1}{0}}{?}}$$
D.$${{i}{<}{{1}{0}{1}{1}}{?}}$$
9、['定积分与微积分基本定理', '算法与程序框图']正确率60.0%已知$$a=\int_{0}^{\frac{\pi} {2}} \operatorname{s i n} x \mathrm{d} x$$,若执行如图所示的程序框图,则输出$${{k}}$$的值是()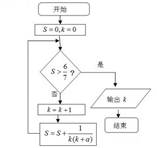
C
A.$${{5}}$$
B.$${{6}}$$
C.$${{7}}$$
D.$${{8}}$$
10、['算法与程序框图']正确率60.0%执行下面的程序框图,若输入$${{m}{=}{{7}{2}}}$$,$${{n}{=}{{3}{0}}}$$,则输出的$${{n}}$$的值为()
B
A.$${{1}{2}}$$
B.$${{6}}$$
C.$${{3}}$$
D.$${{0}}$$
1. 首先计算 $$( \sqrt{(-2 )^{2}} ) \times( \operatorname{l o g}_{\sqrt{2}} 4 )$$:
2. 程序框图输出 $$S = -2$$,需确定循环条件:
3. 程序框图输出结果为 15,需确定循环条件:
4. 二进制数 $$11111$$ 转换为十进制:
5. 统计 6 个月就诊人数总和的程序框图:
6. 输入 $$m=1995$$,$$n=228$$,程序框图实现辗转相除法求最大公约数:
7. 输入 $$x=10$$ 的程序框图逻辑:
8. 计算 $$1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{2017}$$ 的程序框图:
9. 已知 $$a = \int_{0}^{\frac{\pi}{2}} \sin x \, dx = 1$$,程序框图逻辑:
10. 输入 $$m=72$$,$$n=30$$,程序框图实现辗转相除法:
.jpg)