.jpg)
正确率40.0%随着科技的不断发展，人民消费水平的提升，手机购物逐渐成为消费的主流，当我们打开购物平台时，会发现其首页上经常出现我们喜欢的商品，这是电商平台推送的结果$${{.}}$$假设电商平台第一次给某人推送某商品，此人购买此商品的概率为$$\frac{2} {1 1}$$，从第二次推送起，若前一次不购买此商品，则此次购买的概率为$$\frac{1} {4}$$；若前一次购买了此商品，则此次仍购买的概率为$$\frac{1} {3}.$$记第$${{n}}$$次推送时不购买此商品的概率为$${{P}_{n}}$$，当$${{n}{⩾}{2}}$$时，$${{P}_{n}{⩽}{M}}$$恒成立，则$${{M}}$$的最小值为$${{(}{)}}$$
A.$$\frac{9 7} {1 3 2}$$
B.$$\frac{9 3} {1 3 2}$$
C.$$\frac{9 7} {1 2 0}$$
D.$$\frac{7 3} {1 2 0}$$
2、['二项分布与n重伯努利试验'， '直线与圆的位置关系及其判定']正确率40.0%已知圆$$x^{2}+y^{2}-2 x-8 y+1 3=0$$的圆心到直线$$k x+y-1=0 ( k \in{\bf Z} )$$的距离为$${{2}{\sqrt {2}}{，}}$$若$${{X}}$$$${{∼}}$$$$B \left( 4， \frac{1} {4} \right)，$$则$$P ( X=k )=$$（）
D
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\frac{3} {5}$$
C.$$\frac{1} {3}$$
D.$$\frac{2 7} {6 4}$$
3、['二项分布与n重伯努利试验'， '离散型随机变量的数字特征']正确率80.0%设随机变量$$X \sim B ( 1 0， p )$$，且满足$$D ( X )=2. 1$$，$$P ( X=4 ) < P ( X=6 )$$，则$${{p}{=}{(}{)}}$$
A.$${{0}{.}{7}}$$
B.$${{0}{.}{6}}$$
C.$${{0}{.}{4}}$$
D.$${{0}{.}{3}}$$
4、['二项分布与n重伯努利试验']正确率80.0%将一枚质地均匀的硬币连续抛掷$${{5}}$$次，至少连续出现$${{3}}$$次正面朝上的概率为（）
D
A.$$\frac{1} {4}$$
B.$$\frac{1} {3}$$
C.$$\frac{5} {3 2}$$
D.$$\frac{3} {1 6}$$
5、['二项分布与n重伯努利试验'， '相互独立事件的概率']正确率60.0%接种疫苗是预防和控制传染病最经济、有效的公共卫生干预措施.根据实验数据，人在接种某种病毒疫苗后，有$${{8}{0}{%}}$$的概率不会感染这种病毒，若有$${{4}}$$人接种了这种疫苗，则最多$${{1}}$$人被感染的概率为（）
A
A.$$\frac{5 1 2} {6 2 5}$$
B.$$\frac{2 5 6} {6 2 5}$$
C.$$\frac{1 1 3} {6 2 5}$$
D.$$\frac{1} {6 2 5}$$
6、['二项分布与n重伯努利试验'， '离散型随机变量的均值或数学期望'， '相互独立事件的概率']正确率40.0%某篮球队对队员进行考核，规则是：$${①}$$每人进行$${{3}}$$个轮次的投篮；$${②}$$每个轮次每人投篮$${{2}}$$次，若至少投中$${{1}}$$次，则本轮通过，否则不通过，已知队员甲投篮$${{1}}$$次投中的概率为$$\frac{2} {3}，$$如果甲各次投篮投中与否互不影响，那么甲$${{3}}$$个轮次通过的次数$${{X}}$$期望是（）
B
A.$${{3}}$$
B.$$\frac{8} {2}$$
C.$${{2}}$$
D.$$\frac{5} {3}$$
7、['二项分布与n重伯努利试验']正确率60.0%已知每次试验的成功概率为$$p < 0 < p < 1 )$$，重复进行试验直至第$${{n}}$$次才能得$$r \ ( 1 \leq r \leq n )$$次成功的概率为（）
B
A.$$C_{n}^{r} p^{r} \textsubscript{( 1-p )}^{n-r}$$
B.$$C_{n-1}^{r-1} p^{r} ~ ( 1-p )^{n-r}$$
C.$$p^{r} \ ( 1-p )^{n-r}$$
D.$$C_{n}^{r} p^{r-1} \， ( \mathbf{1}-p )^{\mathbf{\tiny3} n-r}$$
8、['二项分布与n重伯努利试验']正确率60.0%有一批种子，每一粒发芽的概率为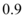
，播下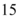
粒种子，恰有
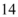粒发芽的概率为$${{(}{)}}$$
C
A.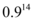
B.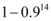
C.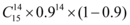
D.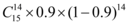
正确率60.0%设随机变量$$\xi\sim B ~ ( \ 2， \ p )$$，若$$P \ ( \xi\geq1 ) \ =\frac{5} {9}$$，则$${{p}}$$的值为（）
B
A.$$\frac{1} {4}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{1 6} {2 7}$$
10、['二项分布与n重伯努利试验']正确率60.0%在$${{4}}$$次独立重复试验中，事件$${{A}}$$发生的概率相同，若事件$${{A}}$$至少发生$${{1}}$$次的概率为$$\frac{6 5} {8 1}，$$则事件$${{A}}$$在$${{1}}$$次试验中发生的概率为（）
A
A.$$\frac{1} {3}$$
B.$$\frac{2} {5}$$
C.$$\frac{5} {6}$$
D.$$\frac{3} {4}$$
1. 首先，我们需要建立递推关系。设第$$n$$次不购买的概率为$$P_n$$，则购买的概率为$$1 - P_n$$。根据题意：
- 前一次不购买，则此次购买的概率为$$\frac{1}{4}$$，不购买的概率为$$\frac{3}{4}$$。
- 前一次购买，则此次仍购买的概率为$$\frac{1}{3}$$，不购买的概率为$$\frac{2}{3}$$。
2. 首先将圆的方程化为标准形式： $$x^2 - 2x + y^2 - 8y = -13$$ 配方得： $$(x-1)^2 + (y-4)^2 = 4$$ 圆心为$$(1,4)$$。直线$$kx + y -1 =0$$到圆心的距离为： $$\frac{|k \cdot 1 + 4 -1|}{\sqrt{k^2 +1}} = 2\sqrt{2}$$ 化简得： $$|k +3| = 2\sqrt{2} \sqrt{k^2 +1}$$ 平方后： $$k^2 +6k +9 = 8k^2 +8$$ 整理得： $$7k^2 -6k -1 =0$$ 解得： $$k =1$$或$$k = -\frac{1}{7}$$。由于$$k \in \mathbb{Z}$$，故$$k=1$$。