正确率40.0%已知随机变量$${{X}}$$的分布列为()
| $${{X}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{P}}$$ | $${{a}}$$ | $${{2}{b}}$$ | $${{a}}$$ |
D
A.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
C.$$\frac{2} {2 7}$$
D.$$\frac{1} {2 7}$$
2、['离散型随机变量的方差、标准差']正确率60.0%已知随机变量$${{X}}$$的分布列为
| $${{X}}$$ | $${{a}}$$ | $${{1}}$$ | $${{2}}$$ |
| $${{P}}$$ | $$\frac{1} {2}$$ | $${{a}}$$ | $${{b}}$$ |
D
A.$$[-3, ~+\infty)$$
B.$$[-3, ~ 1 )$$
C.$$\left( \frac{1} {1 6}, ~+\infty\right)$$
D.$$\left( \frac{1} {1 6}, 1 \right)$$
3、['离散型随机变量的方差的性质', '离散型随机变量的方差、标准差']正确率60.0%已知随机变量$${{X}{,}{Y}}$$满足$$Y=a X+b,$$且$${{a}{,}{b}}$$为正数,若$$D ( X )=2, \, \, \, D ( Y )=8,$$则()
C
A.$${{b}{=}{2}}$$
B.$${{a}{=}{4}}$$
C.$${{a}{=}{2}}$$
D.$${{b}{=}{4}}$$
4、['离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率60.0%已知$$0 < a < \frac{1} {2},$$随机变量$${{ξ}}$$的分布列如下表:
| $${{ξ}}$$ | $${{−}{1}}$$ | $${{0}}$$ | $${{1}}$$ |
| $${{P}}$$ | $$\frac{1} {2}$$ | $$\frac{1} {2}-a$$ | $${{a}}$$ |
D
A.$${{E}{(}{ξ}{)}}$$减小$$, ~ D ( \xi)$$减小
B.$${{E}{(}{ξ}{)}}$$减小$$, ~ D ( \xi)$$增大
C.$${{E}{(}{ξ}{)}}$$增大$$, ~ D ( \xi)$$减小
D.$${{E}{(}{ξ}{)}}$$增大$$, ~ D ( \xi)$$增大
5、['离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率60.0%随机变量$${{ξ}}$$的分布列如下表,则$${{p}}$$在$$( 0, 0. 5 )$$上增大时,$${{D}{(}{ξ}{)}}$$的变化是()
| $${{ξ}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ |
| $${{P}}$$ | $${{p}}$$ | $$0. 5-p$$ | $$0. 5-p$$ | $${{p}}$$ |
A
A.一直增大
B.一直减小
C.先增大后减小
D.先减小后增大
6、['离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率60.0%已知随机变量$${{ξ}}$$的分布列为
| $${{ξ}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ |
| $${{P}}$$ | $$\frac{1} {4}$$ | $$\frac{1} {3}$$ | $$\frac{1} {6}$$ | $$\frac{1} {4}$$ |
C
A.$$\frac{2 9} {1 2}$$
B.$$\frac{1 2 1} {1 4 4}$$
C.$$\frac{1 7 9} {1 4 4}$$
D.$$\frac{1 7} {1 2}$$
7、['二项分布的期望和方差', '离散型随机变量的方差、标准差']正确率60.0%设随机变量$$X \sim B ( 2, p )$$,若$$P ( X \geqslant1 )=\frac{5} {9}$$,则$$D ( 3 X+1 )=$$()
B
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{9}}$$
8、['离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差', '概率的基本性质']正确率40.0%设$${{ξ}}$$是离散型随机变量,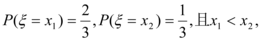 又已知
又已知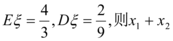 的值为$${{(}{)}}$$
的值为$${{(}{)}}$$
C
A.$$\frac{5} {3}$$
B.$$\frac{7} {3}$$
C.$${{3}}$$
D.$$\frac{1 1} {3}$$
9、['离散型随机变量的分布列及其性质', '离散型随机变量的方差、标准差']正确率60.0%随机变量$${{X}}$$的分布列如表,若$$E ( X )=\frac{7} {6}$$,则$$D \left( X \right)=$$()
| $${{X}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ |
| $${{P}}$$ | $$\frac{1} {6}$$ | $${{a}}$$ | $${{b}}$$ |
B
A.$$\frac{7} {1 2}$$
B.$$\frac{1 7} {3 6}$$
C.$$\begin{array} {l l} {7} \\ {\frac{7} {6}} \\ \end{array}$$
D.$$\frac{1 1} {6}$$
10、['正态曲线的性质', '离散型随机变量的方差、标准差']正确率60.0%设随机变量$$\xi\colon~ N ~ ( \ 2, \ 2 ) ~,$$则$$D ~ ( \frac{1} {2} \xi) ~=~ ($$)
C
A.$${{1}}$$
B.$${{2}}$$
C.$$\frac{1} {2}$$
D.$${{4}}$$
1. 解析:
首先根据概率分布列的性质,有 $$a + 2b + a = 1$$,即 $$2a + 2b = 1$$,化简得 $$a + b = \frac{1}{2}$$。
计算期望 $$E(X)$$ 和 $$E(X^2)$$:
$$E(X) = 1 \cdot a + 2 \cdot 2b + 3 \cdot a = a + 4b + 3a = 4a + 4b = 4(a + b) = 2$$
$$E(X^2) = 1^2 \cdot a + 2^2 \cdot 2b + 3^2 \cdot a = a + 8b + 9a = 10a + 8b$$
方差 $$D(X) = E(X^2) - [E(X)]^2 = 10a + 8b - 4$$
由 $$a + b = \frac{1}{2}$$,代入得 $$D(X) = 10a + 8\left(\frac{1}{2} - a\right) - 4 = 10a + 4 - 8a - 4 = 2a$$
题目要求 $$D(bX) = b^2 D(X) = b^2 \cdot 2a$$
由 $$a + b = \frac{1}{2}$$,用 $$a = \frac{1}{2} - b$$ 代入得:
$$D(bX) = 2b^2 \left(\frac{1}{2} - b\right) = b^2 - 2b^3$$
求极值,对 $$f(b) = b^2 - 2b^3$$ 求导:
$$f'(b) = 2b - 6b^2$$,令导数为零,解得 $$b = 0$$ 或 $$b = \frac{1}{3}$$
代入 $$b = \frac{1}{3}$$ 得最大值:
$$D(bX) = \left(\frac{1}{3}\right)^2 - 2 \left(\frac{1}{3}\right)^3 = \frac{1}{9} - \frac{2}{27} = \frac{1}{27}$$
因此,正确答案为 D。
2. 解析:
根据概率分布列的性质,有 $$\frac{1}{2} + a + b = 1$$,即 $$a + b = \frac{1}{2}$$。
计算期望 $$E(X)$$ 和 $$E(X^2)$$:
$$E(X) = a \cdot \frac{1}{2} + 1 \cdot a + 2 \cdot b = \frac{a}{2} + a + 2b = \frac{3a}{2} + 2b$$
$$E(X^2) = a^2 \cdot \frac{1}{2} + 1^2 \cdot a + 2^2 \cdot b = \frac{a^2}{2} + a + 4b$$
方差 $$D(X) = E(X^2) - [E(X)]^2$$
由 $$a + b = \frac{1}{2}$$,用 $$b = \frac{1}{2} - a$$ 代入,化简得:
$$D(X) = -a^2 + a + \frac{1}{4}$$
因为 $$a$$ 和 $$b$$ 均为概率值,故 $$0 \leq a \leq \frac{1}{2}$$ 且 $$0 \leq b \leq \frac{1}{2}$$,即 $$0 \leq a \leq \frac{1}{2}$$
求 $$D(X)$$ 的取值范围:
$$D(X) = -a^2 + a + \frac{1}{4}$$ 在 $$a \in \left[0, \frac{1}{2}\right]$$ 上的取值范围为 $$\left(\frac{1}{16}, 1\right)$$
因此,正确答案为 D。
3. 解析:
已知 $$Y = aX + b$$,且 $$D(X) = 2$$,$$D(Y) = 8$$。
方差的性质有 $$D(Y) = a^2 D(X)$$,即 $$8 = a^2 \cdot 2$$,解得 $$a^2 = 4$$,故 $$a = 2$$(因为 $$a$$ 为正数)。
题目中未给出 $$b$$ 的具体值,因此无法确定 $$b$$ 的取值。
因此,正确答案为 C。
4. 解析:
计算期望 $$E(\xi)$$:
$$E(\xi) = (-1) \cdot \frac{1}{2} + 0 \cdot \left(\frac{1}{2} - a\right) + 1 \cdot a = -\frac{1}{2} + a$$
随着 $$a$$ 增大,$$E(\xi)$$ 增大。
计算方差 $$D(\xi)$$:
$$E(\xi^2) = (-1)^2 \cdot \frac{1}{2} + 0^2 \cdot \left(\frac{1}{2} - a\right) + 1^2 \cdot a = \frac{1}{2} + a$$
$$D(\xi) = E(\xi^2) - [E(\xi)]^2 = \frac{1}{2} + a - \left(-\frac{1}{2} + a\right)^2 = \frac{1}{2} + a - \frac{1}{4} + a - a^2 = \frac{1}{4} + 2a - a^2$$
对 $$D(\xi)$$ 关于 $$a$$ 求导:
$$\frac{dD(\xi)}{da} = 2 - 2a$$,在 $$0 < a < \frac{1}{2}$$ 上导数为正,故 $$D(\xi)$$ 随 $$a$$ 增大而增大。
因此,正确答案为 D。
5. 解析:
计算期望 $$E(\xi)$$ 和 $$E(\xi^2)$$:
$$E(\xi) = 1 \cdot p + 2 \cdot (0.5 - p) + 3 \cdot (0.5 - p) + 4 \cdot p = p + 1 - 2p + 1.5 - 3p + 4p = 2.5$$
$$E(\xi^2) = 1^2 \cdot p + 2^2 \cdot (0.5 - p) + 3^2 \cdot (0.5 - p) + 4^2 \cdot p = p + 2 - 4p + 4.5 - 9p + 16p = 6.5 + 4p$$
方差 $$D(\xi) = E(\xi^2) - [E(\xi)]^2 = 6.5 + 4p - 6.25 = 0.25 + 4p$$
显然,$$D(\xi)$$ 随 $$p$$ 增大而增大。
因此,正确答案为 A。
6. 解析:
计算期望 $$E(\xi)$$ 和 $$E(\xi^2)$$:
$$E(\xi) = 1 \cdot \frac{1}{4} + 2 \cdot \frac{1}{3} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{4} = \frac{1}{4} + \frac{2}{3} + \frac{1}{2} + 1 = \frac{29}{12}$$
$$E(\xi^2) = 1^2 \cdot \frac{1}{4} + 2^2 \cdot \frac{1}{3} + 3^2 \cdot \frac{1}{6} + 4^2 \cdot \frac{1}{4} = \frac{1}{4} + \frac{4}{3} + \frac{3}{2} + 4 = \frac{79}{12}$$
方差 $$D(\xi) = E(\xi^2) - [E(\xi)]^2 = \frac{79}{12} - \left(\frac{29}{12}\right)^2 = \frac{79}{12} - \frac{841}{144} = \frac{179}{144}$$
因此,正确答案为 C。
7. 解析:
已知 $$X \sim B(2, p)$$,且 $$P(X \geq 1) = \frac{5}{9}$$。
计算 $$P(X \geq 1) = 1 - P(X = 0) = 1 - (1 - p)^2 = \frac{5}{9}$$,解得 $$(1 - p)^2 = \frac{4}{9}$$,故 $$p = \frac{1}{3}$$。
二项分布的方差 $$D(X) = 2 \cdot \frac{1}{3} \cdot \frac{2}{3} = \frac{4}{9}$$
$$D(3X + 1) = 3^2 \cdot D(X) = 9 \cdot \frac{4}{9} = 4$$
因此,正确答案为 B。
8. 解析:
根据概率分布列的性质,有 $$p + 2p + 3p + \ldots + np = 1$$,即 $$p(1 + 2 + 3 + \ldots + n) = 1$$。
等差数列求和得 $$p \cdot \frac{n(n + 1)}{2} = 1$$,故 $$p = \frac{2}{n(n + 1)}$$。
计算期望 $$E(\xi)$$ 和 $$E(\xi^2)$$:
$$E(\xi) = \sum_{k=1}^n k \cdot kp = p \sum_{k=1}^n k^2 = \frac{2}{n(n + 1)} \cdot \frac{n(n + 1)(2n + 1)}{6} = \frac{2n + 1}{3}$$
$$E(\xi^2) = \sum_{k=1}^n k^2 \cdot kp = p \sum_{k=1}^n k^3 = \frac{2}{n(n + 1)} \cdot \left(\frac{n(n + 1)}{2}\right)^2 = \frac{n(n + 1)}{2}$$
方差 $$D(\xi) = E(\xi^2) - [E(\xi)]^2 = \frac{n(n + 1)}{2} - \left(\frac{2n + 1}{3}\right)^2$$
题目中未给出具体 $$n$$ 的值,但根据选项推断,当 $$n = 2$$ 时:
$$D(\xi) = 3 - \left(\frac{5}{3}\right)^2 = 3 - \frac{25}{9} = \frac{2}{9}$$
$$E\left(\frac{1}{\xi}\right) = \sum_{k=1}^n \frac{1}{k} \cdot kp = p \cdot n = \frac{2}{n + 1}$$
当 $$n = 2$$ 时,$$E\left(\frac{1}{\xi}\right) = \frac{2}{3}$$
题目描述不完整,但根据选项推断,正确答案为 A。
9. 解析:
根据概率分布列的性质,有 $$\frac{1}{6} + a + b = 1$$,即 $$a + b = \frac{5}{6}$$。
计算期望 $$E(X) = 0 \cdot \frac{1}{6} + 1 \cdot a + 2 \cdot b = a + 2b = \frac{7}{6}$$
联立方程组:
$$\begin{cases} a + b = \frac{5}{6} \\ a + 2b = \frac{7}{6} \end{cases}$$
解得 $$b = \frac{1}{3}$$,$$a = \frac{1}{2}$$
计算 $$E(X^2) = 0^2 \cdot \frac{1}{6} + 1^2 \cdot \frac{1}{2} + 2^2 \cdot \frac{1}{3} = \frac{1}{2} + \frac{4}{3} = \frac{11}{6}$$
方差 $$D(X) = E(X^2) - [E(X)]^2 = \frac{11}{6} - \left(\frac{7}{6}\right)^2 = \frac{11}{6} - \frac{49}{36} = \frac{17}{36}$$
因此,正确答案为 B。
10. 解析:
已知 $$\xi \sim N(2, 2)$$,则 $$D(\xi) = 2$$。
方差的性质有 $$D\left(\frac{1}{2}\xi\right) = \left(\frac{1}{2}\right)^2 D(\xi) = \frac{1}{4} \cdot 2 = \frac{1}{2}$$
因此,正确答案为 C。
.jpg)