正确率40.0%随机变量$${{X}}$$的分布列为
| $${{X}}$$ | $${{−}{1}}$$ | $${{0}}$$ | $${{1}}$$ |
| $${{P}}$$ | $${{a}}$$ | $${{b}}$$ | $${{c}}$$ |
A
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\begin{array} {l l} {5} \\ {\frac{5} {9}} \\ \end{array}$$
C.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
D.$$\frac{3} {4}$$
2、['离散型随机变量的均值或数学期望', '相互独立事件的概率']正确率60.0%某人进行一项试验,若试验成功,则停止试验,若试验失败,则再重新试验一次,若试验$${{3}}$$次均失败,则放弃试验.若此人每次试验成功的概率均为$$\frac{2} {3},$$且各次试验成功与否互不影响,则此人试验次数$${{X}}$$的期望是()
B
A.$$\frac{4} {3}$$
B.$$\frac{1 3} {9}$$
C.$$\frac{5} {3}$$
D.$$\frac{1 3} {7}$$
3、['离散型随机变量的分布列及其性质', '离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率40.0%设$${{a}{,}{b}}$$为正数,且随机变量$${{X}}$$的分布列如下,则()
| $${{X}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ |
| $${{P}}$$ | $${{a}}$$ | $${{a}}$$ | $${{b}}$$ |
C
A.$${{E}{(}{X}{)}}$$有最大值$$, ~ D ( X )$$有最大值
B.$${{E}{(}{X}{)}}$$有最大值$$, ~ D ( X )$$无最大值
C.$${{E}{(}{X}{)}}$$无最大值$$, ~ D ( X )$$有最大值
D.$${{E}{(}{X}{)}}$$无最大值$$, ~ D ( X )$$无最大值
4、['均值与方差在决策问题中的应用', '离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率40.0%甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量$${{X}{,}{Y}{,}}$$已知甲、乙两名射手在每次射击中射中的环数都大于$${{6}{,}}$$且甲射中$$1 0, ~ 9, ~ 8, ~ 7$$环的概率分别为$$0. 5, ~ 0. 3, ~ 0. 1, ~ 0. 1,$$乙射中$$1 0, ~ 9, ~ 8$$环的概率分别为$$0. 3, ~ 0. 3, ~ 0. 2,$$则甲、乙的射击技术相比,()
A
A.甲的好
B.乙的好
C.一样好
D.无法比较
5、['二项分布的期望和方差', '离散型随机变量的均值或数学期望']正确率60.0%同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次试验成功,则在$${{2}}$$次试验中成功次数$${{X}}$$的均值是()
B
A.$${{1}}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$$\frac{3} {4}$$
D.$$\frac{1} {4}$$
6、['离散型随机变量的均值或数学期望']正确率80.0%甲$${、}$$乙两工人在同样的条件下生产某种产品,日产量相等,每天出废品的情况为
则有结论$${{(}{)}}$$
B
A.甲的产品质量比乙的产品质量好一些;
B.乙的产品质量比甲的产品质是好一些;
C.两人的产品质量一样好;
D.无法判断谁的质量好一些.
7、['离散型随机变量的均值或数学期望']正确率60.0%微信是现代生活进行信息交流的重要工具,随机对使用微信的$${{6}{0}}$$人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为$${{“}}$$微信达人$${{”}}$$,不超过两小时的人被定义为$${{“}}$$非微信达人$${{”}}$$,己知$${{“}}$$非微信达人$${{”}}$$与$${{“}}$$微信达人$${{”}}$$人数比恰为$${{3}{:}{2}}$$,为进一步了解使用微信对自己的日常工作和生活是否有影响,从这$${{6}{0}}$$个人中用分层抽样的方法抽取$${{1}{0}}$$人,若再从这$${{1}{0}}$$人中随机选取$${{3}}$$人进行问卷调查,设选取的$${{3}}$$人中$${{“}}$$微信达人$${{”}}$$的人数为$${{ξ}{,}}$$则$${{x}}$$的值和$${{ξ}}$$的数学期望分别是()
| 使用微信时间 (单位:小时) | 频数 | 频率 |
| $$( \; 0, \; \; 0. 5 ]$$ | $${{3}}$$ | $${{0}{.}{0}{5}}$$ |
| $$( \, 0. 5, \, 1 ]$$ | $${{x}}$$ | $${{p}}$$ |
| $$( 1, ~ 1. 5 ]$$ | $${{9}}$$ | $${{0}{.}{1}{5}}$$ |
| $$( \ 1. 5, \ 2 ]$$ | $${{1}{5}}$$ | $${{0}{.}{2}{5}}$$ |
| $$( \ 2, \ 2. 5 ]$$ | $${{1}{8}}$$ | $${{0}{.}{3}{0}}$$ |
| $$( \ 2. 5, \ 3 ]$$ | $${{y}}$$ | $${{q}}$$ |
| 合计 | $${{6}{0}}$$ | $${{1}{.}{0}{0}}$$ |
D
A.$$6 ; ~ ~ \frac{6} {5}$$
B.$$6 ; ~ ~ \frac{8} {5}$$
C.$$9 ; ~ \frac{8} {5}$$
D.$$9 ; ~ \frac{6} {5}$$
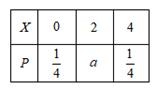
8、['离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率60.0%随机变量$${{X}}$$的分布列如表所示,则)
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
9、['离散型随机变量的均值或数学期望', '离散型随机变量的均值的性质']正确率60.0%已知随机变量$${{ξ}}$$满足$$E ( \xi)=2$$,则$$E ( 2 \xi+3 )=( \textit{} {} )$$
D
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{7}}$$
10、['二项分布的期望和方差', '离散型随机变量的均值或数学期望', '离散型随机变量的均值的性质']正确率40.0%为了响应国家发展足球的战略,哈市某校在秋季运动会中,安排了足球射门比赛.现有$${{1}{0}}$$名同学参加足球射门已知每名同学踢进的概率为$${{0}{.}{8}}$$,每名同学有$${{2}}$$次射门机会,且每次射门和同学之间都没有影响.现规定:踢进两个$${{1}{0}}$$分,踢进一个得$${{5}}$$分,一个未进得$${{0}}$$分,记$${{X}}$$为$${{1}{0}}$$个同学的得分总和,则$${{X}}$$的数学期望为()
D
A.$${{3}{0}}$$
B.$${{4}{0}}$$
C.$${{6}{0}}$$
D.$${{8}{0}}$$
1. 由于 $$a, b, c$$ 成等差数列,设公差为 $$d$$,则 $$b = a + d$$,$$c = a + 2d$$。由概率分布的性质,$$a + b + c = 1$$,代入得 $$3a + 3d = 1$$,即 $$a + d = \frac{1}{3}$$,故 $$b = \frac{1}{3}$$,$$a + c = \frac{2}{3}$$。
计算期望 $$E(X) = (-1) \cdot a + 0 \cdot b + 1 \cdot c = c - a$$。由于 $$a + c = \frac{2}{3}$$,$$c - a = \frac{2}{3} - 2a$$。
计算方差 $$D(X) = E(X^2) - [E(X)]^2 = a + c - (c - a)^2 = \frac{2}{3} - \left(\frac{2}{3} - 2a\right)^2$$。
为求最大值,令 $$f(a) = \frac{2}{3} - \left(\frac{2}{3} - 2a\right)^2$$,$$a \in \left[0, \frac{2}{3}\right]$$。当 $$a = \frac{1}{3}$$ 时,$$D(X)$$ 取得最大值 $$\frac{2}{3}$$。故选 A。
- $$P(X=1) = \frac{2}{3}$$
- $$P(X=2) = \frac{1}{3} \cdot \frac{2}{3} = \frac{2}{9}$$
- $$P(X=3) = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}$$
3. 由分布列性质,$$2a + b = 1$$,即 $$b = 1 - 2a$$。期望 $$E(X) = 0 \cdot a + 1 \cdot a + 2 \cdot b = a + 2(1 - 2a) = 2 - 3a$$。由于 $$a > 0$$ 且 $$b > 0$$,$$a \in \left(0, \frac{1}{2}\right)$$,$$E(X)$$ 无最大值。
方差 $$D(X) = E(X^2) - [E(X)]^2 = a + 4b - (2 - 3a)^2 = a + 4(1 - 2a) - (4 - 12a + 9a^2) = -9a^2 + 5a$$。当 $$a = \frac{5}{18}$$ 时,$$D(X)$$ 取得最大值 $$\frac{25}{36}$$。故选 C。
- 甲:$$E(X) = 10 \cdot 0.5 + 9 \cdot 0.3 + 8 \cdot 0.1 + 7 \cdot 0.1 = 9.2$$
- 乙:$$E(Y) = 10 \cdot 0.3 + 9 \cdot 0.3 + 8 \cdot 0.2 = 9.1$$
5. 单次试验成功的概率为 $$P = 1 - \left(\frac{1}{2}\right)^2 = \frac{3}{4}$$。两次试验成功次数 $$X$$ 服从二项分布 $$B(2, \frac{3}{4})$$,期望 $$E(X) = 2 \cdot \frac{3}{4} = \frac{3}{2}$$。故选 B。
- 甲:$$E(X) = 0 \cdot 0.4 + 1 \cdot 0.3 + 2 \cdot 0.2 + 3 \cdot 0.1 = 1$$
- 乙:$$E(Y) = 0 \cdot 0.3 + 1 \cdot 0.5 + 2 \cdot 0.2 = 0.9$$
7. 由题意,“非微信达人”与“微信达人”人数比为 3:2,故“微信达人”有 $$60 \cdot \frac{2}{5} = 24$$ 人,“非微信达人”有 36 人。由表格数据,$$y = 24 - 18 = 6$$,$$x = 36 - 3 - 9 - 15 = 9$$。
分层抽样中,“微信达人”占 $$\frac{24}{60} = \frac{2}{5}$$,故 10 人中有 4 名“微信达人”。$$ξ$$ 服从超几何分布,期望 $$E(ξ) = 3 \cdot \frac{4}{10} = \frac{6}{5}$$。故选 D。
又 $$D(X) = E(X^2) - [E(X)]^2 = 0.3 + 8m + 9n - (1.5 + n)^2$$。由 $$2m + n = 0.6$$,解得 $$D(X) = 1.5 + 4n - (1.5 + n)^2$$。当 $$n = 0.5$$ 时,$$D(X)$$ 取得最大值 1。故选 A。
9. 由期望线性性质,$$E(2ξ + 3) = 2E(ξ) + 3 = 2 \cdot 2 + 3 = 7$$。故选 D。
- $$P(Y=0) = (0.2)^2 = 0.04$$
- $$P(Y=5) = 2 \cdot 0.8 \cdot 0.2 = 0.32$$
- $$P(Y=10) = (0.8)^2 = 0.64$$
.jpg)