正确率60.0%已知随机变量$${{X}}$$的分布列为
| $${{X}}$$ | $${{−}{1}}$$ | $${{0}}$$ | $${{1}}$$ |
| $${{P}}$$ | $$\frac{1} {2}$$ | $$\frac{1} {6}$$ | $${{a}}$$ |
B
A.$$- \frac{1} {6}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$${{1}}$$
D.$$\frac{2 9} {3 6}$$
2、['离散型随机变量的分布列及其性质']正确率60.0%已知离散型随机变量$${{X}}$$的分布列为$$P \left( X=\frac{k} {5} \right)=a k ( k=1, \ 2, \ 3, \ 4, \ 5 ),$$则$$P \left( \frac{1} {1 0} < X < \frac{3} {5} \right)=$$()
C
A.$${{1}}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\frac{1} {5}$$
D.$$\frac{1} {3}$$
3、['离散型随机变量的分布列及其性质', '离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率60.0%随机变量$${{ξ}}$$的分布列如下表,若$$E ( \xi)=0,$$则$$D ( \xi)=$$()
| $${{ξ}}$$ | $${{−}{3}}$$ | $${{0}}$$ | $${{3}}$$ |
| $${{P}}$$ | $$\frac{1} {3}$$ | $${{a}}$$ | $${{b}}$$ |
A
A.$${{6}}$$
B.$${{2}}$$
C.$${{0}}$$
D.$${\sqrt {6}}$$
4、['古典概型的概率计算公式', '离散型随机变量的分布列及其性质', '组合的应用']正确率60.0%有$${{1}{0}}$$张卡片,其中$${{8}}$$张标有数字$${{2}{,}{2}}$$张标有数字$${{5}{,}}$$从中任意抽出$${{3}}$$张卡片,设$${{3}}$$张卡片上的数字和为$${{X}{,}}$$则$${{X}{⩾}{8}}$$的概率是()
C
A.$$\frac{4} {1 5}$$
B.$$\frac{7} {1 5}$$
C.$$\frac{8} {1 5}$$
D.$$\frac{3} {5}$$
5、['离散型随机变量的分布列及其性质']正确率60.0%设$${{ξ}}$$的分布列如下:
| $${{ξ}}$$ | $${{−}{1}}$$ | $${{0}}$$ | $${{1}}$$ |
| $${{P}_{i}}$$ | $$\frac{1} {2}$$ | $$\frac{1} {3}$$ | $${{p}}$$ |
则$${{p}}$$等于$${{(}{)}}$$
C
A.$${{0}}$$
B.$$\frac{1} {3}$$
C.$$\frac{1} {6}$$
D.不确定
6、['离散型随机变量的分布列及其性质', '离散型随机变量的均值或数学期望', '离散型随机变量的方差的性质']正确率40.0%已知随机变量$${{ξ}_{i}}$$满足$$P ~ ( \xi_{i}=0 ) ~=p_{i}, ~ P ~ ( \xi_{i}=1 ) ~=1-p_{i}$$,且$$0 < p_{i} < \frac{1} {2}, \, \, \, i=1, \, \, \, 2$$.若$$E ~ ( \xi_{1} ) ~ < E ~ ( \xi_{2} )$$,则()
B
A.$${{p}_{1}{<}{{p}_{2}}}$$,且$$D \ ( \xi_{1} ) \ < D \ ( \xi_{2} )$$
B.$${{p}_{1}{>}{{p}_{2}}}$$,且$$D \ ( \xi_{1} ) > D \ ( \xi_{2} )$$
C.$${{p}_{1}{<}{{p}_{2}}}$$,且$$D \ ( \xi_{1} ) > D \ ( \xi_{2} )$$
D.$${{p}_{1}{>}{{p}_{2}}}$$,且$$D \ ( \xi_{1} ) \ < D \ ( \xi_{2} )$$
7、['离散型随机变量的分布列及其性质']正确率60.0%设离散型随机变量$${{ξ}}$$的概率分布列如下,则下列各式中成立的是$${{(}{)}}$$
| | $${{−}{1}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{P}}$$ | $${{0}{.}{1}{0}}$$ | $${{a}}$$ | $${{0}{.}{1}{0}}$$ | $${{0}{.}{2}{0}}$$ | $${{0}{.}{4}{0}}$$ |
A
A.$$P ( \xi< 1. 5 )=0. 4$$
B.$$P ( \xi>-1 )=1$$
C.$$P ( \xi< 3 )=1$$
D.$$P ( \xi< 0 )=0$$
8、['离散型随机变量的分布列及其性质', '离散型随机变量的均值或数学期望']正确率60.0%某一随机变量$${{ξ}}$$的概率分布如下表,且$${{E}{{(}{ξ}{)}}{=}{{1}{.}{5}}}$$,则$${{m}{−}{n}}$$的值为$${{(}{)}}$$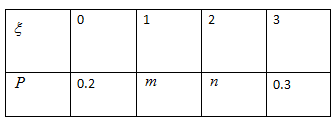
C
A.$${{−}{{0}{.}{3}}}$$
B.$${{0}{.}{1}}$$
C.$${{0}{.}{3}}$$
D.$${{−}{{0}{.}{1}}}$$
正确率40.0%从某班$${{6}}$$名学生(其中男生$${{4}}$$人,女生$${{2}}$$人)中任选$${{3}}$$人参加学校组织的社会实践活动.设所选$${{3}}$$人中女生人数为$${{ξ}{,}}$$则数学期望$${{E}{ξ}{=}{(}}$$)
B
A.$$\frac{4} {5}$$
B.$${{1}}$$
C.$$\frac{7} {5}$$
D.$${{2}}$$
10、['离散型随机变量的分布列及其性质', '离散型随机变量的均值或数学期望', '离散型随机变量的方差、标准差']正确率60.0%已知某离散型随机变量$${{X}}$$的分布列如下表,则随机变量$${{X}}$$的方差$${{D}{(}{X}{)}}$$等于()
| $${{X}}$$ | $${{0}}$$ | $${{1}}$$ |
| $${{P}}$$ | $${{m}}$$ | $${{2}{m}}$$ |
B
A.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
C.$$\frac{1} {3}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
1. 首先根据分布列的性质,所有概率之和为1,即 $$\frac{1}{2} + \frac{1}{6} + a = 1$$,解得 $$a = \frac{1}{3}$$。然后计算 $$E(X)$$:$$E(X) = (-1) \times \frac{1}{2} + 0 \times \frac{1}{6} + 1 \times \frac{1}{3} = -\frac{1}{6}$$。由于 $$Y = 2X + 1$$,利用期望的线性性质,$$E(Y) = 2E(X) + 1 = 2 \times (-\frac{1}{6}) + 1 = \frac{2}{3}$$。因此,正确答案是 B。
2. 首先根据分布列的性质,所有概率之和为1,即 $$\sum_{k=1}^{5} a k = a(1+2+3+4+5) = 15a = 1$$,解得 $$a = \frac{1}{15}$$。所求概率为 $$P\left(\frac{1}{10} < X < \frac{3}{5}\right) = P(X=\frac{1}{5}) + P(X=\frac{2}{5}) = \frac{1}{15} \times 1 + \frac{1}{15} \times 2 = \frac{1}{5}$$。因此,正确答案是 C。
3. 根据期望 $$E(\xi) = 0$$,有 $$(-3) \times \frac{1}{3} + 0 \times a + 3 \times b = 0$$,化简得 $$-1 + 3b = 0$$,解得 $$b = \frac{1}{3}$$。又因为概率之和为1,即 $$\frac{1}{3} + a + \frac{1}{3} = 1$$,解得 $$a = \frac{1}{3}$$。计算方差 $$D(\xi) = E(\xi^2) - [E(\xi)]^2 = (-3)^2 \times \frac{1}{3} + 0^2 \times \frac{1}{3} + 3^2 \times \frac{1}{3} - 0 = 6$$。因此,正确答案是 A。
4. 总的抽取方式数为 $$C_{10}^3 = 120$$。满足 $$X \geq 8$$ 的情况有两种:三张2(和为6,不满足)或两张2和一张5(和为9)。计算两张2和一张5的抽取方式数为 $$C_8^2 \times C_2^1 = 28 \times 2 = 56$$。因此概率为 $$\frac{56}{120} = \frac{7}{15}$$。正确答案是 B。
5. 根据分布列的性质,所有概率之和为1,即 $$\frac{1}{2} + \frac{1}{3} + p = 1$$,解得 $$p = \frac{1}{6}$$。因此,正确答案是 C。
6. 由题意,$$E(\xi_i) = 1 - p_i$$。因为 $$E(\xi_1) < E(\xi_2)$$,所以 $$1 - p_1 < 1 - p_2$$,即 $$p_1 > p_2$$。方差 $$D(\xi_i) = p_i(1 - p_i)$$,由于 $$0 < p_i < \frac{1}{2}$$,$$D(\xi_i)$$ 随 $$p_i$$ 增大而增大,因此 $$D(\xi_1) > D(\xi_2)$$。正确答案是 B。
7. 首先根据分布列的性质,$$0.10 + a + 0.10 + 0.20 + 0.40 = 1$$,解得 $$a = 0.20$$。选项分析:A. $$P(\xi < 1.5) = P(\xi = -1) + P(\xi = 0) + P(\xi = 1) = 0.10 + 0.20 + 0.10 = 0.40$$,正确;B. $$P(\xi > -1) = 1 - P(\xi = -1) = 0.90 \neq 1$$,错误;C. $$P(\xi < 3) = 1 - P(\xi = 3) = 0.60 \neq 1$$,错误;D. $$P(\xi < 0) = P(\xi = -1) = 0.10 \neq 0$$,错误。因此,正确答案是 A。
8. 根据分布列的性质,$$0.2 + n + 0.3 + m = 1$$,即 $$m + n = 0.5$$。又因为期望 $$E(\xi) = 0 \times 0.2 + 1 \times n + 2 \times 0.3 + 3 \times m = 1.5$$,化简得 $$n + 0.6 + 3m = 1.5$$,即 $$n + 3m = 0.9$$。联立解得 $$m = 0.2$$,$$n = 0.3$$,因此 $$m - n = -0.1$$。正确答案是 D。
9. 这是一个超几何分布问题,$$E(\xi) = n \times \frac{K}{N} = 3 \times \frac{2}{6} = 1$$。因此,正确答案是 B。
10. 根据分布列的性质,$$m + 2m = 1$$,解得 $$m = \frac{1}{3}$$。计算期望 $$E(X) = 0 \times \frac{1}{3} + 1 \times \frac{2}{3} = \frac{2}{3}$$,方差 $$D(X) = E(X^2) - [E(X)]^2 = 0^2 \times \frac{1}{3} + 1^2 \times \frac{2}{3} - \left(\frac{2}{3}\right)^2 = \frac{2}{3} - \frac{4}{9} = \frac{2}{9}$$。因此,正确答案是 B。
.jpg)