正确率60.0%甲乙两位游客慕名来到赣州旅游,准备分别从大余丫山、崇义齐云山、全南天龙山、龙南九连山和安远三百山$${{5}}$$个景点中随机选择其中一个,记事件$${{A}}$$:甲和乙选择的景点不同,事件$${{B}}$$:甲和乙恰好一人选择崇义齐云山,则条件概率$$P ( B \mid A )=$$()
B
A.$$\frac{1} {5}$$
B.$$\frac{2} {5}$$
C.$$\frac{9} {2 5}$$
D.$$\frac{9} {2 0}$$
2、['条件概率的应用']正确率60.0%面对全球爆发的疫情,我国第一时间向相关国家捐助医疗物资,并派出由医疗专家组成的医疗小组奔赴相关国家进行援助.现有$${{4}}$$个医疗小组甲、乙、丙、丁,和$${{4}}$$个需要援助的国家可供选择,每个医疗小组只去一个国家,设事件$${{A}}$$表示“$${{4}}$$个医疗小组去的国家各不相同”,事件$${{B}}$$表示“小组甲独自去一个国家”,则$$P ( A | B )=$$()
A
A.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{4} {9}} \\ \end{array}$$
D.$$\begin{array} {l l} {5} \\ {\frac{5} {9}} \\ \end{array}$$
3、['组合的应用', '条件概率的应用']正确率60.0%已知$${{6}}$$件产品中有$${{2}}$$件次品,今从中任取$${{2}}$$件,在已知其中一件是次品的前提下,另一件也是次品的概率为()
A
A.$$\frac{1} {1 5}$$
B.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
C.$$\frac{3} {5}$$
D.$$\frac{3} {1 0}$$
4、['随机事件发生的概率', '条件概率的应用']正确率60.0%袋子中装有大小、形状完全相同的$${{2}}$$个白球和$${{2}}$$个红球,现从中不放回地摸取$${{2}}$$个球,已知第二次摸到的是红球,则第一次摸到红球的概率为()
B
A.$$\frac{1} {6}$$
B.$$\frac{1} {3}$$
C.$$\frac{1} {2}$$
D.$$\frac{1} {5}$$
5、['互斥事件的概率加法公式', '条件概率的应用', '条件概率的概念及公式']正确率40.0%某射击小组有$${{5}{0}}$$名射手,其中一级射手$${{8}}$$人,二级射手$${{1}{6}}$$人,三级射手$${{2}{0}}$$人,四级射手$${{6}}$$人.在一场比赛中,一、二、三、四级射手能通过选拔进入初赛的概率分别为$$0. 9, ~ 0. 7, ~ 0. 6, ~ 0. 4$$.若从该射击小组随机选$${{1}}$$人参加比赛,则该选手能通过选拔进入初赛的概率为().
A
A.$$0. 6 5 6$$
B.$$0. 2 3 6$$
C.$$0. 3 4 6$$
D.$$0. 7 6 6$$
6、['古典概型的概率计算公式', '古典概型的应用', '有限样本空间', '条件概率的应用', '条件概率的概念及公式']正确率60.0%现抛掷两枚骰子,记事件$${{A}}$$为$${{“}}$$朝上的$${{2}}$$个数之和为偶数$${{”}}$$,事件$${{B}}$$为$${{“}}$$朝上的$${{2}}$$个数均为偶数$${{”}}$$,则$$P ( B | A ) {=} ( \qquad)$$
D
A.$$\frac{1} {8}$$
B.$$\frac{1} {4}$$
C.$$\frac{2} {5}$$
D.$$\frac{1} {2}$$
7、['事件的独立性与条件概率的关系', '条件概率的应用', '条件概率的概念及公式']正确率60.0%小赵$${、}$$小钱$${、}$$小孙$${、}$$小李到$${{4}}$$个景点旅游,每人只去一个景点,设事件$${{A}{=}{“}{4}}$$个人去的景点不相同$${{”}}$$,事件$${{B}{=}{“}}$$小赵独自去一个景点$${{”}}$$,则$$P ( A | B )=\emptyset$$)
A
A.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{4} {9}} \\ \end{array}$$
D.$$\begin{array} {l l} {5} \\ {\frac{5} {9}} \\ \end{array}$$
8、['相互独立事件的概率', '事件的独立性与条件概率的关系', '条件概率的应用']正确率60.0%三个元件$$T_{1}, ~ T_{2}, ~ T_{3}$$正常工作的概率分别为$$\frac{1} {2}, \frac{3} {4}, \frac{3} {4}$$且是互相独立的,按图中方式接入电路,电路正常工作的概率是$${{(}{)}}$$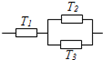
C
A.$$\frac{7} {3 2}$$
B.$$\frac{9} {3 2}$$
C.$$\frac{1 5} {3 2}$$
D.$$\frac{1 7} {3 2}$$
9、['古典概型的应用', '条件概率的应用']正确率40.0%$$\omega A T M^{\prime\prime}$$自动取款机设定:一张银行卡一天最多允许有三次输入错误,若第四次再错则自动将卡吞收一天晚上,李四在$$\omega A T M^{\prime\prime}$$自动取款机上取款,一时想不起该卡的密码,但可以确定是五个常用密码中的一个他第一次输入其中的一个密码是错误的,则他在确保不被吞卡的前提下取到款的概率是()
C
A.$$\frac{1} {5}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {2}$$
D.$$\frac{3} {4}$$
10、['条件概率的应用', '条件概率的概念及公式']正确率40.0%甲$${、}$$乙$${、}$$丙三人到三个不同的景点旅游,每人只去一个景点,设事件$${{A}}$$为$${{“}}$$三个人去的景点各不相同$${{”}}$$,事件$${{B}}$$为$${{“}}$$甲独自去一个景点,乙$${、}$$丙去剩下的景点$${{”}}$$,则$$P ( A | B )$$等于()
C
A.$$\begin{array} {l l} {\frac{4} {9}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
C.$$\frac{1} {2}$$
D.$$\frac{1} {3}$$
1. 首先计算事件$$A$$的概率$$P(A)$$。甲和乙选择的景点不同,甲有5种选择,乙有4种不同选择,总共有$$5 \times 4 = 20$$种情况。总的可能选择数为$$5 \times 5 = 25$$,因此$$P(A) = \frac{20}{25} = \frac{4}{5}$$。
接着计算事件$$B$$的概率$$P(B)$$。甲或乙中恰好一人选择崇义齐云山,有两种情况:甲选择崇义齐云山且乙选择其他景点,或乙选择崇义齐云山且甲选择其他景点。每种情况有$$1 \times 4 = 4$$种可能,总共有$$4 + 4 = 8$$种情况。因此$$P(B) = \frac{8}{25}$$。
条件概率$$P(B \mid A)$$表示在$$A$$发生的条件下$$B$$发生的概率,即$$P(B \mid A) = \frac{P(B)}{P(A)} = \frac{\frac{8}{25}}{\frac{4}{5}} = \frac{8}{25} \times \frac{5}{4} = \frac{2}{5}$$。
正确答案是$$B$$。
3. 已知其中一件是次品,总的可能情况为从6件中任取2件且至少一件是次品,即$$C(6,2) - C(4,2) = 15 - 6 = 9$$种。
另一件也是次品的情况为两件都是次品,有$$C(2,2) = 1$$种。
因此所求概率为$$\frac{1}{9}$$。
正确答案是$$B$$。
5. 该选手能通过选拔进入初赛的概率为各级射手概率的加权平均:
$$P = \frac{8}{50} \times 0.9 + \frac{16}{50} \times 0.7 + \frac{20}{50} \times 0.6 + \frac{6}{50} \times 0.4 = 0.144 + 0.224 + 0.24 + 0.048 = 0.656$$。
正确答案是$$A$$。
7. 事件$$B$$为小赵独自去一个景点,其他三人可以任意选择剩下的景点,有$$4 \times 3 \times 3 \times 3 = 108$$种情况。总的分配方式为$$4^4 = 256$$,因此$$P(B) = \frac{108}{256} = \frac{27}{64}$$。
事件$$A \cap B$$为四人去的景点各不相同且小赵独自去一个景点,有$$4 \times 3 \times 2 \times 1 = 24$$种情况,因此$$P(A \cap B) = \frac{24}{256} = \frac{3}{32}$$。
条件概率$$P(A \mid B) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{3}{32}}{\frac{27}{64}} = \frac{2}{9}$$。
正确答案是$$A$$。
9. 李四第一次输入错误,剩下四次尝试中最多三次错误。他有四个密码可选,其中只有一个正确。因此确保不被吞卡的概率为$$\frac{1}{4}$$。
正确答案是$$B$$。
.jpg)