正态分布及概率密度函数-7.5 正态分布知识点教师选题基础选择题自测题答案-湖南省等高三数学选择必修,平均正确率62.0%

1、['正态分布及概率密度函数']

正确率80.0%已知随机变量$${{ξ}}$$服从正态分布$$N \sim( \mu， \ \sigma^{2} )，$$若$$P ( \xi< 1 )=0. 1，$$$$P ( 1 \leqslant\xi\leqslant3 )=0. 8，$$则$${{μ}{=}}$$（）

A.$${{0}}$$

B.$${{1}}$$

C.$${{2}}$$

D.$${{3}}$$

2、['正态分布及概率密度函数']

正确率60.0%甲、乙两类水果的质量(单位：$${{k}{g}{)}}$$分别服从正态分布$${{N}{(}{{μ}_{1}}}$$，$${{σ}^{2}_{1}}$$$${{)}}$$，$${{N}{(}{{μ}_{2}}}$$，$${{σ}^{2}_{2}}$$$${{)}}$$，其正态曲线(正态密度函数为$${{φ}{_{μ}}}$$_，_$${{σ}}$$$${{(}{x}{)}{=}}$$$$\frac{1} {\sqrt{2 \pi} \sigma} e^{-\frac{( x-\mu)^{2}} {2 \sigma^{2}}}$$，$$x \in(-\infty$$，$${{+}{∞}{)}}$$如图所示，则下列说法不正确的是（）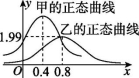
全品教育云平台：http://www.canpoint.cn

A.甲类水果的平均质量为$${{0}{.}{4}{{k}{g}}}$$

B.甲类水果的质量分布比乙类水果的质量分更集中于平均值左右

C.平均质量分布在$${{[}{{0}{.}{4}}}$$，$${{0}{.}{8}{]}}$$时甲类水果比乙类水果占比大

D.$${{σ}_{2}{=}{{1}{.}{9}{9}}}$$

3、['正态分布及概率密度函数'， '正态曲线的性质']

正确率60.0%若随机变量$${{ξ}}$$～$$N (-2， 4 )，$$则$${{ξ}}$$在区间$$(-4， ~-2 ]$$上取值的概率等于$${{ξ}}$$在下列哪个区间上取值的概率（）

A.$$( 2， 4 ]$$

B.$$( 0， 2 ]$$

C.$$[-2， 0 )$$

D.$$(-4， 4 ]$$

4、['正态分布及概率密度函数'， '正态曲线的性质']

正确率60.0%设随机变量$${{X}}$$～$$N ( \mu， \ \sigma^{2} )，$$且$$P ( X \leqslant C )=P ( X > C )=p，$$则$${{p}}$$的值为（）

A.$${{0}}$$

B.$${{1}}$$

C.$$\frac{1} {2}$$

D.$$\frac{1} {3}$$

5、['正态分布及概率密度函数']

正确率60.0%已知随机变量$$X \sim N ( 3， \sigma^{2} )$$，且$$P ( X > 4 )=0. 2 5$$，则$$P ( X \geqslant2 )=( \textit{} )$$

A.$${{0}{.}{2}{5}}$$

B.$${{0}{.}{3}{5}}$$

C.$${{0}{.}{7}{5}}$$

D.$${{0}{.}{6}{5}}$$

6、['正态分布及概率密度函数']

正确率60.0%在某项测量中，测量结果$${{ξ}}$$服从正态分布$$N ( 1， \sigma^{2} ) ( \sigma> 0 )$$，若$$P ( 0 < \xi< 1 )=0. 4$$，则$$P ( 0 < \xi< 2 )=$$

A.$${{0}{.}{4}}$$

B.$${{0}{.}{8}}$$

C.$${{0}{.}{6}}$$

D.$${{0}{.}{2}}$$

7、['正态分布及概率密度函数']

正确率60.0%设随机变量$$\xi\tilde{~} N ( 2， 9 )，$$若$$P ( \xi> c+3 )=P ( \xi< c-1 )$$，则实数$${{c}}$$的值为$${{(}{)}}$$

A.$${{1}}$$

B.$${{2}}$$

C.$${{3}}$$

D.$${{0}}$$

8、['正态分布及概率密度函数'， '正态曲线的性质']

正确率60.0%已知随机变量$$\xi\sim N ( 0， \sigma^{2} )，$$若$$P ( \xi> 2 )=0. 0 2 3$$，则$$P (-2 \leqslant\xi\leqslant2 )=( \textsubscript{\textit{h}} )$$

A.$$0. 9 7 7$$

B.$$0. 9 5 4$$

C.$$0. 6 2 8$$

D.$$0. 4 7 7$$

9、['正态分布及概率密度函数'， '二项分布与正态曲线'， '正态曲线的性质']

正确率60.0%在$${{2}{0}{1}{8}}$$年初的高中教师信息技术培训中，经统计，成都市高中教师的培训成绩$$X \sim N ( 8 5， 9 )$$，若已知$$P ( 8 0 < X \leqslant8 5 )=0. 3 5$$，则从成都高中教师中任选位教师，他的培训成绩大于$${{9}{0}}$$分的概率为

A.$${{0}{.}{8}{5}}$$

B.$${{0}{.}{6}{5}}$$

C.$${{0}{.}{3}{5}}$$

D.$${{0}{.}{1}{5}}$$

10、['正态分布及概率密度函数'， '正态曲线的性质']

正确率60.0%如果随机变量$$X-N \left(-1， \sigma^{2} \right)$$，且$$P \， (-3 \leqslant X \leqslant-1 )=0. 3$$，则$$P \left( X \geq1 \right)=\left( \begin{array} {c} {\mul} \\ \end{array} \right)$$

A.$${{0}{.}{4}}$$

B.$${{0}{.}{3}}$$

C.$${{0}{.}{2}}$$

D.$${{0}{.}{1}}$$

1. 解析：

根据正态分布的性质，$$P(\xi < 1) = 0.1$$，说明1位于均值左侧，且$$P(1 \leq \xi \leq 3) = 0.8$$，由于正态分布对称性，$$P(\xi \leq 1) = 0.1$$，$$P(\xi \leq 3) = 0.9$$。因此，均值$$\mu$$位于1和3的中点，即$$\mu = \frac{1 + 3}{2} = 2$$。答案为C。

2. 解析：

从图中可以看出，甲类水果的峰值在$$x=0.4$$处，故A正确；甲类曲线更陡峭，说明方差更小，质量分布更集中，B正确；在$$[0.4, 0.8]$$区间内，甲类曲线高于乙类，说明占比更大，C正确；图中无法直接得出$$\sigma_2 = 1.99$$，D不正确。答案为D。

3. 解析：

随机变量$$\xi \sim N(-2, 4)$$，均值为-2，方差为4。区间$$(-4, -2]$$关于均值对称的区间是$$[-2, 0)$$，因此概率相等。答案为C。

4. 解析：

由$$P(X \leq C) = P(X > C) = p$$，且$$P(X \leq C) + P(X > C) = 1$$，可得$$2p = 1$$，即$$p = \frac{1}{2}$$。答案为C。

5. 解析：

$$X \sim N(3, \sigma^2)$$，$$P(X > 4) = 0.25$$，由对称性，$$P(X < 2) = 0.25$$，因此$$P(X \geq 2) = 1 - 0.25 = 0.75$$。答案为C。

6. 解析：

$$\xi \sim N(1, \sigma^2)$$，$$P(0 < \xi < 1) = 0.4$$，由对称性，$$P(1 < \xi < 2) = 0.4$$，因此$$P(0 < \xi < 2) = 0.4 + 0.4 = 0.8$$。答案为B。

7. 解析：

$$\xi \sim N(2, 9)$$，由$$P(\xi > c+3) = P(\xi < c-1)$$，利用对称性，$$c+3$$和$$c-1$$关于均值2对称，即$$\frac{c+3 + c-1}{2} = 2$$，解得$$c = 1$$。答案为A。

8. 解析：

$$\xi \sim N(0, \sigma^2)$$，$$P(\xi > 2) = 0.023$$，由对称性，$$P(\xi < -2) = 0.023$$，因此$$P(-2 \leq \xi \leq 2) = 1 - 0.023 \times 2 = 0.954$$。答案为B。

9. 解析：

$$X \sim N(85, 9)$$，$$P(80 < X \leq 85) = 0.35$$，由对称性，$$P(85 < X \leq 90) = 0.35$$，因此$$P(X > 90) = 0.5 - 0.35 = 0.15$$。答案为D。

10. 解析：

$$X \sim N(-1, \sigma^2)$$，$$P(-3 \leq X \leq -1) = 0.3$$，由对称性，$$P(-1 \leq X \leq 1) = 0.3$$，因此$$P(X \geq 1) = 0.5 - 0.3 = 0.2$$。答案为C。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}