正确率60.0%在某区$${{2}{0}{2}{0}}$$年$${{5}}$$月份的高二期中质量检测考试中,学生的数学成绩$${{X}}$$服从正态分布$$N ( 9 8, ~ 1 0 0 )$$.已知参加本次考试的学生约有$${{9}{4}{5}{0}}$$人,如果某学生在这次考试中数学成绩为$${{1}{0}{8}}$$分,那么他的数学成绩排在该区的名次大约是()
A
A.$${{1}{4}{9}{8}}$$
B.$${{1}{6}{9}{8}}$$
C.$${{4}{5}{0}{0}}$$
D.$${{8}{0}{0}{0}}$$
2、['二项分布与正态曲线', '正态曲线的性质']正确率60.0%设两个正态分布$$N_{1} ~ ( \mu_{1}, \ \sigma_{1}^{2} )$$和$$N_{2} ~ ( \mu_{2}, \ \sigma_{2}^{2} )$$的密度函数曲线如图所示,则有()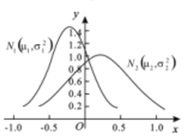
A
A.$$\mu_{1} < \mu_{2}, ~ ~ \sigma_{1} < \sigma_{2}$$
B.$$\mu_{1} < \mu_{2}, ~ ~ \sigma_{1} > \sigma_{2}$$
C.$$\mu_{1} > \mu_{2}, ~ ~ \sigma_{1} < \sigma_{2}$$
D.$$\mu_{1} > \mu_{2}, \, \, \, \sigma_{1} > \sigma_{2}$$
3、['二项分布与正态曲线', '正态曲线的性质']正确率60.0%设随机变量$${{X}}$$服从正态分布$$N ( 3, 4 )$$,若$$P ( X > c+4 )=P ( X < 5-2 c )$$,则$${{c}}$$等于$${{(}{)}}$$
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['标准正态分布', '二项分布与正态曲线', '正态曲线的性质']正确率60.0%在某校高三年级的高考全真模拟考试中,所有学生考试成绩的取值$${{X}{(}}$$单位:分)是服从正态分布$$N ~ ( \, 5 0 2, \, \, 1 4 4 )$$的随机变量,模拟$${{“}}$$重点控制线$${{”}}$$为$${{4}{9}{0}}$$分$${({{4}{9}{0}}}$$分及$${{4}{9}{0}}$$分以上都是重点),若随机抽取该校一名高三考生,则这位同学的成绩不低于$${{“}}$$重点控制线$${{”}}$$的概率为()
(附:若随机变量$${{X}}$$服从正态分布$$N ~ ( \mu, \ \sigma^{2} )$$,则
C
A.$$0. 6 8 2 6$$
B.$$0. 6 5 8 7$$
C.$$0. 8 4 1 3$$
D.$$0. 3 4 1 3$$
5、['二项分布与正态曲线', '正态曲线的性质']正确率60.0%已知随机变量$$X \! \sim\! ~ B ~ ( \mathrm{\boldmath~ 2, ~} ~ p ) ~, ~ Y \! \sim\! N ~ ( \mathrm{\boldmath~ 2, ~} ~ \sigma^{2} )$$,若$$P ~ ( X \geqslant1 ) ~=0. 3 6, ~ P ~ ( 0 < Y < 2 ) ~=p$$,则$$( Y > 4 ) ~=~$$()
C
A.$${{0}{.}{1}}$$
B.$${{0}{.}{2}}$$
C.$${{0}{.}{3}}$$
D.$${{0}{.}{4}}$$
6、['正态分布及概率密度函数', '二项分布与正态曲线', '正态曲线的性质']正确率60.0%已知随机变量$${{ζ}}$$服从正态分布$$N ( 3, \sigma^{2} )$$,则$$P ( \zeta< 3 )=( \mathrm{\ensuremath{~ )}}$$
D
A.$$\frac{1} {5}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {3}$$
D.$$\frac{1} {2}$$
7、['二项分布与正态曲线', '正态曲线的性质']正确率60.0%已知随机变量$${{X}}$$服从正态分布$$N \ ( a, \ 4 )$$,且$$P ~ ( X > 1 ) ~=0. 5, ~ P ~ ( X > 2 ) ~=0. 3, ~ P ~ ( X < 0 )$$等于()
B
A.$${{0}{.}{2}}$$
B.$${{0}{.}{3}}$$
C.$${{0}{.}{7}}$$
D.$${{0}{.}{8}}$$
8、['二项分布与正态曲线', '正态曲线的性质']正确率40.0% 在如图所示的正方形中随机投掷$$1 0 0 0 0$$
在如图所示的正方形中随机投掷$$1 0 0 0 0$$
C
A.$${{9}{0}{6}}$$
B.$${{2}{7}{1}{8}}$$
C.$$3 3 9. 7 5$$
D.$${{3}{4}{1}{3}}$$
9、['标准正态分布', '二项分布与正态曲线', '正态曲线的性质']正确率60.0%某厂生产的零件外直径$$X \sim N ( 8. 0, 0. 1 5^{2} ) ($$单位:$${{m}{m}{)}}$$,现从该厂上$${、}$$下午生产的零件中各随机取出一个,测得其外直径分别为$$7. 9 m m$$和$$7. 5 m m$$,则可认为()
C
A.上$${、}$$下午生产情况均为正常
B.上$${、}$$下午生产情况均为异常
C.上午生产情况正常,下午生产情况异常
D.上午生产情况异常,下午生产情况正常
10、['二项分布与正态曲线']正确率60.0%设$$X_{1} ~ \sim N ( \mu_{1}, \sigma_{1}^{2} ), ~ X_{2} \sim~ N ( \mu_{2}, \sigma_{2}^{2} ),$$其密度曲线如图所示,则有()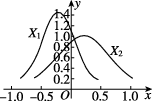
A
A.$$\mu_{1} < ~ \mu_{2}, ~ \sigma_{1} < ~ \sigma_{2}$$
B.$$\mu_{1} < ~ \mu_{2}, ~ \sigma_{1} > \sigma_{2}$$
C.$$\mu_{1} > \mu_{2}, ~ \sigma_{1} < ~ \sigma_{2}$$
D.$$\mu_{1} > \mu_{2}, \, \, \, \sigma_{1} > \sigma_{2}$$
1. 解析:
数学成绩 $$X \sim N(98, 100)$$,标准差 $$\sigma = 10$$。计算 $$108$$ 分的标准分数:$$Z = \frac{108 - 98}{10} = 1$$。查标准正态分布表,$$P(Z \leq 1) \approx 0.8413$$,因此 $$P(Z > 1) \approx 1 - 0.8413 = 0.1587$$。名次约为 $$9450 \times 0.1587 \approx 1498$$。故选 A。
2. 解析:
从图像可知,$$N_1$$ 的峰值在右侧,说明 $$\mu_1 > \mu_2$$;$$N_1$$ 的曲线更陡峭,说明 $$\sigma_1 < \sigma_2$$。故选 C。
3. 解析:
正态分布对称性要求 $$c+4$$ 和 $$5-2c$$ 关于均值 $$3$$ 对称:$$(c+4) + (5-2c) = 2 \times 3$$,解得 $$c = 3$$。故选 C。
4. 解析:
$$X \sim N(502, 144)$$,标准差 $$\sigma = 12$$。计算 $$490$$ 分的标准分数:$$Z = \frac{490 - 502}{12} = -1$$。$$P(X \geq 490) = P(Z \geq -1) \approx 0.8413$$。故选 C。
5. 解析:
由 $$X \sim B(2, p)$$,$$P(X \geq 1) = 1 - (1-p)^2 = 0.36$$,解得 $$p = 0.2$$。$$Y \sim N(2, \sigma^2)$$,$$P(0 < Y < 2) = 0.2$$,由对称性 $$P(Y > 4) = P(Y < 0) = 0.5 - 0.2 = 0.3$$。故选 C。
6. 解析:
正态分布 $$N(3, \sigma^2)$$ 的对称性要求 $$P(\zeta < 3) = 0.5$$。故选 D。
7. 解析:
$$X \sim N(a, 4)$$,$$P(X > 1) = 0.5$$ 说明均值 $$a = 1$$。$$P(X > 2) = 0.3$$,则 $$P(X < 0) = P(X > 2) = 0.3$$(对称性)。故选 B。
8. 解析:
题目不完整,无法解析。
9. 解析:
$$X \sim N(8.0, 0.15^2)$$,计算 $$7.9$$ 和 $$7.5$$ 的标准分数:$$Z_1 = \frac{7.9 - 8.0}{0.15} \approx -0.67$$(正常),$$Z_2 = \frac{7.5 - 8.0}{0.15} \approx -3.33$$(异常)。故选 C。
10. 解析:
从图像可知,$$X_1$$ 的峰值在右侧,说明 $$\mu_1 > \mu_2$$;$$X_1$$ 的曲线更平缓,说明 $$\sigma_1 > \sigma_2$$。故选 D。
.jpg)