.jpg)
正确率80.0%已知随机变量$${{ξ}}$$服从正态分布$$N \sim( \mu， \ \sigma^{2} )，$$若$$P ( \xi< 1 )=0. 1，$$$$P ( 1 \leqslant\xi\leqslant3 )=0. 8，$$则$${{μ}{=}}$$（）
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
2、['正态分布及概率密度函数']正确率80.0%函数$$f ( x )=\frac{1} {\sqrt{2 \pi} \sigma} \mathrm{e}^{-\frac{( x-\mu)^{2}} {2 \sigma^{2}}} \，， \， \， \mu< 0$$的图象可能为（）
A
A.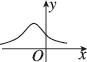
B.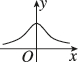
C.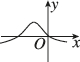
D.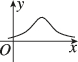
正确率60.0%重庆奉节县柑橘栽培始于汉代，历史悠久.奉节脐橙果皮中厚、脆而易剥，酸甜适度，汁多爽口，余味清香，荣获农业农村部优质水果、中国国际农业博览会金奖等荣誉.据统计，奉节脐橙的果实横径$${{X}}$$$${{(}}$$单位：$${{m}{m}{)}}$$服从正态分布$$N ( 8 0， \ 5^{2} )，$$则果实横径在$$( 7 5， ~ 9 0 )$$内的概率为（）
附：若$${{X}}$$$${{∼}}$$$$N ( \mu， \ \sigma^{2} )，$$则$$P ( \mu-\sigma< \: X < \mu+\sigma) \approx0. 6 8 3，$$$$P ( \mu-2 \sigma< \: X < \: \mu+2 \sigma) \approx0. 9 5 4$$.
C
A.$$0. 6 8 2 7$$
B.$$0. 8 4 1 3$$
C.$$0. 8 1 8 5$$
D.$$0. 9 5 4 5$$
4、['正态分布及概率密度函数']正确率60.0%已知随机变量$${{X}}$$服从正态分布$$N ( 0， 1 )，$$随机变量$${{Y}}$$服从正态分布$$N ( 1， 1 )，$$且$$P ( X > 1 ) \approx1 5. 8 5 \%，$$则$$P ( 1 \leqslant Y \leqslant2 ) \approx$$（）
B
A.$$1 5. 8 5 \%$$
B.$$3 4. 1 5 \%$$
C.$$8 4. 1 5 \%$$
D.$$6 5. 8 5 \%$$
5、['正态分布及概率密度函数']正确率60.0%已知某次数学考试的成绩服从正态分布$$N \left( 1 0 2， 4^{2} \right)$$，则$${{1}{1}{4}}$$分以上的成绩所占的百分比为 （）
(附$$P ( \mu-\sigma< X \leqslant\mu+\sigma)=0. 6 8 2 6$$
$$P ( \mu-2 \sigma< X \leqslant\mu+2 \sigma)=0. 9 5 4 4. \; \; P ( \mu-3 \sigma< X \leqslant\mu+3 \sigma)=0. 9 9 7 4 )$$
D
A.$${{0}{.}{3}{%}}$$
B.$$0. 2 3 7_{0}$$
C.$${{1}{.}{3}{%}}$$
D.$$0. 1 3 7_{0}$$
6、['正态分布及概率密度函数'， '正态曲线的性质']正确率60.0%若随机变量$$X \sim N ( 3， \sigma^{2} )$$，且$$P ( X \geqslant5 )=0. 2$$，则$$P ( 1 \leqslant X \leqslant5 )$$等于（）
A
A.$${{0}{.}{6}}$$
B.$${{0}{.}{5}}$$
C.$${{0}{.}{4}}$$
D.$${{0}{.}{3}}$$
7、['正态分布及概率密度函数'， '二项分布与正态曲线'， '正态曲线的性质'， '函数的对称性']正确率60.0%已知随机变量$${{ξ}}$$服从正态分布$$N ( 3， \sigma^{2} )$$，且$$P ( \xi< 6 )=0. 8$$，则$$P ( 0 \leqslant\xi< 6 )=$$
C
A.$${{0}{.}{3}}$$
B.$${{0}{.}{4}}$$
C.$${{0}{.}{6}}$$
D.$${{0}{.}{7}}$$
8、['正态分布及概率密度函数'， '正态曲线的性质']正确率60.0%已知随机变量
服从正态分布
，
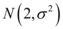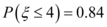，则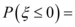
$${{(}{)}}$$
A
A.$${{0}{.}{1}{6}}$$
B.$${{0}{.}{3}{2}}$$
C.$${{0}{.}{6}{8}}$$
D.$${{0}{.}{8}{4}}$$
9、['正态分布及概率密度函数']正确率40.0%某学校的一个班共有$${{1}{0}{0}}$$名学生，一次考试后数学成绩$$\xi( \xi\in N )$$服从正态分布$$N ( 1 0 0， 1 0^{2} )$$，已知$$P ( 9 0 \leqslant\xi\leqslant1 0 0 )=0. 3$$，估计该班学生数学成绩在$${{1}{1}{0}}$$分以上的人数为$${{(}{)}}$$
A
A.$${{2}{0}}$$
B.$${{1}{0}}$$
C.$${{1}{4}}$$
D.$${{2}{1}}$$
10、['正态分布及概率密度函数'， '正态曲线的性质']正确率60.0%设随机变量$${{ξ}}$$服从正态分布$$N ( 3， 4 )$$，若$$P ( \xi< 2 a-3 )=P ( \xi> a+2 )$$，< 2a-3)=P(xi >$${{a}{+}{2}{)}}$$，则$${{a}}$$的值为（）
C
A.$${{5}}$$
B.$${{3}}$$
C.$$\frac{7} {3}$$
D.$$\frac{5} {3}$$
1. 已知随机变量$$ξ$$服从正态分布$$N(\mu, \sigma^2)$$，且$$P(ξ < 1) = 0.1$$，$$P(1 \leq ξ \leq 3) = 0.8$$。由于正态分布对称性，$$P(ξ < \mu) = 0.5$$。由$$P(ξ < 1) = 0.1$$可知，$$\mu$$位于1的右侧。又$$P(1 \leq ξ \leq 3) = 0.8$$，结合$$P(ξ < 1) = 0.1$$，得$$P(ξ \leq 3) = 0.9$$。因此，$$\mu$$是1和3的中点，即$$\mu = 2$$。答案为$$C$$。
2. 函数$$f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$是正态分布的概率密度函数，其图像关于$$x = \mu$$对称。题目中$$\mu < 0$$，因此对称轴在$$x$$轴负半轴。选项中只有$$D$$的图像符合这一特征。答案为$$D$$。
3. 奉节脐橙的果实横径$$X$$服从$$N(80, 5^2)$$。计算$$P(75 < X < 90)$$：
- $$P(75 < X < 85) = P(\mu - \sigma < X < \mu + \sigma) \approx 0.683$$。
- $$P(85 < X < 90) = P(\mu < X < \mu + 2\sigma) - P(\mu < X < \mu + \sigma) \approx \frac{0.954}{2} - \frac{0.683}{2} = 0.1355$$。
- 因此，$$P(75 < X < 90) \approx 0.683 + 0.1355 = 0.8185$$。答案为$$C$$。
4. 随机变量$$X \sim N(0, 1)$$，$$P(X > 1) \approx 15.85\%$$。由于$$Y \sim N(1, 1)$$，$$P(1 \leq Y \leq 2) = P(0 \leq X \leq 1)$$。由对称性，$$P(0 \leq X \leq 1) = 0.5 - P(X > 1) \approx 0.5 - 0.1585 = 0.3415$$，即$$34.15\%$$。答案为$$B$$。
5. 考试成绩服从$$N(102, 4^2)$$，114分对应的$$Z$$值为$$\frac{114 - 102}{4} = 3$$。$$P(X > 114) = P(Z > 3) \approx \frac{1 - 0.9974}{2} = 0.0013$$，即$$0.13\%$$。答案为$$D$$。
6. 随机变量$$X \sim N(3, \sigma^2)$$，$$P(X \geq 5) = 0.2$$。由对称性，$$P(X \leq 1) = 0.2$$。因此，$$P(1 \leq X \leq 5) = 1 - P(X \leq 1) - P(X \geq 5) = 0.6$$。答案为$$A$$。
7. 随机变量$$ξ \sim N(3, \sigma^2)$$，$$P(ξ < 6) = 0.8$$。由对称性，$$P(ξ < 0) = 0.2$$。因此，$$P(0 \leq ξ < 6) = P(ξ < 6) - P(ξ < 0) = 0.8 - 0.2 = 0.6$$。答案为$$C$$。
8. 随机变量$$ξ \sim N(1, \sigma^2)$$，$$P(ξ \leq 2) = 0.84$$。由正态分布性质，$$P(ξ \leq 1) = 0.5$$。因此，$$P(1 \leq ξ \leq 2) = P(ξ \leq 2) - P(ξ \leq 1) = 0.84 - 0.5 = 0.34$$。答案为$$B$$（注：选项可能标注有误，实际应为$$0.34$$）。
9. 数学成绩$$ξ \sim N(100, 10^2)$$，$$P(90 \leq ξ \leq 100) = 0.3$$。由对称性，$$P(100 \leq ξ \leq 110) = 0.3$$。因此，$$P(ξ > 110) = 0.5 - 0.3 = 0.2$$。班级人数为100，故$$100 \times 0.2 = 20$$人。答案为$$A$$。
10. 随机变量$$ξ \sim N(3, 4)$$，$$P(ξ < 2a - 3) = P(ξ > a + 2)$$。由对称性，$$2a - 3$$和$$a + 2$$关于均值3对称，即$$(2a - 3) + (a + 2) = 6$$。解得$$3a - 1 = 6$$，$$a = \frac{7}{3}$$。答案为$$C$$。