样本平均数与总体平均数-9.1 随机抽样知识点月考进阶选择题自测题答案-吉林省等高二数学必修,平均正确率57.99999999999999%

1、['方差与标准差'， '样本平均数与总体平均数']

正确率40.0%设样本数据$${{x}_{1}}$$，$${{x}_{2}}$$，$${{⋯}}$$，$$x_{2 0 2 1}$$的平均数为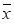 $\text{[math]}$ ，标准差为$${{s}}$$，若数据$${{2}{{x}_{1}}{+}{1}}$$，$${{2}{{x}_{2}}{+}{1}}$$，$${{⋯}}$$，$$2 x_{2 0 2 1}+1$$的平均数比标准差大$${{5}}$$，则$$\stackrel{\_} {x}^{2}+s$$的最小值为（）

A.$$- \frac{9} {4}$$

B.$$- \frac{1 7} {1 6}$$

C.$$\frac{6 3} {1 6}$$

D.$${{4}}$$

2、['样本平均数与总体平均数'， '一元线性回归模型']

正确率60.0%根据如图样本数据得到的回归方程为$$\hat{y}=b x+a，$$若样本点的中心为$$( \ 5， \ 0. 9 )$$．则当$${{x}}$$每增加$${{1}}$$个单位时，$${{y}}$$就（）

$${{x}}$$	$${{3}}$$	$${{4}}$$	$${{5}}$$	$${{6}}$$	$${{7}}$$
$${{y}}$$	$${{4}{.}{0}}$$	$${{a}{−}{{5}{.}{4}}}$$	$${{−}{{0}{.}{5}}}$$	$${{0}{.}{5}}$$	$${{b}{−}{{0}{.}{6}}}$$

A.增加$${{1}{.}{4}}$$个单位

B.减少$${{1}{.}{4}}$$个单位

C.增加$${{7}{.}{9}}$$个单位

D.减少$${{7}{.}{9}}$$个单位

3、['方差与标准差'， '样本平均数与总体平均数']

正确率60.0%设$$x_{1}=4， \， \， x_{2}=5， \， \， x_{3}=6$$，则该样本的标准差为（）

A.$$\frac{\sqrt{3}} {3}$$

B.$$\frac{\sqrt{6}} {3}$$

C.$$\frac{\sqrt{5}} {3}$$

D.$$\frac{\sqrt{7}} {3}$$

4、['方差与标准差'， '样本平均数与总体平均数']

正确率60.0%已知总体中各个体的值由小到大依次为 $\text{[math]}$ ，且总体的中位数为$${{1}{0}}$$，若要使该总体的方差最小，则$${{a}{，}{b}}$$的取值分别是（）

A.$${{9}{，}{{1}{1}}}$$

B.$${{1}{0}{，}{{1}{0}}}$$

C.$${{8}{，}{{1}{0}}}$$

D.$${{1}{0}{，}{{1}{1}}}$$

5、['样本平均数与总体平均数']

正确率80.0%从观测所得的数据中取出$${{m}}$$个$${{x}_{1}{，}{n}}$$个$${{x}_{2}{，}{p}}$$个$${{x}_{3}}$$组成一个样本，那么这个样本的平均数是（）

A.$$\frac{x_{1}+x_{2}+x_{3}} {3}$$

B.$$\frac{x_{1}+x_{2}+x_{3}} {m+n+p}$$

C.$$\frac{m x_{1}+n x_{2}+p x_{3}} {3}$$

D.$$\frac{m x_{1}+n x_{2}+p x_{3}} {m+n+p}$$

6、['样本平均数与总体平均数']

正确率80.0%期末考试结束后，为了了解某校高二年级$${{1}{{5}{0}{0}}}$$名学生的数学平均成绩，随机抽查了$${{5}{0}}$$名同学的成绩，得到他们数学成绩的平均数为$${{9}{0}{，}}$$则可估计该校高二年级学生数学成绩的平均数为（）

A.$${{9}{0}}$$

B.$${{9}{5}}$$

C.$${{8}{5}}$$

D.$${{9}{3}}$$

7、['线性回归模型的最小二乘法'， '样本平均数与总体平均数'， '一元线性回归模型']

正确率40.0%$${《}$$普通高中课程标准$${》}$$指出，学科核心素养是育人价值的集中体现，并提出了数学学科的六个核心素养．某机构为了解学生核心素养现状，对某地高中学生数学运算素养$${{x}}$$和数据分析素养$${{y}}$$进行量化统计分析，得到如下统计：

数学运算素养 $${{x}}$$	$${{2}}$$	$${{3}}$$	$${{4}}$$	$${{5}}$$	$${{6}}$$
数据分析素养 $${{y}}$$	$${{1}{.}{5}}$$	$${{4}{.}{5}}$$	$${{5}{.}{5}}$$	$${{6}{.}{5}}$$	$${{7}}$$

由表中数据，求得线性回归方程为$$\hat{y}=1. 3 x+\hat{a}，$$若某中学生的数学运算能力为$${{8}}$$，则该中学生的数据分析能力为$${{(}{)}}$$

A.$${{6}}$$

B.$${{6}{.}{3}}$$

C.$${{1}{0}{.}{2}}$$

D.$${{1}{0}{.}{6}}$$

8、['古典概型的概率计算公式'， '线性回归模型的最小二乘法'， '样本平均数与总体平均数'， '列举法']

正确率40.0%某研究机构在对具有线性相关的两个变量$${{x}{，}{y}}$$进行统计分析时，得到如下数据，由表中数据求得$${{y}}$$关于$${{x}}$$的回归方程为$$y=0. 7 x+a.$$则在这些样本中任取一点，该点落在回归直线下方的概率为

$${{x}}$$	$${{3}}$$	$${{5}}$$	$${{7}}$$	$${{9}}$$
$${{y}}$$	$${{1}}$$	$${{2}}$$	$${{4}}$$	$${{5}}$$

$${{(}{)}}$$

A.$$\frac{1} {4}$$

B.$$\frac{1} {2}$$

C.$$\frac{3} {4}$$

D.$${{0}}$$

9、['全称量词命题的否定'， '样本平均数与总体平均数'， '充分、必要条件的判定'， '方程组的解集']

正确率60.0%下列命题中是真命题的是（）
$$\oplus^{\iota\iota} x > 1^{\eta}$$是$${}^{\omega} x^{2} \geqslant1 "$$的充分不必要条件；
$${②}$$命题$${}^{\omega} \forall x > 0$$，都有 $\text{[math]}$ 的否定是$$\mathrm{` ` \exists~ x_0 ~ > 0 ~}$$，使得$$\operatorname{s i n} x_{0} > 1 " ;$$
$${③}$$数据$$x_{1}， x_{2}， \cdots， x_{8}$$的平均数为$${{6}}$$，则数据$$2 x_{1}-5， 2 x_{2}-5， \cdots， 2 x_{8}-5$$的平均数是$${{6}}$$；
$${④}$$当$${{a}{=}{−}{3}}$$时，方程组$$\left\{\begin{matrix} {3 x-2 y+1=0} \\ {a^{2} x-6 y=a} \\ \end{matrix} \right.$$有无穷多解.

A.$${①{②}{④}}$$

B.$${③{④}}$$

C.$${②{③}}$$

D.$${①{③}{④}}$$

10、['样本平均数与总体平均数']

正确率60.0%某地举行了一次数学竞赛，参加竞赛的$${{4}{0}}$$名学生的得分情况为：有$${{1}}$$人得$${{1}{0}}$$分，$${{3}}$$人得$${{9}}$$分，$${{8}}$$人得$${{8}}$$分，$${{1}{2}}$$人得$${{7}}$$分，$${{9}}$$人得$${{6}}$$分，$${{7}}$$人得$${{5}}$$分.则这$${{4}{0}}$$名学生的平均成绩是（）

A.$${{6}{.}{6}{8}}$$分

B.$${{6}{.}{8}{5}}$$分

C.$${{7}{.}{0}{5}}$$分

D.$${{7}{.}{1}{5}}$$分

1. 解析：

设样本数据$$x_1, x_2, \dots, x_{2021}$$的平均数为$$\bar{x}$$，标准差为$$s$$。变换后的数据$$2x_1+1, 2x_2+1, \dots, 2x_{2021}+1$$的平均数为$$2\bar{x}+1$$，标准差为$$2s$$。根据题意：

$$2\bar{x}+1 = 2s + 5$$，化简得$$\bar{x} = s + 2$$。

要求$$\bar{x}^2 + s$$的最小值，代入$$\bar{x} = s + 2$$得：

$$(s + 2)^2 + s = s^2 + 5s + 4$$。

这是一个关于$$s$$的二次函数，最小值在$$s = -\frac{5}{2}$$时取得，此时$$\bar{x} = -\frac{1}{2}$$。

代入得最小值为$$\left(-\frac{1}{2}\right)^2 + \left(-\frac{5}{2}\right) = -\frac{17}{16}$$。

答案为$$B$$。

2. 解析：

回归方程$$\hat{y} = bx + a$$的样本中心为$$(5, 0.9)$$，代入得$$0.9 = 5b + a$$。

根据表格数据计算$$x$$和$$y$$的平均值：

$$\bar{x} = \frac{3+4+5+6+7}{5} = 5$$，$$\bar{y} = \frac{4.0 + (a-5.4) + (-0.5) + 0.5 + (b-0.6)}{5} = 0.9$$。

化简得$$a + b = 7.9$$，结合回归方程得$$b = 1.4$$，$$a = -6.1$$。

回归方程为$$\hat{y} = 1.4x - 6.1$$，$$x$$每增加1个单位，$$y$$增加$$1.4$$个单位。

答案为$$A$$。

3. 解析：

样本数据$$x_1=4$$，$$x_2=5$$，$$x_3=6$$的平均数为$$\bar{x} = \frac{4+5+6}{3} = 5$$。

方差为$$s^2 = \frac{(4-5)^2 + (5-5)^2 + (6-5)^2}{3} = \frac{2}{3}$$。

标准差为$$s = \sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{3}$$。

答案为$$B$$。

4. 解析：

总体数据按从小到大排列为$$a, a, \dots, 10, b, b, \dots$$，中位数为$$10$$，说明$$a \leq 10 \leq b$$。

为使方差最小，$$a$$和$$b$$应尽量接近$$10$$，最优解为$$a = 10$$，$$b = 10$$。

答案为$$B$$。

5. 解析：

样本的平均数为加权平均：

$$\frac{mx_1 + nx_2 + px_3}{m+n+p}$$。

答案为$$D$$。

6. 解析：

样本的平均数为$$90$$，可直接估计总体平均数为$$90$$。

答案为$$A$$。

7. 解析：

根据表格数据计算$$\bar{x} = \frac{2+3+4+5+6}{5} = 4$$，$$\bar{y} = \frac{1.5+4.5+5.5+6.5+7}{5} = 5$$。

回归方程$$\hat{y} = 1.3x + \hat{a}$$过$$(4, 5)$$，代入得$$\hat{a} = 5 - 1.3 \times 4 = -0.2$$。

当$$x=8$$时，$$\hat{y} = 1.3 \times 8 - 0.2 = 10.2$$。

答案为$$C$$。

8. 解析：

根据表格数据计算$$\bar{x} = \frac{3+5+7+9}{4} = 6$$，$$\bar{y} = \frac{1+2+4+5}{4} = 3$$。

回归方程$$y = 0.7x + a$$过$$(6, 3)$$，代入得$$a = 3 - 0.7 \times 6 = -1.2$$。

回归方程为$$y = 0.7x - 1.2$$。计算各点的残差：

$$(3,1)$$：$$1 - (0.7 \times 3 - 1.2) = 0.1 > 0$$（在直线上方）；

$$(5,2)$$：$$2 - (0.7 \times 5 - 1.2) = -0.3 < 0$$（在直线下方）；

$$(7,4)$$：$$4 - (0.7 \times 7 - 1.2) = 0.3 > 0$$（在直线上方）；

$$(9,5)$$：$$5 - (0.7 \times 9 - 1.2) = -0.1 < 0$$（在直线下方）。

有2个点在直线下方，概率为$$\frac{2}{4} = \frac{1}{2}$$。

答案为$$B$$。

9. 解析：

①$$x > 1$$是$$x^2 \geq 1$$的充分不必要条件，正确；

②命题的否定正确；

③数据$$2x_i - 5$$的平均数为$$2 \times 6 - 5 = 7 \neq 6$$，错误；

④当$$a = -3$$时，方程组有无穷多解，正确。

答案为$$A$$。

10. 解析：

计算加权平均：

$$\frac{1 \times 10 + 3 \times 9 + 8 \times 8 + 12 \times 7 + 9 \times 6 + 7 \times 5}{40} = \frac{282}{40} = 7.05$$。

答案为$$C$$。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}