正确率80.0%简单随机抽样的结果()
B
A.完全由抽样方式所决定
B.完全由随机性所决定
C.完全由人为因素所决定
D.完全由计算方法所决定
2、['分层随机抽样的概念', '简单随机抽样的概念']正确率80.0%某高中为了解本校学生考入大学一年后的学习情况,对本校上一年考入大学的学生进行了调查,根据学生所属的专业类型,制成如图所示的扇形图.现从这些学生中抽出$${{1}{0}{0}}$$人进行进一步调查,已知张三为理学专业,李四为工学专业,则下列说法不正确的是()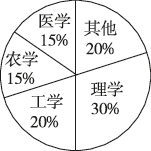
A
A.若按专业类型进行分层抽样,则张三被抽到的可能性比李四大
B.若按专业类型进行分层抽样,则理学专业和工学专业应分别抽取$${{3}{0}}$$人和$${{2}{0}}$$人
C.采用分层抽样比简单随机抽样更合理
D.该问题中的样本容量为$${{1}{0}{0}}$$
3、['分层随机抽样的概念', '简单随机抽样的概念']正确率80.0%要完成下列两项调查$${{:}{(}{1}{)}}$$江山社区有$${{1}{0}{0}}$$户高收入家庭,$${{2}{1}{0}{0}}$$户中等收入家庭,$${{9}{0}}$$户低收入家庭,从中抽取$${{2}{2}{9}}$$户调查有关消费购买力的某项指标;$${{(}{2}{)}}$$从光明中学高一年级的$${{2}{8}}$$名日语学生中抽取$${{3}}$$人调查学习情况$${{.}}$$应采用的抽样方法分别是()
C
A.$${{(}{1}{)}}$$用简单随机抽样,$${{(}{2}{)}}$$用分层随机抽样
B.$${{(}{1}{)}}$$用分层随机抽样,$${{(}{2}{)}}$$用其他抽样方法
C.$${{(}{1}{)}}$$用分层随机抽样,$${{(}{2}{)}}$$用简单随机抽样
D.$$( 1 ) ( 2 )$$都用分层随机抽样
4、['简单随机抽样的概念', '系统抽样']正确率40.0%某校为了了解高三学生平时的体育锻炼情况,从高三年级$${{1}{0}{4}{5}}$$名同学中抽取$${{5}{0}}$$名同学进行调查.先用简单随机抽样从$${{1}{0}{4}{5}}$$人中剔除$${{4}{5}}$$人,再按系统抽样方法从剩下的$${{1}{0}{0}{0}}$$人中抽取$${{5}{0}}$$人,则在这$${{1}{0}{4}{5}}$$人中,每个人被抽取的可能性()
C
A.都相等,且为$$\frac{1} {2 0}$$
B.不全相等
C.都相等,且为$$\frac{1 0} {2 0 9}$$
D.都不相等
5、['分层随机抽样的概念', '简单随机抽样的概念']正确率60.0%某工厂$$A, ~ B, ~ C$$三个车间共生产$${{2}{0}{0}{0}}$$个机器零件,其中$${{A}}$$车间生产$${{8}{0}{0}}$$个,$${{B}}$$车间生产$${{6}{0}{0}}$$个,$${{C}}$$车间生产$${{6}{0}{0}}$$个,要从中抽取一个容量为$${{5}{0}}$$的样本,记这项调查为$${①}$$,某学校高中一年级$${{1}{5}}$$名男篮运动员,要从中选出$${{3}}$$人参加座谈会,记这项调查为$${②}$$,则完成$${①{,}{②}}$$这两项调查宜采用的抽样方法依次是$${{(}{)}}$$.
B
A.分层抽样系统抽样
B.分层抽样简单随机抽样
C.系统抽样简单随机抽样
D.简单随机抽样分层抽样
6、['分层随机抽样的概念', '简单随机抽样的概念']正确率60.0%$${①}$$某小区有$${{4}{0}{0}{0}}$$人,其中少年人$${、}$$中年人$${、}$$老年人的比例为$$1_{:} ~ 2_{:} ~ 4$$,为了了解他们的体质情况,要从中抽取一个容量为$${{2}{0}{0}}$$的样本;$${②}$$从全班$${{4}{5}}$$名同学中选$${{5}}$$人参加校委会.
$${Ⅰ}$$.简单随机抽样法;$${Ⅱ}$$.系统抽样法;$${Ⅲ}$$.分层抽样法.
问题与方法配对正确的是()
A
A.
B.$$\textcircled{1} \mathrm{~ I}, \mathrm{~ \textcircled{2} \mathrm{~ I I} ~}$$
C.$$\textcircled{1} ~ \mathrm{I I}, ~ \textcircled{2} ~ \mathrm{I I}$$
D.$$\oplus\textrm{I I I} \left\{\begin{array} {l} {\oplus} \\ \end{array} \right. \textrm{I I}$$
7、['抽签法与随机数(表)法', '函数求值域', '简单随机抽样的概念']正确率60.0%将区间$$[ 0, 1 ]$$内的均匀随机数转化为$$[-2, 6 ]$$内的均匀随机数,需要采取的变换为()
D
A.$$a=6 a_{1}+2$$
B.$$a=6 a_{1}-2$$
C.$$a=8 a_{1}+2$$
D.$$a=8 a_{1}-2$$
8、['方差与标准差', '简单随机抽样的概念', '频率分布表与频率分布直方图', '频率分布直方图中的众数、中位数和平均数']正确率60.0%关于统计数据的分析,有以下几个结论:$${①}$$一组数不可能有两个众数$${{;}{②}}$$将一组数据中的每个数据都减去同一个数后,方差没有变化$${{;}{③}}$$调查剧院中观众的观看感受时,从$${{5}{0}}$$排$${{(}}$$每排人数相同$${{)}}$$中任意抽取一排的人进行调查,属于分层抽样$${{;}{④}}$$一组数据的方差一定是正数$${{;}{⑤}}$$如图所示是随机抽取的$${{2}{0}{0}}$$辆汽车通过某一段公路时的时速分布直方图,根据这个直方图,可以得到时速在$$[ 5 0, 6 0 ]$$的汽车大约是$${{6}{0}}$$辆.则这五种说法中错误的个数是()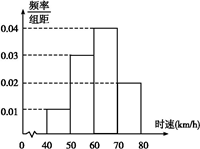
B
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
9、['抽签法与随机数(表)法', '简单随机抽样的概念']正确率60.0%某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将$${{5}{0}}$$个同学按进行编号,然后从随机数表第$${{9}}$$行第$${{1}{1}}$$列开始向右读,则选出的第$${{7}}$$个个体是$${{(}{)}}$$
(注:表为随机数表的第$${{8}}$$行和第$${{9}}$$行).
A
A.$${{0}{2}}$$
B.$${{1}{3}}$$
C.$${{4}{2}}$$
D.$${{4}{4}}$$
10、['分层随机抽样的概念', '简单随机抽样的概念']正确率60.0%要完成下列两项调查:
$${({1}{)}}$$某社区有$${{1}{0}{0}}$$户高收入家庭,$${{2}{1}{0}}$$户中等收入家庭,$${{9}{0}}$$户低收入家庭,从中抽取$${{1}{0}{0}}$$户调查消费购买力的某项指标;
$${({2}{)}}$$从某中学高二年级的$${{1}{0}}$$名体育特长生中抽取$${{3}}$$人调查学习负担情况.
应采取的抽样方法是()
C
A.$${({1}{)}}$$用系统抽样法,$${({2}{)}}$$用简单随机抽样法
B.$${({1}{)}}$$用分层抽样法,$${({2}{)}}$$用系统抽样法
C.$${({1}{)}}$$用分层抽样法,$${({2}{)}}$$用简单随机抽样法
D.$$( 1 ) \setminus( 2 )$$都用分层抽样法
1. 简单随机抽样的结果完全由随机性决定,因为每个个体被抽中的概率相等,不受人为或计算方法影响。正确答案是$$B$$。
3. 调查$$(1)$$中家庭收入差异明显,适合分层抽样;调查$$(2)$$中从$$28$$人中抽$$3$$人,适合简单随机抽样。正确答案是$$C$$。
5. 调查$$①$$中三个车间生产比例不同,适合分层抽样;调查$$②$$中从$$15$$人中选$$3$$人,适合简单随机抽样。正确答案是$$B$$。
7. 区间$$[0,1]$$变换到$$[-2,6]$$,需线性变换$$a = 8a_1 - 2$$(因为区间长度从$$1$$变为$$8$$,平移$$-2$$)。正确答案是$$D$$。
9. 从随机数表第$$9$$行第$$11$$列开始读取,依次为$$08, 02$$(第$$1$$个),$$01$$(第$$2$$个),$$14$$(第$$3$$个),$$07$$(第$$4$$个),$$02$$(重复跳过),$$13$$(第$$5$$个),$$42$$(第$$6$$个),$$44$$(第$$7$$个)。因此第$$7$$个是$$44$$,答案是$$D$$。
.jpg)