正确率80.0%某中学高一年级有$${{7}{1}{2}}$$名学生,其中男生有$${{3}{2}{6}}$$名,女生有$${{3}{8}{6}}$$名.现要抽取样本了解高一年级的平均身高,为减少“极端”样本的出现,你认为比较合适的抽样方法为()
C
A.抽签法
B.随机数表法
C.分层抽样
D.其他方法
2、['分层随机抽样的概念', '简单随机抽样的概念']正确率60.0%某工厂$$A, ~ B, ~ C$$三个车间共生产$${{2}{0}{0}{0}}$$个机器零件,其中$${{A}}$$车间生产$${{8}{0}{0}}$$个,$${{B}}$$车间生产$${{6}{0}{0}}$$个,$${{C}}$$车间生产$${{6}{0}{0}}$$个,要从中抽取一个容量为$${{5}{0}}$$的样本,记这项调查为$${①}$$,某学校高中一年级$${{1}{5}}$$名男篮运动员,要从中选出$${{3}}$$人参加座谈会,记这项调查为$${②}$$,则完成$${①{,}{②}}$$这两项调查宜采用的抽样方法依次是$${{(}{)}}$$.
B
A.分层抽样系统抽样
B.分层抽样简单随机抽样
C.系统抽样简单随机抽样
D.简单随机抽样分层抽样
3、['简单随机抽样的概念']正确率80.0%用简单随机抽样的方法从含有$${{1}{0}}$$个个体的总体中抽取一个容量为$${{3}}$$的样本,其中某一个体“第一次被抽到”的可能性与“第二次被抽到”的可能性分别是()
A
A.$$\frac{1} {1 0}, \, \, \frac{1} {1 0}$$
B.$$\frac{3} {1 0}, ~ \frac{1} {5}$$
C.$$\frac{1} {5}, ~ \frac{3} {1 0}$$
D.$$\frac{3} {1 0}, ~ \frac{3} {1 0}$$
4、['抽签法与随机数(表)法', '简单随机抽样的概念']正确率60.0%某个总体由编号为$$0 0 1, ~ 0 0 2, ~ \dots, 7 9 9, ~ 8 0 0$$的$${{8}{0}{0}}$$个个体组成,利用下面的随机数表选取$${{5}{0}}$$个个体,选取方法是从随机数表第$${{2}}$$行的第$${{4}}$$列数字开始由左到右依次选取,每行结束后紧接下一行,则选出来的第$${{4}}$$个个体的编号为$${{(}{)}}$$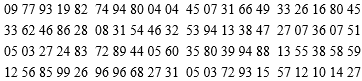
B
A.$${{1}{3}{3}}$$
B.$${{3}{2}{5}}$$
C.$${{3}{9}{4}}$$
D.$${{6}{0}{3}}$$
5、['抽签法与随机数(表)法', '简单随机抽样的概念']正确率60.0%总体是由编号为$$0 1, \ 0 2, \ \ldots, \ 1 9, \ 2 0$$的$${{2}{0}}$$个个体组成的,现用随机数法选取$${{5}}$$个个体,选取方法是从下面随机数表第$${{1}}$$行第$${{5}}$$列的数字开始由左向右依次选取两个数字,则选出来的第$${{5}}$$个个体的编号为
| $$7 8 \: 1 6 \: 6 5 \: 7 2 \: 0 8 \: 0 5 \: 6 3 \: 1 4 \: 0 7 \: 0 2 \: 4 3 \: 6 9 \: 9 7 \: 2 8 \: 0 1 \: 9 8$$ |
| |
B
A.$${{0}{1}}$$
B.$${{0}{2}}$$
C.$${{0}{4}}$$
D.$${{0}{7}}$$
正确率60.0%从某小学随机抽取$${{1}{0}{0}}$$名学生,将他们的身高(单位:厘米)分布情况汇总如下表:
| 身高 | $$( 1 0 0, \; 1 1 0 ]$$ | $$( 1 1 0, ~ 1 2 0 ]$$ | $$( 1 2 0, ~ 1 3 0 ]$$ | $$( 1 3 0, ~ 1 4 0 ]$$ | $$( 1 4 0, ~ 1 5 0 ]$$ |
| 频数 | $${{5}}$$ | $${{3}{5}}$$ | $${{3}{0}}$$ | $${{2}{0}}$$ | $${{1}{0}}$$ |
C
A.$$1 1 9. 3$$
B.$$1 1 9. 7$$
C.$$1 2 3. 3$$
D.$$1 2 6. 7$$
7、['简单随机抽样的概念', '随机事件发生的概率']正确率60.0%在$${{1}{0}}$$件同类型的产品中有$${{2}}$$件次品,现抽取$${{3}}$$件进行检验,每次抽取$${{1}}$$件,并且取出后不再放回,则取出的$${{3}}$$件产品中至少有$${{1}}$$件次品的概率为$${{(}{)}}$$
C
A.$$\frac{7} {1 0}$$
B.$$\frac{3} {5}$$
C.$$\frac{8} {1 5}$$
D.$$\frac{7} {1 5}$$
8、['简单随机抽样的概念', '散点图与正相关、负相关']正确率60.0%$$A, ~ B, ~ C, ~ D$$四名工人一天中生产零件的情况如图所示,每个点的横$${、}$$纵坐标分别表示该工人一天中生产的$${{I}}$$型$${、{I}{I}}$$型零件数,则下列说法错误的是()
D
A.四个工人中,$${{D}}$$的日生产零件总数最大
B.$${{A}{,}{B}}$$日生产零件总数之和小于$${{C}{,}{D}}$$日生产零件总数之和
C.$${{A}{,}{B}}$$日生产$${{I}}$$型零件总数之和小于$${{I}{I}}$$型零件总数之和
D.$$A, ~ B, ~ C, ~ D$$日生产$${{I}}$$型零件总数之和小于$${{I}{I}}$$型零件总数之和
9、['抽签法与随机数(表)法', '简单随机抽样的概念']正确率60.0%从$${{8}{0}{0}}$$件产品中抽取$${{6}{0}}$$件进行质检,利用随机数表法抽取样本时,先将$${{8}{0}{0}}$$件产品按进行编号.如果从随机数表第$${{8}}$$行第$${{8}}$$列的数$${{6}}$$开始往右读数(随机数表第$${{7}}$$行至第$${{9}}$$行的数如下$${{)}}$$,则抽取的第$${{4}}$$件产品的编号是$${{(}{)}}$$
$$8 1 0 5 0 1 0 8 0 5 \, 4 5 5 7 1 8 2 4 0 5 \, 3 5 3 0 3 4 2 8 1 4$$
$$6357332135 0532547048 9055857518$$
D
A.$${{6}{0}{2}}$$
B.$${{0}{2}{0}}$$
C.$${{5}{1}{6}}$$
D.$${{5}{6}{9}}$$
10、['古典概型的应用', '相互独立事件的概率', '简单随机抽样的概念']正确率60.0%袋中有红球$${、}$$黄球$${、}$$白球各$${{1}}$$个,每次任取一个,有放回地抽取$${{3}}$$次,则下列事件中概率是$$\frac{8} {9}$$的是()
B
A.颜色全相同
B.颜色不全相同
C.颜色全不同
D.颜色无红色
1. 题目要求减少“极端”样本的出现,因此应采用分层抽样(C),将男生和女生分开抽样以保证样本的代表性。
2. 调查①中,三个车间生产零件数量不同,应采用分层抽样;调查②中,从15人中选3人,适合简单随机抽样。因此选B。
3. 简单随机抽样中,每个个体每次被抽到的概率相同,均为$$ \frac{3}{10} $$,因此选D。
4. 从随机数表第2行第4列开始读取,依次跳过大于800和重复的数字,第4个有效编号为603,因此选D。
5. 从随机数表第1行第5列开始读取,依次选取在01-20范围内的数字,第5个有效编号为01,因此选A。
6. 中位数应在累计频数达到50的位置。计算得中位数落在(120,130]区间内,具体值为$$ 120 + \frac{50-40}{30} \times 10 \approx 123.3 $$,因此选C。
7. 计算补事件概率更简便:无次品的概率为$$ \frac{C_8^3}{C_{10}^3} = \frac{7}{15} $$,因此至少有1件次品的概率为$$ 1 - \frac{7}{15} = \frac{8}{15} $$,选C。
8. 通过坐标计算各工人的生产总数:A(15,20)、B(20,25)、C(30,20)、D(25,30)。验证选项C错误,因为A+B的I型总数35大于II型总数25。
9. 从随机数表第8行第8列开始读取,第4个有效编号为020,因此选B。
10. 颜色不全相同的概率为1减去全相同的概率$$ 1 - \frac{3}{27} = \frac{8}{9} $$,因此选B。
.jpg)