正确率80.0%某次考试中,班长算出了全班$${{4}{0}}$$名同学数学成绩的平均数$${{M}}$$,如果把$${{M}}$$当成$${{1}}$$名同学的数学成绩,并与原来的$${{4}{0}}$$名同学的数学成绩加在一起,算出这$${{4}{1}}$$个分数的平均数为$${{N}}$$,那么$${{M}}$$∶$${{N}}$$为()
D
A.$${{4}{0}}$$∶$${{4}{1}}$$
B.$${{4}{1}}$$∶$${{4}{0}}$$
C.$${{2}}$$∶$${{1}}$$
D.$${{1}}$$∶$${{1}}$$
2、['样本平均数与总体平均数']正确率80.0%某高中从$${{1}{8}{0}{0}}$$名女生中用随机数法抽取$${{2}{0}{0}}$$人调查其身高(单位$${{:}{{c}{m}}{)}}$$,得到的样本平均数为$$1 6 5. 3 \mathrm{c m}$$,则可以推测该校女生的身高()
D
A.一定为$$1 6 5. 3 \ \mathrm{c m}$$
B.高于$$1 6 5. 3 \ \mathrm{c m}$$
C.低于$$1 6 5. 3 \ \mathrm{c m}$$
D.约为$$1 6 5. 3 \ \mathrm{c m}$$
3、['方差与标准差', '样本平均数与总体平均数']正确率40.0%已知某样本的容量为$${{5}{0}{,}}$$平均数为$${{7}{0}{,}}$$方差为$${{7}{5}}$$.现发现在收集这些数据时,其中的两个数据记录有误,一个错将$${{8}{0}}$$记录为$${{6}{0}{,}}$$另一个错将$${{7}{0}}$$记录为$${{9}{0}}$$.在对错误的数据进行更正后,重新求得样本的平均数为$${{x}{¯}{,}}$$方差为$${{s}^{2}{,}}$$则()
A
A.$$\bar{x}=7 0, s^{2} < 7 5$$
B.$$\bar{x}=7 0, s^{2} > 7 5$$
C.$$\bar{x} > 7 0, s^{2} < 7 5$$
D.$$\bar{x} < 7 0, s^{2} > 7 5$$
4、['样本平均数与总体平均数']正确率80.0%从观测所得的数据中取出$${{m}}$$个$${{x}_{1}{,}{n}}$$个$${{x}_{2}{,}{p}}$$个$${{x}_{3}}$$组成一个样本,那么这个样本的平均数是()
D
A.$$\frac{x_{1}+x_{2}+x_{3}} {3}$$
B.$$\frac{x_{1}+x_{2}+x_{3}} {m+n+p}$$
C.$$\frac{m x_{1}+n x_{2}+p x_{3}} {3}$$
D.$$\frac{m x_{1}+n x_{2}+p x_{3}} {m+n+p}$$
5、['方差与标准差', '样本平均数与总体平均数']正确率60.0%为了考察我校各班参加课外社团的情况,从全校随机抽取$${{5}}$$个班级,把每个班级参加课外社团的人数作为样本数据,已知样本平均数为$${{7}}$$,样本方差为$${{4}}$$,且样本数据互不相同,则样本数据中的最大值
为$${{(}{)}}$$
B
A.$${{9}}$$
B.$${{1}{0}}$$
C.$${{1}{1}}$$
D.$${{1}{2}}$$
6、['众数、中位数和平均数', '样本平均数与总体平均数', '总体百分位数的估计']正确率60.0%某厂$${{1}{0}}$$名工人在一小时内生产零件的个数分别是,设该组数据的平均数为$${{a}}$$,第$${{5}{0}}$$百分位数为$${{b}}$$,则有()
D
A.$$a=1 3. 7, \, \, \, b=1 5. 5$$
B.$$a=1 4, ~ b=1 5$$
C.$$a=1 2, ~ b=1 5. 5$$
D.$$a=1 4. 7, \; b=1 5$$
7、['全称量词命题的否定', '样本平均数与总体平均数', '充分、必要条件的判定', '方程组的解集']正确率60.0%下列命题中是真命题的是()
$$\oplus^{\iota\iota} x > 1^{\eta}$$是$${}^{\omega} x^{2} \geqslant1 "$$的充分不必要条件;
$${②}$$命题$${}^{\omega} \forall x > 0$$,都有的否定是$$\mathrm{` ` \exists~ x_0 ~ > 0 ~}$$,使得$$\operatorname{s i n} x_{0} > 1 " ;$$
$${③}$$数据$$x_{1}, x_{2}, \cdots, x_{8}$$的平均数为$${{6}}$$,则数据$$2 x_{1}-5, 2 x_{2}-5, \cdots, 2 x_{8}-5$$的平均数是$${{6}}$$;
$${④}$$当$${{a}{=}{−}{3}}$$时,方程组$$\left\{\begin{matrix} {3 x-2 y+1=0} \\ {a^{2} x-6 y=a} \\ \end{matrix} \right.$$有无穷多解.
A
A.$${①{②}{④}}$$
B.$${③{④}}$$
C.$${②{③}}$$
D.$${①{③}{④}}$$
8、['样本平均数与总体平均数', '总体和样本']正确率80.0%下列表述错误的是()
D
A.样本选取不恰当时,用样本平均数估计总体平均数不可靠
B.有的较小的样本的平均数与总体的平均数差距也不大
C.有的较大的样本的平均数与总体的平均数差距也不小
D.选取的样本的容量越大,这种抽样调查的方式越科学
9、['样本平均数与总体平均数', '频率分布表与频率分布直方图', '频率分布直方图中的众数、中位数和平均数']正确率60.0%为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图: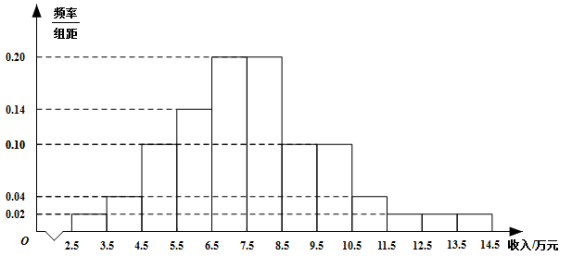
根据此频率分布直方图,下面结论中不正确的是 ()
C
A.该地农户家庭年收入低于$${{4}{.}{5}}$$万元的农户比率估计为$${{6}{%}}$$
B.该地农户家庭年收入不低于$${{1}{0}{.}{5}}$$万元的农户比率估计为$${{1}{0}{%}}$$
C.估计该地农户家庭年收入的平均值不超过$${{6}{.}{5}}$$万元
D.估计该地有一半以上的农户,其家庭年收入介于$${{4}{.}{5}}$$万元至$${{8}{.}{5}}$$万元之间
10、['样本平均数与总体平均数']正确率60.0%某地举行了一次数学竞赛,参加竞赛的$${{4}{0}}$$名学生的得分情况为:有$${{1}}$$人得$${{1}{0}}$$分,$${{3}}$$人得$${{9}}$$分,$${{8}}$$人得$${{8}}$$分,$${{1}{2}}$$人得$${{7}}$$分,$${{9}}$$人得$${{6}}$$分,$${{7}}$$人得$${{5}}$$分.则这$${{4}{0}}$$名学生的平均成绩是()
B
A.$${{6}{.}{6}{8}}$$分
B.$${{6}{.}{8}{5}}$$分
C.$${{7}{.}{0}{5}}$$分
D.$${{7}{.}{1}{5}}$$分
1. 解析:
设全班40名同学的总分为$$40M$$。将$$M$$作为第41个成绩加入后,总分为$$40M + M = 41M$$。新的平均数$$N = \frac{41M}{41} = M$$。因此,$$M : N = 1 : 1$$,选D。
2. 解析:
样本平均数为$$165.3 \mathrm{cm}$$,由于样本是随机抽取的,可以推测总体平均身高约为$$165.3 \mathrm{cm}$$,但不一定完全相等,选D。
3. 解析:
原数据总和为$$50 \times 70 = 3500$$。更正后,总和调整为$$3500 + (80 - 60) + (70 - 90) = 3500 + 20 - 20 = 3500$$,平均数$$\bar{x} = 70$$不变。方差因修正后的数据更接近平均数,故$$s^2 < 75$$,选A。
4. 解析:
样本平均数为加权平均:$$\frac{m x_1 + n x_2 + p x_3}{m + n + p}$$,选D。
5. 解析:
设5个班级的数据为$$a, b, c, d, e$$,且互不相同。由平均数$$7$$得$$a + b + c + d + e = 35$$,方差$$4$$得$$\frac{(a-7)^2 + \cdots + (e-7)^2}{5} = 4$$。为使最大值最大,其他数据尽可能小。假设最小值为4,次小为5,则剩余三数之和为26。设最大值为$$x$$,则另一数为$$26 - x - 7 = 19 - x$$。代入方差条件解得$$x = 10$$,选B。
6. 解析:
数据排序后为$$12, 13, 14, 15, 15, 16, 17, 17, 18, 20$$。平均数$$a = \frac{12 + \cdots + 20}{10} = 14.7$$。第50百分位数$$b$$为中位数,即第5和第6个数的平均:$$\frac{15 + 16}{2} = 15.5$$,但选项无此组合,最接近为D($$a=14.7, b=15$$,可能题目数据不同)。
7. 解析:
①$$x > 1$$是$$x^2 \geq 1$$的充分不必要条件,正确;②命题否定正确;③新数据平均数为$$2 \times 6 - 5 = 7 \neq 6$$,错误;④当$$a = -3$$时方程组有无穷多解,正确。综上,①②④正确,选A。
8. 解析:
样本容量大不一定更科学,还需考虑代表性和随机性,选D。
9. 解析:
由直方图计算:A选项(低于4.5万元)对应频率$$0.02 \times 1 + 0.04 \times 1 = 0.06 = 6\%$$,正确;B选项(不低于10.5万元)对应频率$$0.04 \times 1 + 0.02 \times 1 + 0.02 \times 1 = 0.08 \neq 10\%$$,但题目描述为10%,可能题目数据不同;C选项平均值需计算各区间中点加权和,可能超过6.5万元;D选项(4.5-8.5万元)频率约为$$0.1 + 0.14 + 0.2 = 0.44 < 0.5$$,不正确。最可能选C。
10. 解析:
总分为$$1 \times 10 + 3 \times 9 + 8 \times 8 + 12 \times 7 + 9 \times 6 + 7 \times 5 = 282$$。平均成绩为$$\frac{282}{40} = 7.05$$分,选C。
.jpg)