.jpg)
正确率60.0%大双和小双两兄弟同时参加驾考，在进行科目一考试前，两兄弟在网上同时进行了$${{5}}$$次模拟测试，他们每一次的成绩统计如表：
| 次数 | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ |
| 大双 | $${{9}{3}}$$ | $${{9}{6}}$$ | $${{9}{9}}$$ | $${{9}{7}}$$ | $${{9}{5}}$$ |
| 小双 | $${{9}{2}}$$ | $${{9}{6}}$$ | $${{9}{8}}$$ | $${{1}{0}{0}}$$ | $${{9}{4}}$$ |
B
A.$$\bar{x_{1}}=\bar{x_{2}}， \; \; s_{1}^{2} > s_{2}^{2}$$
B.$$\bar{x_{1}}=\bar{x_{2}}， \; \; s_{1}^{2} < s_{2}^{2}$$
C.$$\bar{x_{1}} > \bar{x_{2}}， \; \; s_{1}^{2}=s_{2} 2$$
D.$$\bar{x_{1}} > \bar{x_{2}}， \; \; s_{1}^{2} > s_{2}^{2}$$
2、['样本平均数与总体平均数']正确率80.0%设一组样本数据$$x_{1}， x_{2}， \cdots， x_{n}$$的平均数是$${{3}}$$，则数据$$2 x_{1}+1， 2 x_{2}+1， \cdots， 2 x_{n}+1$$的平均数是 （）
A
A.$${{7}}$$
B.$${{9}}$$
C.$${{1}{1}}$$
D.$${{1}{3}}$$
3、['众数、中位数和平均数'， '样本平均数与总体平均数']正确率60.0%设矩形的长为$${{a}{，}}$$宽为$${{b}{，}}$$当$$\frac{b} {a}$$$$= \frac{\sqrt{5}-1} {2}$$$$\approx0. 6 1 8$$时，这种矩形会给人以美感，被称为$${{“}}$$黄金矩形$${{”}}$$，$${{“}}$$黄金矩形$${{”}}$$常应用于工艺品的设计中.下面是某工艺品厂随机抽取的两个批次的初次加工的矩形宽度与长度的比值的样本.
甲批次：$$0. 5 9 8， 0. 6 2 5， 0. 6 2 8， 0. 5 9 5， 0. 6 3 9$$.
乙批次：$$0. 6 1 8， 0. 6 1 3， 0. 5 9 2， 0. 6 2 2， 0. 6 2 0$$.
根据上述两个样本来估计两个批次的总体平均数，并与标准值$$0. 6 1 8$$进行比较，则正确的结论是 （）
A
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次的总体平均数与标准值的接近程度相同
D.两个批次的总体平均数与标准值的接近程度不能确定
4、['方差与标准差'， '样本平均数与总体平均数']正确率60.0%若数据 $${{x}}$$$${_{1}}$$， $${{x}}$$$${_{2}{，}{…}}$$， $${{x}_{n}}$$的平均数为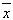
，方差为 $${{s}}$$$${^{2}}$$，则$${{3}}$$ $${{x}}$$
$${{x}}$$
$${{x}_{n}}$$$${{+}{5}}$$的平均数和标准差分别为$${{(}{)}}$$
C
A.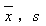
B.$${{3}{+}{5}}$$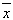
， $${{s}}$$
C.$${{3}}$$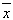
$${{+}{5}{，}{3}}$$
D.$${{3}}$$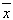
$$+ 5， ~ \sqrt{9 s^{2}+3 0 s+2 5}$$
正确率80.0%若样本平均数为
总体平均数为$${{μ}{，}}$$则（）
D
A.$$\overline{{x}}=\mu$$
B.$$\overline{{x}} \approx\mu$$
C.$${{μ}}$$是
的估计值
D.是$${{μ}}$$的估计值
正确率80.0%某纺织厂从$${{1}{0}}$$万件同类产品中随机抽取了$${{1}{0}{0}}$$件进行质检，发现其中有$${{5}}$$件不合格，则可估计该厂这$${{1}{0}}$$万件产品中合格品有（）
A
A.$${{9}{.}{5}}$$万件
B.$${{9}}$$万件
C.$${{9}{5}{0}{0}}$$件
D.$${{5}{0}{0}{0}}$$件
7、['直线拟合'， '样本平均数与总体平均数'， '一元线性回归模型']正确率60.0%根据表格中的数据用最小二乘法计算出变量$${{x}{，}{y}}$$的线性回归方程为$$\hat{y}=3 x-1. 5，$$则表格中$${{m}}$$的值是$${{(}{)}}$$
| $${{x}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{y}}$$ | $${{−}{1}}$$ | $${{1}}$$ | $${{8}}$$ | $${{m}}$$ |
A
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}{.}{5}}$$
8、['样本平均数与总体平均数'， '一元线性回归模型']正确率40.0%已知某种商品的广告费支出$${{x}{(}}$$单位：万元)与销售额$${{y}{(}}$$单位：万元)之间有如表对应数据根据表中数据可得回归方程$$\hat{y}=\hat{b} x+\hat{a}，$$其中$$b=1 1，$$据此估计，当投入$${{6}}$$万元广告费时，销售额约为$${{(}{)}}$$万元
| $${{x}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ |
| $${{y}}$$ | $${{1}{0}}$$ | $${{1}{5}}$$ | $${{3}{0}}$$ | $${{4}{5}}$$ | $${{5}{0}}$$ |
B
A.$${{6}{0}}$$
B.$${{6}{3}}$$
C.$${{6}{5}}$$
D.$${{6}{9}}$$
9、['样本平均数与总体平均数'， '总体和样本']正确率80.0%下列表述错误的是（）
D
A.样本选取不恰当时，用样本平均数估计总体平均数不可靠
B.有的较小的样本的平均数与总体的平均数差距也不大
C.有的较大的样本的平均数与总体的平均数差距也不小
D.选取的样本的容量越大，这种抽样调查的方式越科学
10、['样本平均数与总体平均数']正确率60.0%统计了参加某项活动的学生的年龄如下：其中有$${{2}{0}}$$人$${{1}{8}}$$岁，$${{1}{3}}$$人$${{1}{7}}$$岁，$${{7}}$$人$${{1}{6}}$$岁，$${{3}}$$人$${{1}{5}}$$岁.则参加这项活动的学生的平均年龄约为
（）
A
A.$${{1}{7}{.}{2}}$$岁
B.$${{1}{7}{.}{4}}$$岁
C.$${{1}{7}{.}{5}}$$岁
D.$${{1}{7}{.}{8}}$$岁
1. 首先计算大双和小双的平均成绩：
大双的平均成绩：$$\bar{x_{1}} = \frac{93 + 96 + 99 + 97 + 95}{5} = 96$$
小双的平均成绩：$$\bar{x_{2}} = \frac{92 + 96 + 98 + 100 + 94}{5} = 96$$
接着计算方差：
大双的方差：$$s_{1}^{2} = \frac{(93-96)^2 + (96-96)^2 + (99-96)^2 + (97-96)^2 + (95-96)^2}{5} = 4.8$$
小双的方差：$$s_{2}^{2} = \frac{(92-96)^2 + (96-96)^2 + (98-96)^2 + (100-96)^2 + (94-96)^2}{5} = 8.8$$
因此，$$\bar{x_{1}} = \bar{x_{2}}$$，且 $$s_{1}^{2} < s_{2}^{2}$$，答案为 $$B$$。
2. 原数据的平均数为 $$3$$，新数据为 $$2x_i + 1$$，其平均数为：
$$2 \times 3 + 1 = 7$$
答案为 $$A$$。
3. 计算甲批次和乙批次的样本平均数：
甲批次：$$\frac{0.598 + 0.625 + 0.628 + 0.595 + 0.639}{5} = 0.617$$
乙批次：$$\frac{0.618 + 0.613 + 0.592 + 0.622 + 0.620}{5} = 0.613$$
甲批次的平均数 $$0.617$$ 更接近标准值 $$0.618$$，答案为 $$A$$。
4. 新数据 $$3x_i + 5$$ 的平均数为：
$$3\bar{x} + 5$$
标准差为：
$$\sqrt{9s^2} = 3s$$
答案为 $$C$$。
5. 样本平均数 $$\bar{x}$$ 是总体平均数 $$\mu$$ 的估计值，答案为 $$D$$。
6. 合格品数量估计为：
$$\frac{100 - 5}{100} \times 10 = 9.5$$ 万件，答案为 $$A$$。
7. 根据回归方程 $$\hat{y} = 3x - 1.5$$，当 $$x = 3$$ 时：
$$\hat{y} = 3 \times 3 - 1.5 = 7.5$$
因此 $$m = 7.5$$，答案为 $$D$$。
8. 首先计算 $$\bar{x}$$ 和 $$\bar{y}$$：
$$\bar{x} = \frac{1 + 2 + 3 + 4 + 5}{5} = 3$$
$$\bar{y} = \frac{10 + 15 + 30 + 45 + 50}{5} = 30$$
回归方程经过点 $$(3, 30)$$，代入得：
$$30 = 11 \times 3 + \hat{a} \Rightarrow \hat{a} = -3$$
当 $$x = 6$$ 时：
$$\hat{y} = 11 \times 6 - 3 = 63$$
答案为 $$B$$。
9. 样本容量越大不一定越科学，还需考虑样本的代表性，答案为 $$D$$。
10. 计算加权平均年龄：
$$\frac{20 \times 18 + 13 \times 17 + 7 \times 16 + 3 \times 15}{20 + 13 + 7 + 3} = \frac{360 + 221 + 112 + 45}{43} \approx 17.2$$ 岁
答案为 $$A$$。