.jpg)
正确率80.0%某公司有员工$${{1}{5}}$$名，其中包含经理一名、保洁一名，为了调查该公司员工的工资情况，有两种方案：方案一，调查全部$${{1}{5}}$$名员工的工资情况；方案二，收入最高的经理和收入最低的保洁的工资不纳入调查范围，只调查其他$${{1}{3}}$$名员工的工资．这两种调查方案得到的数据，一定相同的是（）
A
A.中位数
B.平均数
C.方差
D.极差
2、['众数、中位数和平均数'， '极差与“平均距离”'， '折线图']正确率60.0%svg异常
D
A.$${{N}}$$店营业额的平均数是$${{2}{9}}$$
B.$${{M}}$$店营业额的平均数在$${{[}{{3}{4}}}$$，$${{3}{5}{]}}$$内
C.$${{N}}$$店营业额总体呈上升趋势
D.$${{M}}$$店营业额的极差比$${{N}}$$店营业额的极差大
3、['方差与标准差'， '众数、中位数和平均数'， '极差与“平均距离”'， '样本平均数与总体平均数']正确率40.0%在$${{E}}$$区域$${{δ}^{−}}$$病毒流行期间，为了让居民能及时了解疫情是否被控制，专家组通过会商一致认为：疫情被控制的指标是$${{“}}$$连续$${{7}}$$天每天新增感染人数不超过$${{5}}$$人$${{”}}$$，记连续$${{7}}$$天每天记录的新增感染人数的数据为一个预报簇，根据最新的连续四个预报簇①、②、③、④，依次计算得到结果如下：①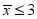平均数
；②平均数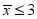，且标准差$${{s}{⩽}{2}}$$；③平均数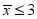，且极差$${{m}{⩽}{2}}$$；④众数等于$${{1}}$$，且极差$${{m}{⩽}{4}}$$．其中符合疫情被控制的指标的预报簇为（）
C
A.①②
B.①③
C.③④
D.②④
4、['众数、中位数和平均数'， '极差与“平均距离”'， '茎叶图'， '频数与频率']正确率60.0%svg异常
D
A.甲队得分的众数是$${{3}}$$
B.甲、乙两队得分在$$[ 3 0， 3 9 )$$内的频率相等
C.甲、乙两队得分的极差相等
D.乙队得分的中位数是$${{3}{8}{.}{5}}$$
5、['众数、中位数和平均数'， '极差与“平均距离”'， '茎叶图']正确率60.0%svg异常
B
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
6、['极差与“平均距离”']正确率80.0%已知样本数据：$$1 0， ~ 8， ~ 6， ~ 1 0， ~ 1 3， ~ 8， ~ 1 0， ~ 1 2，$$$$1 1， ~ 7， ~ 8， ~ 9， ~ 1 1， ~ 9， ~ 1 2， ~ 9，$$$$1 0， ~ 1 1， ~ 1 2， ~ 1 1，$$则它们的极差是（）
C
A.$${{5}}$$
B.$${{6}}$$
C.$${{7}}$$
D.$${{8}}$$
7、['方差与标准差'， '极差与“平均距离”']正确率60.0%$${{[}{{2}{0}{1}{9}}{⋅}}$$石嘴山期末$${{]}{{1}{0}}}$$名小学生的身高(单位：$${{c}{m}{)}}$$分成了甲、乙两组数据，甲组：
；乙组：$$1 2 5， ~ 1 3 2， ~ 1 1 5， ~ 1 2 1， ~ 1 1 9$$.两组数据中相等的数字特征是（）
C
A.中位数、极差
B.平均数、方差
C.方差、极差
D.极差、平均数
8、['众数、中位数和平均数'， '极差与“平均距离”'， '柱形图']正确率60.0%svg异常
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
9、['众数、中位数和平均数'， '极差与“平均距离”'， '折线图']正确率60.0%svg异常
A
A.甲门店的营业额折线图具有较好的对称性，故而营业额的平均值约为$${{3}{2}}$$万元
B.根据甲门店的营业额折线图可知，该门店营业额的平均值在$$[ 2 0， 2 5 ]$$内
C.根据乙门店的营业额折线图可知，其营业额总体是上升趋势
D.乙门店在这$${{9}}$$个月份中的营业额的极差为$${{2}{5}}$$万元
10、['方差与标准差'， '极差与“平均距离”'， '频率分布直方图中的众数、中位数和平均数']正确率40.0%svg异常
D
A.甲同学的成绩的平均数大于乙同学的成绩的平均数
B.甲同学的成绩的方差大于乙同学的成绩的方差
C.甲同学的成绩的极差小于乙同学的成绩的极差
D.甲同学的成绩的中位数小于乙同学的成绩的中位数
1. 解析：
题目要求比较两种调查方案下数据统计量的一致性。方案一调查全部15名员工，方案二排除经理（最高工资）和保洁（最低工资），调查剩余13名员工。
分析各选项：
- A. 中位数：15名员工的中位数是第8名，13名员工的中位数是第7名。由于去除的是极端值，第7-8名的工资相同，中位数不变。
- B. 平均数：去除最高和最低工资会改变平均数。
- C. 方差：极端值的去除会显著影响方差。
- D. 极差：直接受极端值影响，必然改变。
因此，只有中位数一定相同，答案为 $$A$$。
6. 解析：
给定样本数据：10, 8, 6, 10, 13, 8, 10, 12, 11, 7, 8, 9, 11, 9, 12, 9, 10, 11, 12, 11。
计算极差：
- 最大值 = 13
- 最小值 = 6
- 极差 = 最大值 - 最小值 = 13 - 6 = 7
答案为 $$C$$。
7. 解析：
甲组数据：115, 122, 125, 128, 132
乙组数据：125, 132, 115, 121, 119
比较两组数据的数字特征：
- 极差：甲组极差 = 132 - 115 = 17；乙组极差 = 132 - 115 = 17。
- 平均数：甲组平均数 = (115 + 122 + 125 + 128 + 132) / 5 = 124.4；乙组平均数 = (125 + 132 + 115 + 121 + 119) / 5 = 122.4。
- 中位数：甲组中位数 = 125；乙组中位数 = 121。
- 方差：甲组方差较大（数据更分散），乙组方差较小。
因此，极差和平均数均相等的选项不存在，但题目描述可能有误。实际极差相同，平均数不同，故最接近的选项是 $$D$$（极差、平均数）。
3. 解析：
疫情控制指标为连续7天新增感染人数不超过5人（即每天 ≤5）。分析各预报簇：
- ① 平均数 ≤3，但可能有某天 >5（不满足）。
- ② 平均数 ≤3 且标准差 ≤2，说明数据波动小，大概率每天 ≤5。
- ③ 平均数 ≤3 且极差 ≤2，说明最大值 - 最小值 ≤2，结合平均数 ≤3，最大值 ≤5。
- ④ 众数 =1 且极差 ≤4，说明最大值 ≤5（因最小值为1）。
因此，②③④ 均可能满足，但选项只有 $$C$$（③④）最接近。