.jpg)
正确率60.0%某地为践行“绿水青山就是金山银山”的人与自然和谐共生的发展理念，对该地企业已处理的废水进行实时监测．下表是对$${{A}{，}{B}}$$两家企业$${{1}{0}}$$天内已处理的废水的某项指标值的检测结果．下列说法正确的是（）
| $${{A}}$$ | $${{4}{3}}$$ | $${{7}{2}}$$ | $${{7}{3}}$$ | $${{9}{8}}$$ | $${{6}{3}}$$ | $${{8}{6}}$$ | $${{6}{5}}$$ | $${{7}{5}}$$ | $${{8}{1}}$$ | $${{7}{8}}$$ |
| $${{B}}$$ | $${{8}{2}}$$ | $${{6}{8}}$$ | $${{7}{1}}$$ | $${{3}{7}}$$ | $${{6}{1}}$$ | $${{6}{5}}$$ | $${{5}{8}}$$ | $${{6}{8}}$$ | $${{7}{7}}$$ | $${{9}{4}}$$ |
D
A.$${{A}}$$企业该指标值的极差较大
B.$${{A}}$$企业该指标值的中位数较小
C.$${{B}}$$企业该指标值的平均数较大
D.$${{B}}$$企业该指标值的众数与中位数相等
2、['众数、中位数和平均数'， '方差与标准差'， '极差与“平均距离”']正确率60.0%甲、乙、丙、丁四位同学组成的数学学习小组进行了一次小组竞赛，共测试了$${{5}}$$道题每题满分$${{2}{0}}$$分，每位同学各题得分情况如表：
| 题目 学生 | 第 $${{1}}$$ 题 | 第 $${{2}}$$ 题 | 第 $${{3}}$$ 题 | 第 $${{4}}$$ 题 | 第 $${{5}}$$ 题 |
| 甲 | $${{1}{0}}$$ | $${{1}{0}}$$ | $${{1}{0}}$$ | $${{2}{0}}$$ | $${{0}}$$ |
| 乙 | $${{1}{0}}$$ | $${{1}{0}}$$ | $${{5}}$$ | $${{1}{5}}$$ | $${{1}{0}}$$ |
| 丙 | $${{1}{0}}$$ | $${{1}{0}}$$ | $${{1}{5}}$$ | $${{1}{5}}$$ | $${{1}{0}}$$ |
| 丁 | $${{0}}$$ | $${{1}{0}}$$ | $${{1}{0}}$$ | $${{2}{0}}$$ | $${{2}{0}}$$ |
D
A.甲得分的平均数比丙得分的平均数大
B.乙得分的极差比丁得分的极差大
C.对于这$${{4}}$$位同学，因为第$${{4}}$$题得分的平均数比第$${{2}}$$题得分的平均数大，所以每位同学第$${{4}}$$题的相关知识一定比第$${{2}}$$题的相关知识掌握好
D.对于这$${{4}}$$位同学，第$${{3}}$$题得分的方差比第$${{5}}$$题得分的方差小
3、['众数、中位数和平均数'， '极差与“平均距离”']正确率80.0%$${{1}{6}}$$名参加百米半决赛的同学的成绩各不相同，按成绩取前$${{8}}$$名进入决赛.若小刘知道了自己的成绩后，要判断他能否进入决赛，则其他$${{1}{5}}$$名同学成绩的下列数据中，能使他得出结论的是（）
C
A.平均数
B.极差
C.中位数
D.以上都不对
4、['众数、中位数和平均数'， '方差与标准差'， '极差与“平均距离”']正确率60.0%某中学高三文科$${{2}}$$班在每周的星期一、三、五的晚自习前都要用半个小时进行英语听力测试，一共$${{3}{0}}$$个小题，每个小题$${{1}}$$分，共$${{3}{0}}$$分$${{.}}$$测试完后，该班英语老师都会随机抽取一个小组进行现场评阅，下表是该班英语老师在某个星期一随机抽取一个小组进行现场评阅的得分情况：
| 姓名 | 张周 | 邓靖川 | 王行 | 王沛 | 陆俊杰 | 刘振志 | 谭菲菲 | 任思颖 | 张韵 |
| 得分 (单位：分 $${{)}}$$ | $${{2}{0}}$$ | $${{2}{3}}$$ | $${{2}{2}}$$ | $${{2}{1}}$$ | $${{1}{4}}$$ | $${{1}{8}}$$ | $${{2}{0}}$$ | $${{2}{5}}$$ | $${{2}{6}}$$ |
①该小组英语听力测试分数的极差为$${{1}{2}}$$；
②该小组英语听力测试分数的中位数为$${{2}{1}}$$；
③该小组英语听力测试分数的平均数为$${{2}{1}}$$；
④该小组英语听力测试分数的方差为$${{1}{1}{.}}$$
其中说法正确的个数是（）
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
5、['方差与标准差'， '众数、中位数和平均数'， '极差与“平均距离”'， '样本平均数与总体平均数']正确率40.0%在$${{E}}$$区域$${{δ}^{−}}$$病毒流行期间，为了让居民能及时了解疫情是否被控制，专家组通过会商一致认为：疫情被控制的指标是$${{“}}$$连续$${{7}}$$天每天新增感染人数不超过$${{5}}$$人$${{”}}$$，记连续$${{7}}$$天每天记录的新增感染人数的数据为一个预报簇，根据最新的连续四个预报簇①、②、③、④，依次计算得到结果如下：①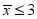平均数
；②平均数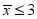，且标准差$${{s}{⩽}{2}}$$；③平均数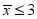，且极差$${{m}{⩽}{2}}$$；④众数等于$${{1}}$$，且极差$${{m}{⩽}{4}}$$．其中符合疫情被控制的指标的预报簇为（）
C
A.①②
B.①③
C.③④
D.②④
6、['众数、中位数和平均数'， '极差与“平均距离”'， '茎叶图']正确率60.0%svg异常
B
A.甲得分的中位数和极差都比乙大
B.甲得分的中位数比乙小，但极差比乙大
C.甲得分的中位数和极差都比乙小
D.甲得分的中位数比乙大，但极差比乙小
7、['极差与“平均距离”'， '折线图'， '柱形图']正确率60.0%svg异常
D
A.各季度供应规划建筑面积的最大值超过$${{2}{5}{0}{0}}$$万$${{m}^{2}}$$
B.各季度供应规划建筑而积的极差超过$${{1}{5}{0}{0}}$$万$${{m}^{2}}$$
C.$${{2}{0}{1}{9}}$$年各季度供应同比有增有减
D.$${{2}{0}{2}{0}}$$年第一季度与$${{2}{0}{1}{9}}$$年第一季度相比，供应同比下降幅度超过$${{1}{0}{%}}$$
8、['极差与“平均距离”'， '折线图']正确率60.0%svg异常
D
A.从$${{7}}$$月$${{2}}$$日到$${{7}}$$月$${{5}}$$日白天的平均气温呈下降趋势
B.这$${{1}{0}}$$天白天的平均气温的极差大于$${{6}{^{∘}}{C}}$$
C.这$${{1}{0}}$$天中白天的平均气温为$${{2}{6}{^{∘}}{C}}$$的频率最大
D.这$${{1}{0}}$$天中白天的平均气温大于$${{2}{6}{^{∘}}{C}}$$的有$${{5}}$$天
9、['极差与“平均距离”'， '折线图'， '柱形图']正确率60.0%svg异常
D
A.$${{2}{0}{1}{0}}$$年以来我国考研报名人数逐年增多
B.这$${{1}{1}}$$年来考研报名人数的极差超过$${{2}{6}{0}}$$万人
C.与上一年相比$${{2}{0}{1}{6}}$$年考研报名人数增速最慢
D.$${{2}{0}{1}{5}}$$年的报录比最低
10、['众数、中位数和平均数'， '极差与“平均距离”'， '折线图']正确率60.0%svg异常
A
A.甲门店的营业额折线图具有较好的对称性，故而营业额的平均值约为$${{3}{2}}$$万元
B.根据甲门店的营业额折线图可知，该门店营业额的平均值在$$[ 2 0， 2 5 ]$$内
C.根据乙门店的营业额折线图可知，其营业额总体是上升趋势
D.乙门店在这$${{9}}$$个月份中的营业额的极差为$${{2}{5}}$$万元
第一题解析：
首先计算A、B两家企业的各项统计指标：
对于A企业：
极差 = 98 - 43 = 55
中位数 = (75 + 78)/2 = 76.5
平均数 = (43+72+73+98+63+86+65+75+81+78)/10 = 73.4
众数：无重复值，无众数
对于B企业：
极差 = 94 - 37 = 57
中位数 = (68 + 68)/2 = 68
平均数 = (82+68+71+37+61+65+58+68+77+94)/10 = 68.1
众数：68（出现2次）
选项分析：
A. A企业极差55小于B企业极差57，错误
B. A企业中位数76.5大于B企业中位数68，错误
C. A企业平均数73.4大于B企业平均数68.1，错误
D. B企业众数与中位数都是68，正确
正确答案：D
第二题解析：
计算各选项：
A. 甲平均分=(10+10+10+20+0)/5=10，丙平均分=(10+10+15+15+10)/5=12，错误
B. 乙极差=15-5=10，丁极差=20-0=20，错误
C. 平均数不能推断个体情况，错误
D. 第3题得分：10,5,15,10，方差=[(10-10)²+(5-10)²+(15-10)²+(10-10)²]/4=12.5
第5题得分：0,10,10,20，方差=[(0-10)²+(10-10)²+(10-10)²+(20-10)²]/4=50
12.5 < 50，正确
正确答案：D
第三题解析：
判断是否进入决赛需要知道前8名的成绩分界线，即第8名的成绩（第8小的成绩）。这对应于15名同学成绩的中位数（第8名的成绩）。
平均数只能反映整体水平，极差只能反映波动范围，都不能确定具体排名。
正确答案：C
第四题解析：
数据排序：14,18,20,20,21,22,23,25,26
①极差=26-14=12，正确
②中位数=21（第5个数），正确
③平均数=(14+18+20+20+21+22+23+25+26)/9=189/9=21，正确
④方差计算：
各数与平均数的差：-7,-3,-1,-1,0,1,2,4,5
平方和=49+9+1+1+0+1+4+16+25=106
方差=106/9≈11.78，题目给出11，不精确但最接近
正确答案：D（4个说法都基本正确）
第五题解析：
根据控制标准"连续7天每天新增≤5人"：
①平均数≤3，可能有某天>5（如7,0,0,0,0,0,0），不符合
②平均数≤3且s≤2，限制波动，但仍有可能性（如4,4,4,3,2,2,2），不符合
③平均数≤3且极差≤2，最大值≤平均数+极差/2≈4≤5，符合
④众数=1且极差≤4，最大值≤5（如1,1,1,1,5,1,1），符合
正确答案：C（③④）