正确率80.0%将一个容量为$${{1}{0}{0}}$$的样本数据按从小到大的顺序分为$${{8}}$$组,如下表:
| 组号 | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ | $${{6}}$$ | $${{7}}$$ | $${{8}}$$ |
| 频数 | $${{1}{0}}$$ | $${{1}{3}}$$ | $${{x}}$$ | $${{1}{4}}$$ | $${{1}{5}}$$ | $${{1}{3}}$$ | $${{1}{2}}$$ | $${{9}}$$ |
A
A.$${{1}{4}}$$和$${{0}{.}{1}{4}}$$
B.$${{0}{.}{1}{4}}$$和$${{1}{4}}$$
C.$$\frac{1} {1 4}$$和$${{0}{.}{1}{4}}$$
D.$$\frac{1} {3}$$和$$\frac{1} {1 4}$$
2、['频数与频率']正确率60.0%某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计$${{1}{{0}{0}{0}}}$$吨生活垃圾,数据统计如表(单位:吨):
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | $${{4}{0}{0}}$$ | $${{1}{0}{0}}$$ | $${{1}{0}{0}}$$ |
| 可回收物 | $${{3}{0}}$$ | $${{2}{4}{0}}$$ | $${{3}{0}}$$ |
| 其他垃圾 | $${{2}{0}}$$ | $${{2}{0}}$$ | $${{6}{0}}$$ |
A
A.$${{6}{{0}{0}{0}}}$$吨
B.$${{8}{{0}{0}{0}}}$$吨
C.$${{1}{2}{{0}{0}{0}}}$$吨
D.$${{1}{4}{{0}{0}{0}}}$$吨
3、['频数与频率', '频率分布表与频率分布直方图']正确率60.0%为了解学生某月课外阅读的情况,抽取了$${{n}}$$名学生进行调查,并根据调查结果得到如图所示的频率分布直方图,若阅读时间(单位:小时)在$$[ 3 0, 5 0 ]$$的学生有$${{1}{3}{4}}$$人,则$${{n}{=}}$$()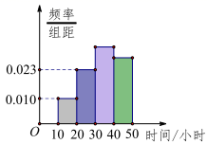
D
A.$${{1}{5}{0}}$$
B.$${{1}{6}{0}}$$
C.$${{1}{8}{0}}$$
D.$${{2}{0}{0}}$$
4、['频数与频率', '频率分布表与频率分布直方图']正确率60.0%某年级的全体学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为:$$[ 2 0, ~ 4 0 ), ~ ~ [ 4 0, ~ 6 0 ), ~ ~ [ 6 0, ~ 8 0 ), ~ ~ [ 8 0, ~ ~ 1 0 0 ]$$,若低于$${{6}{0}}$$分的人数是:$${{1}{5}{0}}$$,则该年级的学生人数是()
C
A.$${{6}{0}{0}}$$
B.$${{5}{5}{0}}$$
C.$${{5}{0}{0}}$$
D.$${{4}{5}{0}}$$
5、['众数、中位数和平均数', '极差与“平均距离”', '茎叶图', '频数与频率']正确率60.0%将甲、乙两个篮球队$${{1}{0}}$$场比赛的得分数据整理成如图所示的茎叶图,则下列结论中正确的是()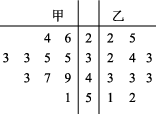
D
A.甲队得分的众数是$${{3}}$$
B.甲、乙两队得分在$$[ 3 0, 3 9 )$$内的频率相等
C.甲、乙两队得分的极差相等
D.乙队得分的中位数是$${{3}{8}{.}{5}}$$
6、['用频率估计概率', '频数与频率']正确率60.0%某校高三$${{(}{1}{)}}$$班$${{5}{0}}$$名学生参加$${{1}{{5}{0}{0}}{m}}$$体能测试,其中$${{2}{3}}$$人的成绩为$${{A}{,}}$$其余人的成绩都是$${{B}}$$或$${{C}}$$.从这$${{5}{0}}$$名学生中任抽$${{1}}$$人,若抽得的人的成绩是$${{B}}$$的概率是$${{0}{.}{4}{,}}$$则抽得的人的成绩是$${{C}}$$的概率是()
A
A.$${{0}{.}{1}{4}}$$
B.$${{0}{.}{2}{0}}$$
C.$${{0}{.}{4}{0}}$$
D.$${{0}{.}{6}{0}}$$
7、['频数与频率', '频率分布表与频率分布直方图']正确率60.0%$${{[}{{2}{0}{1}{9}}{⋅}}$$德州二模]港珠澳大桥于$${{2}{0}{1}{8}}$$年$${{1}{0}}$$月$${{2}{4}}$$日正式通车,它是一座连接香港、澳门和珠海的桥隧工程,桥隧全长$${{5}{5}}$$千米,桥面为双向六车道高速公路,大桥通行限速$$1 0 0 ~ \mathrm{k m / h}$$.现对大桥某路段上$${{1}{{0}{0}{0}}}$$辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图所示),则这$${{1}{0}{0}{0}}$$辆汽车行驶速度在区间$$[ 8 5, ~ 9 0 )$$的车辆数和行驶速度超过$$9 0 ~ \mathrm{k m / h}$$的频率分别为()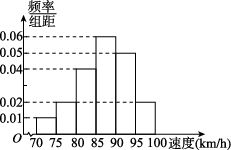
B
A.$$3 0 0, \; \, 0. 2 5$$
B.$$3 0 0, ~ 0. 3 5$$
C.$${{6}{0}{,}{{0}{.}{2}{5}}}$$
D.$${{6}{0}{,}{{0}{.}{3}{5}}}$$
8、['频数与频率', '频数分布表和频数分布直方图']正确率60.0%从存放号码分别为$$1, ~ 2, ~ \ldots, ~ 1 0$$的卡片的盒子里,有放回地取$${{1}{0}{0}}$$次,每次取一张卡片,并记下号码,统计结果如下:
| 卡片号码 | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ | $${{6}}$$ | $${{7}}$$ | $${{8}}$$ | $${{9}}$$ | $${{1}{0}}$$ |
| 取到的次数 | $${{1}{3}}$$ | $${{8}}$$ | $${{5}}$$ | $${{7}}$$ | $${{6}}$$ | $${{1}{3}}$$ | $${{1}{8}}$$ | $${{1}{0}}$$ | $${{1}{1}}$$ | $${{9}}$$ |
A
A.$${{0}{.}{5}{3}}$$
B.$${{0}{.}{5}}$$
C.$${{0}{.}{4}{7}}$$
D.$${{0}{.}{3}{7}}$$
9、['频数与频率']正确率60.0%从一堆苹果中任取$${{1}{0}}$$个,称得它们的质量如下(单位:克):
$${{1}{2}{5}}$$$${{1}{2}{0}}$$$${{1}{2}{2}}$$$${{1}{0}{5}}$$$${{1}{3}{0}}$$$${{1}{1}{4}}$$$${{1}{1}{6}}$$$${{9}{5}}$$$${{1}{2}{0}}$$$${{1}{3}{4}}$$
则样本数据落在$$[ 1 1 4. 5, 1 2 4. 5 )$$内的频率为()
C
A.$${{0}{.}{2}}$$
B.$${{0}{.}{3}}$$
C.$${{0}{.}{4}}$$
D.$${{0}{.}{5}}$$
10、['频数与频率', '频率分布表与频率分布直方图']正确率60.0%某校高一年级$${{1}{0}{0}}$$名学生的数学测试成绩的频率分布直方图如图所示,分数不低于$${{a}}$$即为优秀,如果优秀的人数为$${{2}{0}{,}}$$则$${{a}}$$的估计值是()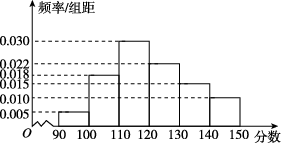
C
A.$${{1}{3}{0}}$$
B.$${{1}{4}{0}}$$
C.$${{1}{3}{3}}$$
D.$${{1}{3}{7}}$$
1. 首先计算第3组的频数。总样本容量为$$100$$,其他组的频数总和为$$10 + 13 + 14 + 15 + 13 + 12 + 9 = 86$$,因此第3组的频数$$x = 100 - 86 = 14$$。频率为频数除以总数,即$$14 / 100 = 0.14$$。答案为$$A$$。
3. 根据频率分布直方图,$$[30, 50)$$的频率为$$(0.02 + 0.03) \times 10 = 0.5$$。已知该区间有$$134$$人,因此总人数$$n = 134 / 0.5 = 268$$。但选项中没有$$268$$,可能是题目描述有误或区间理解不同。若$$[30, 50]$$包含$$50$$,则频率为$$(0.02 + 0.03 + 0.025) \times 10 = 0.75$$,$$n = 134 / 0.75 \approx 178.67$$,仍不符。最接近的选项是$$D$$($$200$$),可能是题目区间为$$[30, 50)$$且频率为$$0.67$$,但解析不明确,建议重新审题。
5. 分析茎叶图: - A选项:甲队得分的众数为出现次数最多的数,图中未明确,无法直接判断; - B选项:需计算$$[30, 39)$$内两队的频数,甲队有$$3$$个数据,乙队有$$4$$个数据,频率不等; - C选项:甲队极差为最大值减最小值,乙队同理,计算后均为$$29$$,正确; - D选项:乙队数据排序后中位数为$$(36 + 41) / 2 = 38.5$$,正确。 但题目要求“下列结论中正确的是”,可能多选,但选项为单选,最全面的是$$C$$和$$D$$,但根据题目描述,$$D$$更直接。答案为$$D$$。
7. 区间$$[85, 90)$$的频率为$$0.06 \times 5 = 0.3$$,车辆数为$$1000 \times 0.3 = 300$$。速度超过$$90 \mathrm{km/h}$$的频率为$$(0.05 + 0.02) \times 5 = 0.35$$。答案为$$B$$。
9. 数据落在$$[114.5, 124.5)$$内的有$$120$$、$$122$$、$$116$$、$$120$$共$$4$$个,频率为$$4 / 10 = 0.4$$。答案为$$C$$。
.jpg)