.jpg)
正确率60.0%如图所示的茎叶图(茎是十位上的数字，叶是个数上的数字)的中位数是$${{m}}$$，若双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 \， ( a > 0， b > 0 )$$的一条渐近线方程为$$y=-\frac{2 m} {1 7} x$$，该双曲线的离心率是（）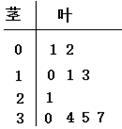
C
A.$$\frac{\sqrt5} {2}$$
B.$${\sqrt {3}}$$
C.$${\sqrt {5}}$$
D.$${{2}{\sqrt {3}}}$$
2、['方差与标准差'， '众数、中位数和平均数'， '茎叶图']正确率60.0%已知$${{A}{，}{B}}$$两家酒店的综合评分如图所示，记$${{A}{，}{B}}$$两家酒店的综合评分的平均数分别为$$\bar{x}_{A}， ~ \bar{x}_{B}，$$方差分别为$$s_{A}^{2}， \ s_{B}^{2}，$$则（）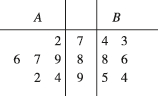
B
A.$$\bar{x}_{A} > \bar{x}_{B}， \; \; s_{A}^{2} > s_{B}^{2}$$
B.$$\bar{x}_{A} > \bar{x}_{B}， \; \; s_{A}^{2} < \; s_{B}^{2}$$
C.$$\bar{x}_{A} < \bar{x}_{B}， \ s_{A}^{2} > s_{B}^{2}$$
D.$$\bar{x}_{A} < \bar{x}_{B}， \ s_{A}^{2} < \ s_{B}^{2}$$
3、['众数、中位数和平均数'， '茎叶图']正确率80.0%如图所示的茎叶图记录了甲、乙两组各$${{5}}$$名工人某日的产量数据$${{(}}$$单位：件$${{)}{.}}$$若这两组数据的中位数相等，且平均值也相等，则$${{x}}$$和$${{y}}$$的值分别为（）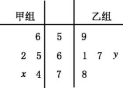
A
A.$${{3}{，}{5}}$$
B.$${{5}{，}{5}}$$
C.$${{3}{，}{7}}$$
D.$${{5}{，}}$$$${{7}}$$
4、['众数、中位数和平均数'， '茎叶图']正确率80.0%
如图所示的茎叶图记录了甲、乙两名员工连续$${{5}}$$天内的日产量数据$${{(}}$$单位：箱$${{)}{.}}$$已知这两组数据的平均数分别为
，
，若这两组数据的中位数相等，则$${{(}{)}}$$
A.
B.$$\overline{{x}}_{\pi}=\overline{{x}}_{\mathrm{Z}}$$
C.
D.，的大小关系不确定
正确率60.0%为比较甲、乙两地某月$${{1}{4}}$$时的气温，随机选取该月中的$${{5}}$$天，将这$${{5}}$$天中$${{1}{4}}$$时的气温数据(单位：$${^{∘}{C}{)}}$$制成如图所示的茎叶图，现有以下结论：①甲地该月$${{1}{4}}$$时的平均气温低于乙地该月$${{1}{4}}$$时的平均气温；②甲地该月$${{1}{4}}$$时的平均气温高于乙地该月$${{1}{4}}$$时的平均气温；③甲地该月$${{1}{4}}$$时气温的中位数小于乙地该月$${{1}{4}}$$时气温的中位数；④甲地该月$${{1}{4}}$$时气温的中位数大于乙地该月$${{1}{4}}$$时气温的中位数.若茎叶图中的数据很好地代表了两地的气温，则正确结论的编号为（）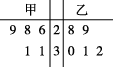
A
A.①③
B.①④
C.②③
D.②④
6、['茎叶图']正确率60.0%下图是甲$${、}$$乙两人六次综合测评成绩的茎叶图，其中一个数字被污损，若$${{x}{∈}{{N}^{∗}}}$$且$${{x}{<}{{1}{0}}}$$，则甲的中位数超过乙的中位数的概率为（）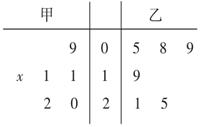
B
A.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
C.$$\frac{1} {3}$$
D.$$\begin{array} {l l} {\frac{4} {9}} \\ \end{array}$$
7、['茎叶图'， '算法与程序框图']正确率60.0%如图$${{1}}$$是某学习小组学生在某次数学考试中成绩的茎叶图，$${{1}}$$号到$${{2}{0}}$$号同学的成绩依次为$$a_{1}， a_{2}， a_{3}， \cdots\cdots a_{2 0}$$，图$${{2}}$$是统计茎叶图中成绩在一定范围内的学生人数的程序框图，那么该框图的输出结果是（）
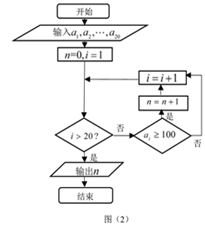
B
A.$${{1}{2}}$$
B.$${{8}}$$
C.$${{9}}$$
D.$${{1}{1}}$$
8、['众数、中位数和平均数'， '茎叶图']正确率60.0%如图所示的茎叶图记录了甲、乙两组各$${{5}}$$名工人某日加工某产品的产量数据(单位：件)，若这两组数据的中位数相等，且平均值也相等，则$${{x}}$$和$${{y}}$$的值分别为（）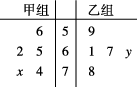
B
A.$${{5}}$$，$${{5}}$$
B.$${{3}}$$，$${{5}}$$
C.$${{3}}$$，$${{7}}$$
D.$${{5}}$$，$${{7}}$$
9、['众数、中位数和平均数'， '茎叶图']正确率60.0%某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，随机选取了$${{4}{0}}$$名工人，将他们随机分成两组，每组$${{2}{0}}$$人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间(单位：分钟)绘制了如图所示的茎叶图，则下列结论中不正确的是（）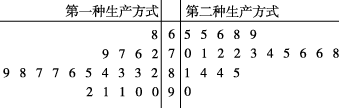
D
A.用第一种生产方式的工人中，有$${{7}{5}{%}}$$的工人完成生产任务所需要的时间不少于$${{8}{0}}$$分钟
B.第二种生产方式比第一种生产方式的效率更高
C.这$${{4}{0}}$$名工人完成任务所需时间的中位数为$${{8}{0}}$$分钟
D.无论用哪种生产方式的工人完成生产任务所需要的平均时间都是$${{8}{0}}$$分钟
10、['众数、中位数和平均数'， '极差与“平均距离”'， '茎叶图']正确率60.0%某学生在一门功课的$${{2}{2}}$$次考试中，所得分数的茎叶图如图所示，则此学生该门功课考试成绩的极差与中位数之和为（）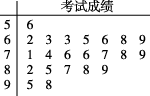
B
A.$${{1}{1}{7}}$$
B.$${{1}{1}{8}}$$
C.$$1 1 8. 5$$
D.$$1 1 9. 5$$
1. 首先从茎叶图中提取数据并排序，计算中位数$$m$$。然后根据双曲线的渐近线方程$$y=-\frac{2m}{17}x$$，结合双曲线的性质$$\frac{b}{a}=\frac{2m}{17}$$，再利用离心率公式$$e=\sqrt{1+\frac{b^2}{a^2}}$$计算即可。
3. 分别列出甲、乙两组工人的产量数据，根据中位数相等和平均值相等的条件建立方程，解出$$x$$和$$y$$的值。
5. 从茎叶图中提取甲、乙两地的气温数据，分别计算平均气温和中位数，比较后判断结论的正确性。
7. 分析程序框图的逻辑，统计茎叶图中成绩在指定范围内的学生人数。根据茎叶图的数据和程序框图的判断条件，得出输出结果。
9. 分析茎叶图中两种生产方式的工作时间数据，计算中位数、平均时间以及完成时间的比例，判断结论的正确性。