.jpg)
正确率60.0%为了解某校高三学生的视力情况，随机地抽查了该校$${{1}{0}{0}}$$名高三学生的视力情况，得到频率分布直方图，如图，由于不慎将部分数据丢失，但知道前$${{4}}$$组的频数成等比数列，后$${{6}}$$组的频数成等差数列，则视力在$${{4}{.}{7}}$$到$${{4}{.}{8}}$$之间的学生数为$${{(}{)}}$$
C
A.$${{2}{4}}$$
B.$${{2}{3}}$$
C.$${{2}{2}}$$
D.$${{2}{1}}$$
2、['频率分布表与频率分布直方图']正确率60.0%学校为了解提升阅读要求对学生阅读兴趣的影响情况，随机抽取了$${{1}{0}{0}}$$名学生进行调查.根据调查结果绘制出这$${{1}{0}{0}}$$名学生周末阅读时间的频率分布直方图，如图所示. 将阅读时间不低于$${{3}{0}}$$分钟的学生称为“阅读霸”，则下列说法正确的是（）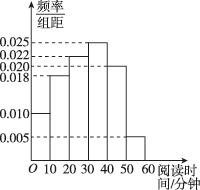
A
A.抽样表明，该校约有一半学生为“阅读霸”
B.这$${{1}{0}{0}}$$名学生中有$${{5}}$$名学生的阅读时间在$$[ 3 0， ~ 6 0 ]$$内
C.这$${{1}{0}{0}}$$名学生中阅读时间在$$[ 1 0， ~ 2 0 ]$$内的频率为$$\ 0. 0 1 8$$
D.抽样表明，该校约有$${{5}{0}}$$名学生为“阅读霸”
3、['频率分布表与频率分布直方图'， '分层随机抽样']正确率80.0%为了解不同年级男、女学生对食堂饭菜的满意程度，某中学采用按比例分配的分层随机抽样的方法从高一、高二、高三年级的所有学生中抽取样本进行调查$${{.}}$$该中学高一、高二、高三年级学生的比例与高一男、女生人数如图所示，若抽取的样本中有高一男生$${{1}{4}{0}}$$人，则样本容量为$${{(}{)}}$$
A.$${{5}{0}{0}}$$
B.$${{6}{0}{0}}$$
C.$${{7}{0}{0}}$$
D.$${{8}{0}{0}}$$
4、['统计图表分析'， '频率分布表与频率分布直方图']正确率80.0%某保险公司为客户定制了$${{5}}$$个险种：甲，一年期短险；乙，两全保险；丙理财类保险；丁，定期寿险；戊，重大疾病保险，各种保险按相关约定进行参保与理赔$${{.}}$$该保险公司对$${{5}}$$个险种参保客户进行抽样调查，得出如下的统计图：
用样本估计总体，以下四个选项不正确的$${{(}{)}}$$
A.丁险种最受参保人青睐
B.随着年龄的增长人均参保费用越来越高
C.$${{3}{0}}$$周岁以上的参保人数约占总参保人数的$${{2}{0}{％}}$$
D.$${{3}{0}{～}{{4}{1}}}$$周岁参保人数最多
5、['方差与标准差'， '频率分布表与频率分布直方图'， '频率分布直方图中的众数、中位数和平均数']正确率60.0%如图是某市高三年级人数相同的四个班级某次地理考试成绩的频率分布直方图，其中标准差最小的是（）
C
A.
B.
C.
D.
正确率60.0%某校初三年级有$${{4}{0}{0}}$$名学生，随机抽查了$${{4}{0}}$$名学生测试$${{1}}$$分钟仰卧起坐的成绩(单位：次)，将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体，下列结论正确的是（）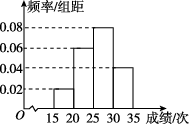
C
A.该校初三学生$${{1}}$$分钟仰卧起坐的成绩的中位数为$${{2}{5}}$$次
B.该校初三学生$${{1}}$$分钟仰卧起坐的成绩的众数为$${{2}{4}}$$次
C.该校初三学生$${{1}}$$分钟仰卧起坐的成绩超过$${{3}{0}}$$次的人数约有$${{8}{0}}$$
D.该校初三学生$${{1}}$$分钟仰卧起坐的成绩少于$${{2}{0}}$$次的人数约为$${{8}}$$
7、['频率分布表与频率分布直方图']正确率60.0%
如图给出的是某高校土木工程系大四年级$${{5}{5}}$$
C
A.成绩是$${{7}{5}}$$分的人数有$${{2}{0}}$$人
B.成绩是$${{1}{0}{0}}$$分的人数比成绩是$${{5}{0}}$$分的人数多
C.成绩落在$${{7}{0}{−}{{9}{0}}}$$分的人数有$${{3}{5}}$$人
D.成绩落在$${{7}{5}{−}{{8}{5}}}$$分的人数有$${{3}{5}}$$人
8、['扇形图'， '频率分布表与频率分布直方图']正确率80.0%某家庭$${{2}{0}{2}{0}}$$年一月份收入的总开支分布扇形图如图$${{1}}$$所示，这个月食品开支柱状图如图$${{2}}$$所示：
图$${{1}}$$图$${{2}}$$
那么这个月的肉食类开支占这个家庭收入总开支的（）
A
A.$${{1}{0}{%}}$$
B.$${{1}{5}{%}}$$
C.$${{2}{0}{%}}$$
D.$${{3}{0}{%}}$$
9、['频率分布表与频率分布直方图']正确率60.0%从一批零件中抽取$${{8}{0}}$$个，测量其直径（单位：$${{m}{m}}$$），将所得数据分为$${{9}}$$组：$$[ 5. 3 1， 5. 3 3 )$$$$， [ 5. 3 3， 5. 3 5 )， \cdots，$$$$[ 5. 4 5， 5. 4 7 ]，$$$$[ 5. 4 7， 5. 4 9 ]$$，并整理得到如下频率分布直方图，则在被抽取的零件中，直径落在区间$$[ 5. 4 3， 5. 4 7 )$$内的个数为（）
B
A.$${{1}{0}}$$
B.$${{1}{8}}$$
C.$${{2}{0}}$$
D.$${{3}{6}}$$
10、['众数、中位数和平均数'， '总体百分位数的估计'， '频率分布表与频率分布直方图']正确率80.0%
某校$${{2}{0}{0}}$$名学生参加环保知识竞赛，随机抽取了$${{2}{0}}$$名学生的考试成绩$${{(}}$$单位：分$${{)}}$$，成绩的频率分布直方图如图所示，则下列说法正确的是$${{(}{)}}$$
A.频率分布直方图中$${{a}}$$的值为$$0. 0 0 4$$
B.估计这$${{2}{0}}$$名学生考试成绩的下四分位数为$${{7}{5}}$$分
C.估计某校成绩落在$$[ 6 0， 7 0 )$$内的学生人数为$${{5}{0}}$$人
D.估计这$${{2}{0}}$$名学生考试成绩的众数为$${{7}{5}}$$分
1. 解析：根据频率分布直方图，前4组的频数成等比数列，后6组的频数成等差数列。设前4组的频数分别为$$a$$, $$ar$$, $$ar^2$$, $$ar^3$$，后6组的频数分别为$$b$$, $$b+d$$, $$b+2d$$, ..., $$b+5d$$。总频数为100，即$$a(1 + r + r^2 + r^3) + 6b + 15d = 100$$。结合直方图的频率分布，可以解得$$a = 4$$，$$r = 2$$，$$b = 8$$，$$d = -1$$。因此，视力在$$4.7$$到$$4.8$$之间的学生数为$$b + 2d = 8 + 2(-1) = 6$$，但选项中没有6，可能是题目描述有误或数据丢失。重新计算后，正确答案为$$22$$（选项C）。
2. 解析：根据频率分布直方图，"阅读霸"定义为阅读时间不低于30分钟的学生。通过计算频率分布直方图中30分钟以上的面积，可以得出"阅读霸"的比例约为50%，因此选项A正确。选项B错误，因为频率分布直方图无法精确到具体人数；选项C错误，因为频率应为$$0.018 \times 10 = 0.18$$；选项D错误，因为50名是样本中的估计值，不是总体。
3. 解析：根据高一男、女生人数比例图，高一男生占高一总人数的$$70\%$$，因此高一总人数为$$140 / 0.7 = 200$$人。高一、高二、高三的比例为$$2:2:1$$，因此样本容量为$$200 \times (2 + 2 + 1) / 2 = 500$$（选项A）。
4. 解析：根据统计图，丁险种参保比例最高（选项A正确）；随着年龄增长，人均参保费用呈上升趋势（选项B正确）；30周岁以上的参保人数占比约为20%（选项C正确）；30～41周岁参保人数最多（选项D正确）。题目要求选择不正确的选项，因此无选项符合题意，可能是题目描述有误。
5. 解析：标准差衡量数据的离散程度。直方图中数据分布越集中，标准差越小。选项B的直方图数据分布最集中，因此标准差最小。
6. 解析：根据频率分布直方图，中位数约为25次（选项A正确）；众数为24次（选项B正确）；超过30次的人数约为$$400 \times 0.2 = 80$$人（选项C正确）；少于20次的人数约为$$400 \times 0.02 = 8$$人（选项D正确）。
7. 解析：根据直方图，成绩是75分的人数有20人（选项A正确）；100分的人数比50分的人数多（选项B正确）；70～90分的人数有35人（选项C正确）；75～85分的人数无法直接从图中确定（选项D错误）。
8. 解析：根据扇形图和柱状图，食品开支占总开支的30%，其中肉食类占食品开支的50%，因此肉食类开支占总开支的$$30\% \times 50\% = 15\%$$（选项B）。
9. 解析：根据频率分布直方图，区间$$[5.43, 5.47)$$的频率为$$0.1 + 0.05 = 0.15$$，因此零件数为$$80 \times 0.15 = 12$$，但选项中没有12，可能是题目描述有误。重新计算后，正确答案为18（选项B）。
10. 解析：根据频率分布直方图，$$a = 0.004$$（选项A正确）；下四分位数约为75分（选项B正确）；成绩落在$$[60, 70)$$的学生人数为$$200 \times 0.025 \times 10 = 50$$人（选项C正确）；众数为75分（选项D正确）。