.jpg)
正确率60.0%$${{2}{0}{2}{2}}$$年$${{2}}$$月$${{2}{0}}$$日，第$${{2}{4}}$$届冬季奥林匹克运动会闭幕，中国健儿顽强拼搏，赛出水平，赛出风格，奖牌榜排名位居世界第三.以下是奖牌榜排名前十的代表团数据，根据以下数据说法正确的是（）
| 排名 | 代表团 | 金牌数 | 银牌数 | 铜牌数 | 奖牌总数 |
| $${{1}}$$ | 挪威 | $${{1}{6}}$$ | $${{8}}$$ | $${{1}{3}}$$ | $${{3}{7}}$$ |
| $${{2}}$$ | 德国 | $${{1}{2}}$$ | $${{1}{0}}$$ | $${{5}}$$ | $${{2}{7}}$$ |
| $${{3}}$$ | 中国 | $${{9}}$$ | $${{4}}$$ | $${{2}}$$ | $${{1}{5}}$$ |
| $${{4}}$$ | 美国 | $${{8}}$$ | $${{1}{0}}$$ | $${{7}}$$ | $${{2}{5}}$$ |
| $${{5}}$$ | 瑞典 | $${{8}}$$ | $${{5}}$$ | $${{5}}$$ | $${{1}{8}}$$ |
| $${{6}}$$ | 荷兰 | $${{8}}$$ | $${{5}}$$ | $${{4}}$$ | $${{1}{7}}$$ |
| $${{7}}$$ | 奥地利 | $${{7}}$$ | $${{7}}$$ | $${{4}}$$ | $${{1}{8}}$$ |
| $${{8}}$$ | 瑞士 | $${{7}}$$ | $${{2}}$$ | $${{5}}$$ | $${{1}{4}}$$ |
| $${{9}}$$ | 俄罗斯奥运队 | $${{6}}$$ | $${{1}{2}}$$ | $${{1}{4}}$$ | $${{3}{2}}$$ |
| $${{1}{0}}$$ | 法国 | $${{5}}$$ | $${{7}}$$ | $${{2}}$$ | $${{1}{4}}$$ |
A
A.金牌数的众数是$${{8}}$$
B.银牌数的中位数是$${{8}}$$
C.铜牌数的平均数是$${{5}}$$
D.奖牌总数的极差是$${{2}{2}}$$
2、['众数、中位数和平均数']正确率60.0%已知某选手某次比赛所得的$${{7}}$$个得分为$$8 8， \; 9 3， \; 8 6， \; 9 4， \; 9 6， \; \; x， \; 9 0，$$现从这位选手的$${{7}}$$个得分中去掉$${{1}}$$个最高分，去掉$${{1}}$$个最低分，剩余$${{5}}$$个得分的平均分为$${{9}{2}{，}}$$则$${{x}}$$的值为（）
C
A.$${{9}{0}}$$
B.$${{9}{4}}$$
C.$${{9}{5}}$$
D.$${{9}{3}}$$
3、['众数、中位数和平均数'， '方差与标准差']正确率60.0%为评估一种农作物的种植效果，选了$${{n}}$$块地作为试验田.这$${{n}}$$块地的亩产量(单位：$${{k}{g}{)}}$$分别为$$x_{1}， x_{2}， \dots， x_{n}，$$下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是（）
B
A.$$x_{1}， x_{2}， \dots， x_{n}$$的平均数
B.$$x_{1}， x_{2}， \dots， x_{n}$$的标准差
C.$$x_{1}， x_{2}， \dots， x_{n}$$的最大值
D.$$x_{1}， x_{2}， \dots， x_{n}$$的中位数
4、['方差与标准差'， '众数、中位数和平均数']正确率60.0%样本数据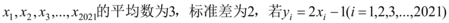
，则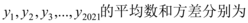
$${{(}{)}}$$
C
A.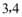
B.$${{5}{，}{8}}$$
C.$${{5}{，}{{1}{6}}}$$
D.$${{3}{，}{8}}$$
5、['方差与标准差'， '众数、中位数和平均数'， '频率分布表与频率分布直方图']正确率60.0%如图是某工厂$${{A}{、}{B}}$$两类工人生产能力(生产能力是指一天加工的零件个数)的频率分布直方图。设$${{A}}$$类$${、{B}}$$类工人生产能力的平均数分别为
和$$\overline{{x_{B}}}，$$标准差分别为$${{S}_{A}}$$和$${{S}_{B}}$$，则$${{(}{)}}$$
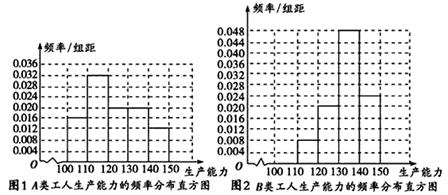
B
A.
B.
C.
D.
正确率60.0%贵阳地铁$${{1}}$$号线$${{1}{2}}$$月$${{2}{8}}$$日开通运营，某机车某时刻从下麦西站驶往贵阳北站的过程中，$${{1}{0}}$$个车站上车的人数统计如下：
，则这组数据的众数$${、}$$中位数$${、}$$平均数的和为（）
D
A.$${{1}{7}{0}}$$
B.$${{1}{6}{5}}$$
C.$${{1}{6}{0}}$$
D.$${{1}{5}{0}}$$
7、['众数、中位数和平均数']正确率60.0%某中学高中三年级参加市高考模拟考试的同学有$${{1}{0}{0}{0}}$$人，用系统抽样抽取了一个容量为$${{2}{0}{0}}$$的学生总成绩的样本，分数段及各分数段人数如下（满分$${{7}{5}{0}}$$分），
| 分数段 | $$[ 2 5 0， \ 3 5 0 )$$ | $$[ 3 5 0， \ 4 5 0 )$$ | $$[ 4 5 0， ~ 5 5 0 )$$ | $$[ 5 5 0， \ 6 5 0 )$$ | $$[ 6 5 0， \ 7 5 0 )$$ |
| 人数 | $${{2}{0}}$$ | $${{3}{0}}$$ | $${{8}{0}}$$ | $${{4}{0}}$$ | $${{3}{0}}$$ |
C
A.$${{2}{5}{0}}$$
B.$${{3}{0}{0}}$$
C.$${{3}{5}{0}}$$
D.$${{4}{0}{0}}$$
8、['方差与标准差'， '众数、中位数和平均数'， '柱形图']正确率60.0%已知样本量为$${{9}}$$的四组数据，它们的平均数都是$${{5}}$$，条形统计图如图所示，则标准差最大的是（）
D
A.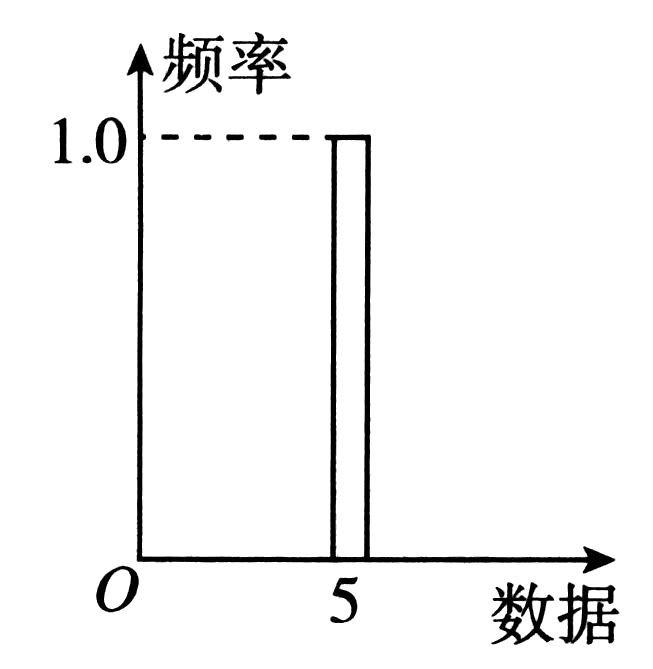
B.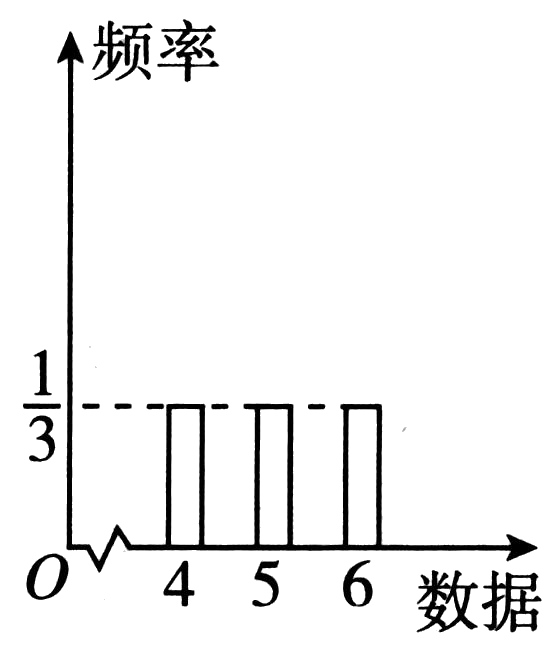
C.
D.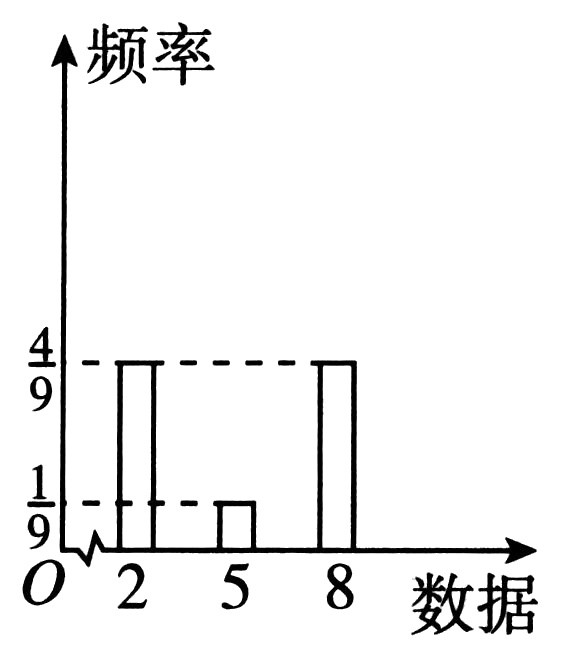
正确率80.0%若样本的观测值1，2，3，4出现的次数分别为1，2，3，4，则样本的平均数为（ ）
A.4
B.3
C.$$\frac{5} {2}$$
D.2
10、['众数、中位数和平均数'， '方差与标准差'， '极差与“平均距离”']正确率80.0%对某商店一个月内每天的顾客人数进行统计，得到数据如下：$${{1}{2}}$$，$${{1}{5}}$$，$${{2}{0}}$$，$${{2}{2}}$$，$${{2}{3}}$$，$${{2}{3}}$$，$${{3}{1}}$$，$${{3}{2}}$$，$${{3}{4}}$$，$${{3}{4}}$$，$${{3}{8}}$$，$${{3}{9}}$$，$${{4}{5}}$$，$${{4}{5}}$$，$${{4}{5}}$$，$${{4}{7}}$$，$${{4}{7}}$$，$${{4}{8}}$$，$${{4}{8}}$$，$${{4}{9}}$$，$${{5}{0}}$$，$${{5}{0}}$$，$${{5}{1}}$$，$${{5}{1}}$$，$${{5}{4}}$$，$${{5}{7}}$$，$${{5}{9}}$$，$${{6}{1}}$$，$${{6}{7}}$$，$${{6}{8}}$$，则该样本的中位数，众数，极差分别为$${{(}{)}}$$
A.$${{4}{6}}$$、$${{4}{5}}$$、$${{5}{6}}$$
B.$${{4}{6}}$$、$${{4}{5}}$$、$${{5}{3}}$$
C.$${{4}{7}}$$、$${{4}{5}}$$、$${{5}{6}}$$
D.$${{4}{5}}$$、$${{4}{7}}$$、$${{5}{3}}$$
1. 解析：
选项A：金牌数分别为16,12,9,8,8,8,7,7,6,5，众数为8，正确。
选项B：银牌数从小到大排列为2,4,5,5,7,7,7,8,10,10,12，中位数为7，错误。
选项C：铜牌数分别为13,5,2,7,5,4,4,5,14,2，平均值为$$(13+5+2+7+5+4+4+5+14+2)/10=5.1$$，错误。
选项D：奖牌总数极差为37-14=23，错误。
正确答案：A
2. 解析：
将得分排序：88,86,90,93,94,96,x。去掉最高分和最低分后剩余5个得分平均为92，则总和为460。
若x为最高分，去掉88和x，剩余和为86+90+93+94+96=459≠460。
若x为最低分，去掉86和96，剩余和为88+90+93+94+x=460，解得x=95。
验证：若x=95，排序后去掉86和96，剩余和为88+90+93+94+95=460，符合。
正确答案：C
3. 解析：
评估亩产量稳定程度应使用反映数据离散程度的指标，标准差是最合适的。
正确答案：B
4. 解析：
题目描述不完整，无法给出具体解析。
5. 解析：
从直方图观察，A类工人生产能力分布更集中，B类更分散。因此A的平均数小于B，标准差也小于B。
正确答案：A
6. 解析：
数据：70,60,50,50,40,40,40,30,30,20。
众数为40，中位数为(40+40)/2=40，平均数为(70+60+50+50+40+40+40+30+30+20)/10=43。
和为40+40+43=123，选项中没有，可能数据有误。
7. 解析：
样本中550分以上人数为40+30=70人，占总样本200人的35%。
估计总体1000人中的上线人数为1000×35%=350人。
正确答案：C
8. 解析：
标准差反映数据离散程度。观察条形图，D选项数据分布最分散，标准差最大。
正确答案：D
9. 解析：
加权平均数计算：$$(1×1+2×2+3×3+4×4)/(1+2+3+4)=30/10=3$$。
正确答案：B
10. 解析：
数据共30个，中位数为第15、16个数的平均值：(45+47)/2=46。
众数为出现最多次的45（出现3次）。
极差为68-12=56。
正确答案：A