正确率60.0%已知等差数列$$x_{1}, ~ ~ x_{2}, ~ ~ x_{3}, ~ \cdots, ~ ~ x_{9}$$的公差为$$\frac{1} {2}$$,若以上述数据$$x_{1}, ~ ~ x_{2}, ~ ~ x_{3}, ~ \cdots, ~ ~ x_{9}$$为样本,则此样本的方差为()
A
A.$$\frac{5} {3}$$
B.$$\frac{1 0} {3}$$
C.$${{3}{0}}$$
D.$${{1}{0}}$$
2、['众数、中位数和平均数']正确率80.0%某中学高二$${{(}{1}{)}}$$班共有$${{5}{0}}$$名学生,其中男生$${{3}{0}}$$名,女生$${{2}{0}}$$名,采用分层抽样的方法,从全班学生中抽取$${{2}{0}}$$人测量其身高.已知在抽取的样本中,男生的平均身高为$${{a}{,}}$$女生的平均身高为$${{b}{,}}$$由此估计该班全体学生的平均身高约为()
D
A.$$\frac{a+b} {2}$$
B.$$\frac{3 a+2 b} {2}$$
C.$$\frac{2 a+3 b} {5}$$
D.$$\frac{3 a+2 b} {5}$$
3、['众数、中位数和平均数']正确率80.0%已知有$${{8}}$$个样本数据分别为$${{4}}$$,$${{7}}$$,$${{8}}$$,$${{1}{1}}$$,$${{1}{3}}$$,$${{1}{5}}$$,$${{2}{0}}$$,$${{2}{2}}$$,则估计该组数据的总体的第三四分位数为$${{(}{)}}$$
A.$${{9}}$$
B.$${{1}{2}}$$
C.$${{1}{7}{.}{5}}$$
D.$${{2}{1}}$$
4、['方差与标准差', '众数、中位数和平均数', '极差与“平均距离”']正确率60.0%已知一组样本数据$${{x}_{1}}$$,$${{x}_{2}}$$,$${{…}}$$,$$x_{1 0}$$的平均数为$${{a}}$$,由这组数据得到另一组新的样本数据$${{y}_{1}}$$,$${{y}_{2}}$$,$${{…}}$$,$$y_{1 0}$$,其中$$y_{i}=x_{i}-2$$($${{i}{=}{1}}$$,$${{2}}$$,$${{…}}$$,$${{1}{0}}$$),则()
C
A.两组样本数据的平均数相同
B.两组样本数据的方差不相同
C.两组样本数据的极差相同
D.将两组数据合成一个样本容量为$${{2}{0}}$$的新的样本数据,该样本数据的平均数为$${{a}{−}{2}}$$
5、['众数、中位数和平均数']正确率60.0%平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关,在如图所示的两种分布形态中$$, ~ a, ~ b, ~ c, ~ d$$分别对应平均数和中位数之一,则可能的对应关系是()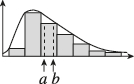
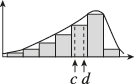
A
A.$${{a}}$$为中位数$${,{b}}$$为平均数$${,{c}}$$为平均数$${,{d}}$$为中位数
B.$${{a}}$$为平均数$${,{b}}$$为中位数$${,{c}}$$为平均数$${,{d}}$$为中位数
C.$${{a}}$$为中位数$${,{b}}$$为平均数$${,{c}}$$为中位数$${,{d}}$$为平均数
D.$${{a}}$$为平均数$${,{b}}$$为中位数$${,{c}}$$为中位数$${,{d}}$$为平均数
6、['方差与标准差', '众数、中位数和平均数']正确率40.0%一组数据的平均数是$${{3}{.}{9}}$$,方差是$${{0}{.}{9}{6}}$$,若将这组数据中的每一个数据都乘以$${{1}{0}}$$再加$${{1}}$$,得到一组新数据,则所得新数据的平均数和方差分别是()
A
A.$${{4}{0}{,}{{9}{6}}}$$
B.$${{3}{9}{,}{{9}{6}}}$$
C.$${{4}{0}{,}{{9}{.}{6}}}$$
D.$${{3}{9}{,}{{9}{.}{6}}}$$
7、['方差与标准差', '众数、中位数和平均数']正确率60.0%如果数据$$x_{1}, x_{2}, x_{3} \cdots\cdots x_{n}$$的平均值为$${{x}{¯}}$$,方差为$${{S}^{2}}$$,则$$3 x_{1}+5, \quad3 x_{2}+5, \quad3 x_{3}+5 \cdots\cdots3 x_{n}+5$$的平均值和方差分别为$${{(}{)}}$$
B
A.和$${{S}^{2}}$$
B.$$3 \overline{{x}}+5$$和$${{9}{{S}^{2}}}$$
C.$$3 \overline{{x}}+5$$和$${{S}^{2}}$$
D.$$3 \overline{{x}}+5$$和$$9 S^{2}+3 0 S+2 5$$
8、['众数、中位数和平均数', '折线图']正确率60.0%某网站为了了解某$${{“}}$$跑团$${{”}}$$每月跑步的平均里程,收集并整理了$${{2}{0}{1}{9}}$$年$${{1}}$$月至$${{2}{0}{1}{9}}$$年$${{1}{1}}$$月期间该$${{“}}$$跑团$${{”}}$$每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是 ()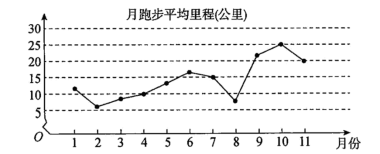
D
A.月跑步平均里程的中位数为$${{6}}$$月份对应的里程数
B.月跑步平均里程逐月增加
C.月跑步平均里程高峰期大致在$${{8}}$$,$${{9}}$$月份
D.$${{1}}$$月至$${{5}}$$月的月跑步平均里程相对于$${{6}}$$月至$${{1}{1}}$$月,波动性更小,变化比较平稳
9、['众数、中位数和平均数', '方差与标准差']正确率60.0%某人为了检测自己的解题速度,记录了$${{5}}$$次解题所花的时间(单位:分钟)分别为$$x, y, 5 5, 6 0, 5 0$$,已知这组数据的平均数为$${{5}{5}}$$,方差为$$\frac{5 2} {5}$$,则$$| x-y |=$$()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['众数、中位数和平均数']正确率80.0%甲、乙两人在一次射击比赛中各射靶$${{5}}$$次,两人成绩的条形统计图如图所示,则$${{(}{)}}$$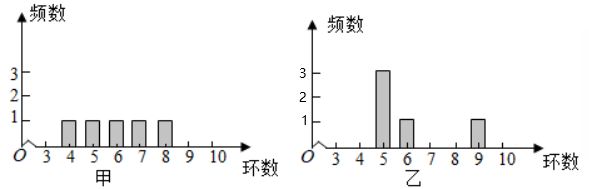
C
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
1. 对于等差数列 $$x_{1}, x_{2}, \ldots, x_{9}$$,公差为 $$\frac{1}{2}$$。样本方差的计算公式为 $$s^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2$$。由于等差数列的方差与公差有关,公式简化为 $$s^2 = \frac{(n^2 - 1)d^2}{12}$$,代入 $$n=9$$ 和 $$d=\frac{1}{2}$$,得到 $$s^2 = \frac{80}{96} = \frac{5}{3}$$。答案为 $$\boxed{A}$$。
3. 第三四分位数即第75百分位数。数据排序为 4, 7, 8, 11, 13, 15, 20, 22,共8个数。位置为 $$0.75 \times 8 = 6$$,取第6和第7个数的平均值 $$\frac{15 + 20}{2} = 17.5$$。答案为 $$\boxed{C}$$。
5. 左图右偏,平均数大于中位数,对应 $$a$$ 为平均数,$$b$$ 为中位数;右图左偏,平均数小于中位数,对应 $$c$$ 为中位数,$$d$$ 为平均数。答案为 $$\boxed{D}$$。
7. 线性变换 $$3x_i + 5$$ 的平均数为 $$3\bar{x} + 5$$,方差为 $$9S^2$$。答案为 $$\boxed{B}$$。
9. 平均数为55,故 $$x + y = 110$$。方差为 $$\frac{52}{5}$$,计算得 $$\sum (x_i - \bar{x})^2 = 52$$,代入已知数据得 $$(x - 55)^2 + (y - 55)^2 = 16$$,解得 $$|x - y| = 4$$。答案为 $$\boxed{D}$$。
.jpg)