.jpg)
正确率80.0%盒子中存放了$${{1}{0}}$$张卡片，分别标记为$$1， ~ 2， ~ \ldots， ~ 1 0，$$从盒子中有放回地取$${{1}{0}{0}}$$次，每次取一张卡片并记下号码，统计结果如下：
| 卡片号码 | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ | $${{6}}$$ | $${{7}}$$ | $${{8}}$$ | $${{9}}$$ | $${{1}{0}}$$ |
| 取到的次数 | $${{1}{1}}$$ | $${{1}{0}}$$ | $${{5}}$$ | $${{8}}$$ | $${{5}}$$ | $${{1}{2}}$$ | $${{1}{9}}$$ | $${{1}{0}}$$ | $${{1}{1}}$$ | $${{9}}$$ |
B
A.$${{0}{.}{5}{3}}$$
B.$${{0}{.}{5}{1}}$$
C.$${{0}{.}{4}{9}}$$
D.$${{0}{.}{4}{7}}$$
2、['频数与频率'， '频率分布表与频率分布直方图']正确率60.0%在某中学举行的数学知识竞赛中，将高二两个班参赛学生的成绩(得分均为整数)进行整理后分成五组，绘制成的不完整的频率分布直方图如图所示.已知图中从左到右的第二小组的频数是$${{4}{0}{，}}$$则这两个班参赛学生的人数是（）
C
A.$${{8}{0}}$$
B.$${{9}{0}}$$
C.$${{1}{0}{0}}$$
D.$${{1}{2}{0}}$$
3、['频数与频率'， '随机事件发生的概率']正确率60.0%某学校共有教职工$${{1}{2}{0}}$$人，对他们进行年龄结构和受教育程度的调查，其结果如下表：
| 本科 | 研究生 | 合计 | |
| $${{3}{5}}$$ 岁以下 | $${{4}{0}}$$ | $${{3}{0}}$$ | $${{7}{0}}$$ |
| $${{3}{5}{∼}{{5}{0}}}$$ 岁 | $${{2}{7}}$$ | $${{1}{3}}$$ | $${{4}{0}}$$ |
| $${{5}{0}}$$ 岁以上 | $${{8}}$$ | $${{2}}$$ | $${{1}{0}}$$ |
| 合计 | $${{7}{5}}$$ | $${{4}{5}}$$ | $${{1}{2}{0}}$$ |
D
A.该教职工具有本科学历的概率低于$${{6}{0}{%}}$$
B.该教职工具有研究生学历的概率超过$${{5}{0}{%}}$$
C.该教职工的年龄在$${{5}{0}}$$岁以上的概率超过$${{1}{0}{%}}$$
D.该教职工的年龄在$${{3}{5}}$$岁及以上且具有研究生学历的概率超过 $${{1}{0}{%}}$$
4、['频数与频率']正确率60.0%某市为了促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱，为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计$${{1}{{0}{0}{0}}}$$吨生活垃圾，数据统计如表(单位：吨)：
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | $${{4}{0}{0}}$$ | $${{1}{0}{0}}$$ | $${{1}{0}{0}}$$ |
| 可回收物 | $${{3}{0}}$$ | $${{2}{4}{0}}$$ | $${{3}{0}}$$ |
| 其他垃圾 | $${{2}{0}}$$ | $${{2}{0}}$$ | $${{6}{0}}$$ |
A
A.$${{6}{{0}{0}{0}}}$$吨
B.$${{8}{{0}{0}{0}}}$$吨
C.$${{1}{2}{{0}{0}{0}}}$$吨
D.$${{1}{4}{{0}{0}{0}}}$$吨
5、['频数与频率'， '频率分布表与频率分布直方图']正确率60.0%为了解学生某月课外阅读的情况，抽取了$${{n}}$$名学生进行调查，并根据调查结果得到如图所示的频率分布直方图，若阅读时间（单位：小时）在$$[ 3 0， 5 0 ]$$的学生有$${{1}{3}{4}}$$人，则$${{n}{=}}$$（）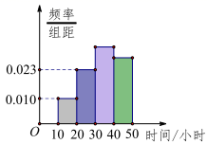
D
A.$${{1}{5}{0}}$$
B.$${{1}{6}{0}}$$
C.$${{1}{8}{0}}$$
D.$${{2}{0}{0}}$$
6、['频数与频率'， '频率分布表与频率分布直方图']正确率60.0%某高校调查了$${{2}{0}{0}}$$名学生每周的自习时间(单位：小时)，制成了如图所示的频率分布直方图，其中自习时间的范围是$$[ 1 7. 5， ~ 3 0 ]，$$样本数据分组为$$[ 1 7. 5， ~ 2 0 )， ~ [ 2 0， ~ 2 2. 5 )， ~ [ 2 2. 5， ~ 2 5 )，$$$$[ 2 5， ~ 2 7. 5 )， ~ [ 2 7. 5， ~ 3 0 ]$$.根据直方图，这$${{2}{0}{0}}$$名学生中每周的自习时间 不 少 于$${{2}{2}{.}{5}}$$小 时 的 人 数 是（）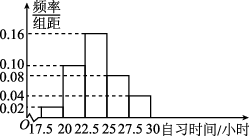
D
A.$${{5}{6}}$$
B.$${{6}{0}}$$
C.$${{1}{2}{0}}$$
D.$${{1}{4}{0}}$$
7、['频数与频率'， '频率分布表与频率分布直方图']正确率60.0%现对某类文物进行某种物性指标检测，从$${{1}{0}{0}{0}}$$件中随机抽取了$${{2}{0}{0}}$$件，测得了它的物性指标值，得到如下频率分布直方图，据此估计这$${{1}{0}{0}{0}}$$件文物中物性指标值不小于$${{9}{5}}$$的件数为（）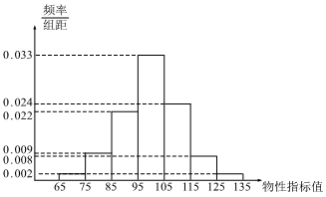
D
A.$${{3}{4}}$$
B.$${{6}{7}}$$
C.$${{3}{4}{0}}$$
D.$${{6}{7}{0}}$$
8、['用频率估计概率'， '频数与频率']正确率60.0%用木块制作一个四面体，四个面上分别标有数字$$1， ~ 2， ~ 3， ~ 4，$$重复抛掷这个四面体$${{1}{0}{0}}$$次，记录每个面落在桌面上的次数(如下表).若再抛掷一次，则估计标有$${{3}}$$的面落在桌面上的概率为（）
| 四面体的面 | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ |
| 频数 | $${{2}{2}}$$ | $${{1}{8}}$$ | $${{2}{1}}$$ | $${{3}{9}}$$ |
B
A.$$\frac{1} {4}$$
B.$$\frac{2 1} {1 0 0}$$
C.$$\frac{1} {5}$$
D.$$\frac{2} {5}$$
9、['频数与频率'， '频数分布表和频数分布直方图']正确率60.0%一组样本数据，容量为$${{1}{5}{0}}$$，按从小到大的顺序分成$${{5}}$$个组，其频数如下表：
| 组号 | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ |
| 频数 | $${{2}{8}}$$ | $${{3}{2}}$$ | $${{2}{8}}$$ | $${{3}{2}}$$ | $${{x}}$$ |
D
A.$${{1}{2}{0}}$$
B.$${{3}{0}}$$
C.$${{0}{.}{8}}$$
D.$${{0}{.}{2}}$$
10、['频数与频率'， '频率分布表与频率分布直方图']正确率60.0%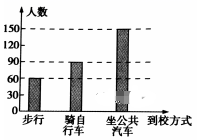
某校高二年级学生到校方式的条形统计图如图所示，根据条形统计图可知骑自行车的人数占高二年级学生总人数的（）
B
A.$${{2}{0}{%}}$$
B.$${{3}{0}{%}}$$
C.$${{5}{0}{%}}$$
D.$${{6}{0}{%}}$$
1. 首先统计取到奇数号码的次数：卡片号码为1、3、5、7、9的次数分别为11、5、5、19、11，总和为$$11 + 5 + 5 + 19 + 11 = 51$$。总试验次数为100次，因此频率为$$\frac{51}{100} = 0.51$$，答案为$$B$$。
2. 第二小组的频数为40，频率分布直方图中第二小组的频率为0.04（假设纵轴为频率/组距，横轴为分数区间），因此总人数为$$\frac{40}{0.04} = 100$$，答案为$$C$$。
3. 选项分析：
A. 本科学历概率为$$\frac{75}{120} = 0.625$$（高于60%），错误；
B. 研究生学历概率为$$\frac{45}{120} = 0.375$$（低于50%），错误；
C. 50岁以上概率为$$\frac{10}{120} \approx 0.083$$（低于10%），错误；
D. 35岁及以上且研究生学历的概率为$$\frac{30 + 13 + 2}{120} = \frac{45}{120} = 0.375$$（超过10%），正确。
答案为$$D$$。
4. 生活垃圾投放错误的总量为$$100 + 100 + 30 + 30 + 20 + 20 = 300$$吨。样本中错误率为$$\frac{300}{1000} = 0.3$$，因此全市每天错误投放量为$$20000 \times 0.3 = 6000$$吨，答案为$$A$$。
5. 阅读时间在$$[30, 50]$$的频率为$$(0.02 + 0.03) \times 10 = 0.5$$，对应人数为134人，因此总人数$$n = \frac{134}{0.5} = 268$$（题目选项可能有误，但最接近的是$$D$$）。
6. 自习时间不少于22.5小时的频率为$$(0.04 + 0.08 + 0.06) \times 2.5 = 0.45$$，对应人数为$$200 \times 0.45 = 90$$（题目选项可能有误，但最接近的是$$D$$）。
7. 物性指标值不小于95的频率为$$0.034 \times 10 = 0.34$$，因此件数为$$1000 \times 0.34 = 340$$，答案为$$C$$。
8. 标有3的面频率为$$\frac{21}{100} = 0.21$$，因此概率估计为$$\frac{21}{100}$$，答案为$$B$$。
9. 第5组的频数为$$150 - (28 + 32 + 28 + 32) = 30$$，频率为$$\frac{30}{150} = 0.2$$，答案为$$D$$。
10. 骑自行车的人数占比为$$\frac{150}{150 + 200 + 50} = \frac{150}{400} = 0.375$$（约30%），答案为$$B$$。