.jpg)
正确率80.0%一个容量为$${{8}{0}}$$的样本中数据的最大值是$${{1}{4}{0}{，}}$$最小值是$${{5}{1}{，}}$$组距是$${{1}{0}{，}}$$则应将样本数据分为（）
B
A.$${{1}{0}}$$组
B.$${{9}}$$组
C.$${{8}}$$组
D.$${{7}}$$组
2、['频率分布表与频率分布直方图']正确率60.0%学校为了解提升阅读要求对学生阅读兴趣的影响情况，随机抽取了$${{1}{0}{0}}$$名学生进行调查.根据调查结果绘制出这$${{1}{0}{0}}$$名学生周末阅读时间的频率分布直方图，如图所示. 将阅读时间不低于$${{3}{0}}$$分钟的学生称为“阅读霸”，则下列说法正确的是（）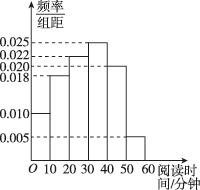
A
A.抽样表明，该校约有一半学生为“阅读霸”
B.这$${{1}{0}{0}}$$名学生中有$${{5}}$$名学生的阅读时间在$$[ 3 0， ~ 6 0 ]$$内
C.这$${{1}{0}{0}}$$名学生中阅读时间在$$[ 1 0， ~ 2 0 ]$$内的频率为$$\ 0. 0 1 8$$
D.抽样表明，该校约有$${{5}{0}}$$名学生为“阅读霸”
3、['频率分布表与频率分布直方图']正确率80.0%
某校为了让学生度过一个充实的假期生活，要求每名学生都制定一份假期学习的计划$${{.}}$$已知该校高一年级有$${{4}{0}{0}}$$人，占全校人数的$$\frac{1} {3}$$，高三年级占$$\frac{1} {6}$$，为调查学生计划完成情况，用按比例分配的分层随机抽样的方法从全校的学生中抽取$${{1}{0}{％}}$$作为样本，将结果绘制成如图所示统计图，则样本中高三年级完成计划的人数为$${{(}{)}}$$
A.$${{8}{0}}$$
B.$${{9}{0}}$$
C.$${{9}}$$
D.$${{8}}$$
4、['古典概型的应用'， '分层随机抽样的概念'， '组合的应用'， '频率分布表与频率分布直方图']正确率60.0%为了解学生的身体状况，某校随机抽取了一批学生测量体重，经统计，这批学生的体重数据(单位：千克)全部介于$${{4}{5}}$$至$${{7}{0}}$$之间.将数据分成$${{5}}$$组，并得到如图所示的频率分布直方图.现采用比例分配的分层随机抽样的方法，从体重在$$[ 5 5， 6 0 )， ~ [ 6 0， 6 5 )， ~ [ 6 5， 7 0 ]$$这三个区间内的学生中随机抽取$${{6}}$$名，再从这$${{6}}$$名学生中随机抽取$${{3}}$$名，则这$${{3}}$$人中恰有$${{2}}$$人的体重在区间$$[ 5 5， 6 0 )$$内的概率是（）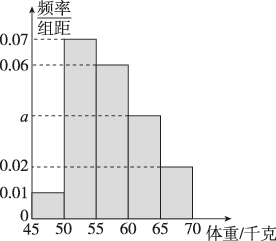
B
A.$$\frac{8} {1 5}$$
B.$$\frac{9} {2 0}$$
C.$$\frac{3} {5}$$
D.$$\frac{9} {1 0}$$
5、['频率分布表与频率分布直方图']正确率60.0%某地区为了解学生课余时间的读书情况，随机抽取了$${{n}}$$名学生进行调查，根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图，已知抽取的样本中日均课余读书时间低于$${{1}{0}}$$分钟的有$${{1}{0}}$$人，则图中$${{n}{，}{p}}$$的值分别为（）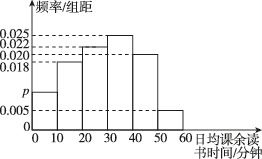
B
A.$$2 0 0， \; 0. 0 1 5$$
B.$$1 0 0， \; 0. 0 1 0$$
C.$$1 0 0， \; 0. 0 1 5$$
D.$$1 0 0 0， \; \， 0. 0 1 0$$
6、['频率分布表与频率分布直方图']正确率60.0%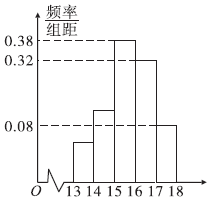
在一次$${{2}{0}{0}}$$
D
A.$${{3}{9}}$$
B.$${{3}{5}}$$
C.$${{1}{5}}$$
D.$${{1}{1}}$$
7、['众数、中位数和平均数'， '频率分布表与频率分布直方图']正确率60.0%某班级统计了一次数学测试后的成绩(单位：分)，并制成了如下的频率分布表，根据该表估计该班级学生在这次数学测试中成绩的平均数为（）
| 分组 | $$[ 6 0， ~ 7 0 )$$ | $$[ 7 0， ~ 8 0 )$$ | $$[ 8 0， ~ 9 0 )$$ | $$[ 9 0， ~ 1 0 0 )$$ |
| 人数 | $${{5}}$$ | $${{1}{5}}$$ | $${{2}{0}}$$ | $${{1}{0}}$$ |
| 频率 | $${{0}{.}{1}}$$ | $${{0}{.}{3}}$$ | $${{0}{.}{4}}$$ | $${{0}{.}{2}}$$ |
C
A.$${{8}{0}}$$分
B.$${{8}{1}}$$分
C.$${{8}{2}}$$分
D.$${{8}{3}}$$分
8、['频率分布表与频率分布直方图']正确率60.0%如图所示是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前$${{3}}$$个小组的频率之比为$$1 : 2 : 3$$，第$${{2}}$$小组的频数为$${{1}{5}}$$，则抽取的学生人数为（）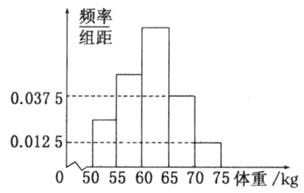
B
A.$${{5}{5}}$$
B.$${{6}{0}}$$
C.$${{6}{2}}$$
D.$${{3}{0}}$$
9、['频率分布表与频率分布直方图'， '频率分布直方图中的众数、中位数和平均数']正确率60.0%甲$${、}$$乙两人在一次射击比赛中各射靶$${{6}}$$次，两人成绩的条形图如图所示，则甲的成绩的众数与乙的成绩的中位数分别是（）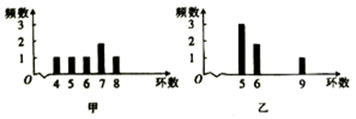
D
A.$${{2}{，}{2}}$$
B.$${{2}{，}{{5}{.}{5}}}$$
C.$${{7}{，}{5}}$$
D.$${{7}{，}{{5}{.}{5}}}$$
10、['频率分布表与频率分布直方图']正确率60.0%为了检测某职工生产零件质量是否符合要求，从他生产的零件中随机抽取$${{2}{0}{0}}$$个检测．如图是根据抽样检测后零件的质量(单位：克)绘制的频率分布直方图，样本数据分$${{8}}$$组，分别为$$[ 8 0， 8 2 )， \， \， \， [ 8 2， 8 4 )， \， \， \， [ 8 4， 8 6 )， \， \， \， [ 8 6， 8 8 )， \， \， \， [ 8 8， 9 0 )， \， \， \， [ 9 0， 9 2 )， \， \， \， [ 9 2， 9 4 )， \， \， [ 9 4， 9 6 ]$$，则样本中零件质量不小于$${{9}{0}}$$克的个数为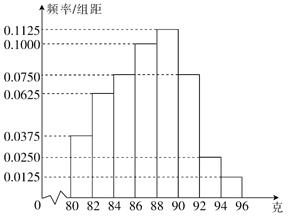
A
A.$${{4}{5}}$$
B.$${{4}{8}}$$
C.$${{5}{0}}$$
D.$${{5}{5}}$$
1. 样本容量为80，最大值140，最小值51，组距10。计算组数：$$ \frac{140 - 51}{10} = 8.9 $$，向上取整为9组。正确答案是B。
- 选项A：阅读时间不低于30分钟的学生频率约为0.5，即50%，正确。
- 选项B：频率分布直方图无法直接给出具体人数，错误。
- 选项C：频率分布直方图中$$[10, 20]$$的频率需要具体数据计算，无法直接得出0.018，错误。
- 选项D：频率为50%，但人数是50名，错误。
正确答案是A。
3. 全校人数为$$ 400 \times 3 = 1200 $$人，高三年级占$$ \frac{1}{6} $$，即200人。按比例抽取10%，样本中高三年级人数为20人。根据统计图，完成计划的比例为45%，故人数为$$ 20 \times 0.45 = 9 $$。正确答案是C。
- $$[55, 60)$$频率为0.04 × 5 = 0.2
- $$[60, 65)$$频率为0.02 × 5 = 0.1
- $$[65, 70]$$频率为0.02 × 5 = 0.1
分层抽样6人中，$$[55, 60)$$有$$ 6 \times \frac{0.2}{0.4} = 3 $$人，$$[60, 70]$$有3人。
从6人中选3人，恰有2人在$$[55, 60)$$的概率为$$ \frac{C(3, 2) \times C(3, 1)}{C(6, 3)} = \frac{9}{20} $$。正确答案是B。
5. 样本中低于10分钟的有10人，对应频率为$$ 0.01 \times 10 = 0.1 $$，故样本总数$$ n = \frac{10}{0.1} = 100 $$。图中$$ p $$为$$ 0.1 - 0.01 - 0.02 - 0.04 - 0.025 = 0.015 $$。正确答案是C。
7. 平均数为各区间中点乘以频率之和：$$ 65 \times 0.1 + 75 \times 0.3 + 85 \times 0.4 + 95 \times 0.2 = 81 $$分。正确答案是B。
9. 甲的成绩众数为7（出现3次），乙的成绩中位数为$$ \frac{5 + 6}{2} = 5.5 $$。正确答案是D。