.jpg)
正确率60.0%数列$$0，-\frac{7} {5}， \frac{1 3} {5}，-\frac{6 3} {1 7}， \cdots$$的一个通项公式是$${{(}{)}}$$
A
A.$$(-1 )^{n+1} \， \frac{n^{3}-1} {n^{2}+1}$$
B.$$(-1 )^{n} \frac{n^{3}-1} {n^{2}+1}$$
C.$$(-1 )^{n-1} \， \frac{n^{3}-1} {n^{2}-1}$$
D.$$(-1 )^{n} \frac{n^{3}-1} {n^{2}-1}$$
2、['归纳推理']正确率40.0%把数列$${{\{}{{a}_{n}}{\}}}$$的各项按顺序排列成如下的三角形状，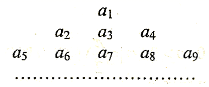
记$$A ~ ( i， ~ j )$$
B
A.$${{3}{6}}$$
B.$${{3}{7}}$$
C.$${{3}{8}}$$
D.$${{4}{5}}$$
3、['归纳推理']正确率60.0%现有四种不同的图案按如下规律进行排列
其中第$${{1}}$$
B
A.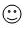
B.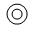
C.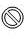
D.
正确率60.0%当$$a， ~ b \in\mathbf{R}$$且$${{b}{≠}{0}}$$时，有$$| \frac{a} {b} |=\frac{| a |} {| b |}$$成立．某学生据此得出，当$$z_{1}， ~ z_{2} \in{\bf C}$$且$${{z}_{2}{≠}{0}}$$时，有$$| \frac{z_{1}} {z_{2}} |=\frac{| z_{1} |} {| z_{2} |}$$成立．该生的推理是（）
C
A.演绎推理
B.三段论
C.类比推理
D.归纳推理
5、['归纳推理']正确率60.0%某次数学考试成绩公布后，甲$${、}$$乙$${、}$$丙$${、}$$丁四人谈论成绩情况．甲说：$${{“}}$$我们四个人的分数都不一样，但我和乙的成绩之和等于丙$${、}$$丁两人的成绩之和$${{”}}$$，乙说：$${{“}}$$丙$${、}$$丁两人中一人分数比我高，一人分数比我低$${{”}}$$，丙说：$${{“}}$$我的分数不是最高的$${{”}}$$，丁说：$${{“}}$$我的分数不是最低的$${{”}}$$，则四人中成绩最高的是（）
D
A.甲
B.乙
C.丙
D.丁
6、['归纳推理']正确率40.0%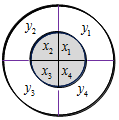
已知两个半径不等的圆盘叠放在一起（有一轴穿过它们的圆心），两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为$$x_{1}， ~ x_{2}， ~ x_{3}， ~ x_{4}$$
A
A.$$T_{1}， ~ T_{2}， ~ T_{3}， ~ T_{4}$$中至少有一个为正数
B.$$T_{1}， ~ T_{2}， ~ T_{3}， ~ T_{4}$$中至少有一个为负数
C.$$T_{1}， ~ T_{2}， ~ T_{3}， ~ T_{4}$$中至多有一个为正数
D.$$T_{1}， ~ T_{2}， ~ T_{3}， ~ T_{4}$$中至多有一个为负数
7、['归纳推理']正确率40.0%观察下列算式：
$${{1}^{3}{=}{1}}$$，
$$2^{3}=3+5$$，
$$3^{3}=7+9+1 1$$，
$$4^{3}=1 3+1 5+1 7+1 9$$，
$${{…}}$$
若某数$${{n}^{3}}$$按上述规律展开后，发现等式右边含有$${{“}{{2}{0}{1}{3}}{”}}$$这个数，则$${{n}{=}{（}}$$）
C
A.$${{4}{1}}$$
B.$${{4}{3}}$$
C.$${{4}{5}}$$
D.$${{4}{7}}$$
8、['归纳推理']正确率60.0%灯会，是中国一种古老的民俗文化，一般指春节前后至元宵节时，由官方举办的大型的灯饰展览活动，并常常附带有一些猜灯谜等活动，极具传统性和地方特色．春节期间，某校甲$${、}$$乙$${、}$$丙$${、}$$丁四位同学相约来猜灯谜，每人均获得一次机会．游戏开始前，甲$${、}$$乙$${、}$$丙$${、}$$丁四位同学对游戏中奖结果进行了预测，预测结果如下：
甲说：$${{“}}$$我或乙能中奖$${{”}}$$；乙说：$${{“}}$$丁能中奖$${{”}^{′}}$$；
丙说：$${{“}}$$我或乙能中奖$${{”}}$$；丁说：$${{“}}$$甲不能中奖$${{”}}$$．
游戏结束后，这四位同学中只有一位同学中奖，且只有一位同学的预测结果是正确的，则中奖的同学是（）
A
A.甲
B.乙
C.丙
D.丁
9、['归纳推理']正确率60.0%若$$f ( n )=$$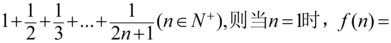
$${{(}{)}}$$
C
A.$${{1}}$$
B.$$\frac{1} {3}$$
C.$$1+\frac{1} {2}+\frac{1} {3}$$
D.都不正确
10、['归纳推理']正确率40.0%观察下列式子：$$1+\frac{1} {2^{2}} < ~ \frac{3} {2}， ~ 1+\frac{1} {2^{2}}+\frac{1} {3^{2}} < ~ \frac{5} {3}， ~ 1+\frac{1} {2^{2}}+$$$$\frac{1} {3^{2}}+\frac{1} {4^{2}} < \frac{7} {4}， \ldots$$.根据以上式子可以猜想：$$1+\frac1 {2^{2}}+\frac1 {3^{2}}+\ldots+\frac1 {2 \， 0 1 9^{2}} <$$（）
C
A.$$\frac{4 \; 0 3 5} {2 \; 0 1 9}$$
B.$$\frac{4 \; 0 3 6} {2 \; 0 1 9}$$
C.$$\frac{4 \; 0 3 7} {2 \; 0 1 9}$$
D.$$\frac{4 \; 0 3 8} {2 \; 0 1 9}$$
1. 首先观察数列的前几项：$$0, -\frac{7}{5}, \frac{13}{5}, -\frac{63}{17}, \cdots$$。我们需要找到一个通项公式，使得当$$n=1,2,3,4$$时，公式的值分别对应这些项。
2. 观察题目中的三角形状排列，可以发现每一行的数字个数等于行数。例如，第一行1个数字，第二行2个数字，第三行3个数字，依此类推。我们需要找到$$A(i, j)$$的位置。
3. 观察图案的排列规律，可以发现图案按顺序循环排列。题目中给出了四种不同的图案，假设它们的顺序为$$A, B, C, D$$，然后循环重复。
4. 题目描述了一个学生从实数性质推广到复数性质的推理过程。实数中$$|\frac{a}{b}| = \frac{|a|}{|b|}$$，学生类比到复数中$$|\frac{z_1}{z_2}| = \frac{|z_1|}{|z_2|}$$。
5. 根据题目描述，甲、乙、丙、丁四人的分数各不相同，且满足以下条件： - 甲和乙的成绩之和等于丙和丁的成绩之和； - 乙的成绩在丙和丁之间； - 丙的成绩不是最高的； - 丁的成绩不是最低的。