.jpg)
正确率40.0%以下四个命题中是假命题的是$${{(}{)}}$$
D
A.$${{“}}$$昆虫都是$${{6}}$$条腿，竹节虫是昆虫，所以竹节虫有$${{6}}$$条腿$${{”}}$$此推理属于演绎推理．
B.$${{“}}$$在平面中，对于三条不同的直线$$a， ~ b， ~ c$$，若$$a / / b， ~ b / / c$$则$${{a}{/}{/}{c}}$$，将此结论放到空间中也成立$${{”}}$$此推理属于合情推理．
C.
是$${{“}}$$函数$$f ( x )=a x+l n x$$存在极值$${{”}}$$的必要不充分条件．
D.若$$x \in( 0， \ \frac{\pi} {2} ]$$，则$$\operatorname{s i n} x+\frac{2} {\operatorname{s i n} x}$$的最小值为$${{2}{\sqrt {2}}}$$．
2、['决定系数R^2'， '演绎推理'， '随机事件发生的概率'， '随机事件'， '命题的真假性判断']正确率40.0%下列说法正确的个数有$${{(}{)}}$$
$${①}$$用$$R^{2}=1-\frac{\sum_{i=1}^{n} ( y_{i}-\hat{y}_{i} )^{2}} {\sum_{i=1}^{n} ( y_{i}-\bar{y} )^{2}}$$刻画回归效果，当$${{R}^{2}}$$越大时，模型的拟合效果越差；反之，则越好
$${②{"}}$$已知碱金属都能与水发生还原反应，钠为碱金属，所以钠能与水发生反应$${{"}}$$是演绎推理
$${③}$$一枚硬币掷一次得到正面的概率是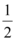
，那么掷两次一定会出现一次正面的情况
$${④}$$
A
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
3、['演绎推理']正确率60.0%以下三句话可组成一个三段论：$${}^{\iota^{\iota}} \Diamond\; y=\operatorname{t a n} x$$是三角函数；$${②}$$三角函数是周期函数；$$\odot\， y=\operatorname{t a n} x$$是周期函数$${{”}}$$．其中大前提的序号是（）
B
A.$${①}$$
B.$${②}$$
C.$${③}$$
D.$${①}$$和$${②}$$
4、['演绎推理']正确率60.0%若大前提是：任何实数的平方都大于$${{0}}$$，小前提是：$${{a}{∈}{R}}$$，结论是：$${{a}^{2}{>}{0}}$$，那么这个演绎推理所得结论错误的原因是（）
A
A.大前提错误
B.小前提错误
C.推理形式错误
D.大前提小前提都错
5、['演绎推理']正确率60.0%正弦函数是奇函数，$${{y}{=}{{c}{o}{s}}{x}}$$是正弦函数，因此$${{y}{=}{{c}{o}{s}}{x}}$$是奇函数，以上推理
C
A.结论正确
B.大前提不正确
C.小前提不正确
D.全不正确
6、['类比推理'， '演绎推理'， '命题的真假性判断']正确率40.0%下面结论正确的是（）
$${①{“}}$$所有$${{2}}$$的倍数都是$${{4}}$$的倍数，某数$${{m}}$$是$${{2}}$$的倍数，则$${{m}}$$一定是$${{4}}$$的倍数$${{”}}$$，这是三段论推理，但其结论是错误的．
$${②}$$在类比时，平面中的三角形与空间中的平行六面体作为类比对象较为合适．
$${③}$$由平面三角形的性质推测空间四面体的性质，这是一种合情推理．
$${④}$$一个数列的前三项是$$1， ~ 2， ~ 3$$，那么这个数列的通项公式必为$$a_{n}=n \ ( \ n \in N * )$$．
A
A.$${①{③}}$$
B.$${②{③}}$$
C.$${③{④}}$$
D.$${②{④}}$$
7、['类比推理'， '演绎推理'， '分析法'， '归纳推理']正确率40.0%下面几种推理过程是演绎推理的是$${{(}{)}}$$
C
A.某校高二年级有$${{1}{0}}$$个班，$${{1}}$$班$${{6}{2}}$$人，$${{2}}$$班$${{6}{1}}$$人，$${{3}}$$班$${{6}{2}}$$人，由此推测各班人数都超过$${{6}{0}}$$人
B.根据三角形的性质，可以推测空间四面体的性质
C.平行四边形对角线互相平分，矩形是平行四边形，所以矩形的对角线互相平分
D.在数列$${{\{}{{a}_{n}}{\}}}$$中，$${\bf a_{1}=1， a_{n+1}=} \frac{{\bf2 a_{n}}} {{\bf2+a_{n}}}， {\bf n} \in\bf{^{*}}$$，计算$$\mathbf{a_{2}}， \mathbf{a_{3}}，$$由此归纳出$${{\{}{{a}_{n}}{\}}}$$的通项公式
8、['函数的新定义问题'， '演绎推理'， '对数的运算性质'， '对数的换底公式及其推论']正确率60.0%$${{1}{8}{5}{9}}$$年，德国数学家黎曼向德国科学院提交了题目为$${《}$$论小于某值的素数个数$${》}$$的论文并提出了一个命题，这个命题就是著名的黎曼猜想.在此之前，著名数学家欧拉也研究过这个问题，并得到了小于正整数$${{x}}$$的素数个数大约可以表示为$$\pi( x ) \approx\frac{x} {\operatorname{l n} x}$$的结论，根据欧拉的结论，估计$$1 0 0 0 0$$以内的素数个数大约是（）
(素数即质数，$$\mathrm{l g} e \approx0. 4 3 4 2 9$$，计算结果四舍五入取整数)
A
A.$${{1}{0}{8}{6}}$$
B.$${{1}{0}{8}{5}}$$
C.$${{1}{4}{4}{7}}$$
D.$${{1}{4}{4}{8}}$$
9、['演绎推理']正确率60.0%下列三句话按三段论的模式排列顺序正确的是（）
$${①{{2}{0}{1}{8}}}$$ 能被 $${{2}}$$ 整除； $${②}$$ 一切偶数都能被 $${{2}}$$ 整除； $${③{{2}{0}{1}{8}}}$$ 是偶数；
C
A.$${①{②}{③}}$$
B.$${②{①}{③}}$$
C.$${②{③}{①}}$$
D.$${③{②}{①}}$$
10、['演绎推理']正确率60.0%推理$${{“}{①}}$$正方形是菱形；$${②}$$等腰梯形是正方形；$${③}$$等腰梯形是菱形$${{”}}$$中的小前提是（）
B
A.$${①}$$
B.$${②}$$
C.$${③}$$
D.$${①}$$和$${②}$$
1. 解析：
选项A：演绎推理是从一般到特殊的推理，昆虫都是6条腿是大前提，竹节虫是昆虫是小前提，结论正确，推理形式正确，是真命题。
选项B：平行线的传递性在平面和空间中都成立，但这是由数学公理直接推导的，属于演绎推理而非合情推理，因此是假命题。
选项C：$$f(x) = a x + \ln x$$存在极值的必要条件是导数有零点，即$$f'(x) = a + \frac{1}{x} = 0$$有解，解得$$a < 0$$，但还需验证是否为极值点，因此是必要不充分条件，是真命题。
选项D：当$$x \in (0, \frac{\pi}{2}]$$时，$$\sin x \in (0,1]$$，但$$\sin x + \frac{2}{\sin x} \geq 2\sqrt{2}$$在$$\sin x = \sqrt{2}$$时成立，而$$\sqrt{2} \notin (0,1]$$，最小值实际在$$\sin x = 1$$时取得，值为3，因此是假命题。
综上，假命题是B和D，但题目要求选择一个，可能是B。
2. 解析：
① $$R^2$$越大，模型的拟合效果越好，因此①错误。
② 这是从一般到特殊的推理，属于演绎推理，正确。
③ 掷两次硬币不一定出现正面，概率为$$1 - \left(\frac{1}{2}\right)^2 = \frac{3}{4}$$，因此③错误。
④ 题目不完整，无法判断。
综上，只有②正确，选A。
3. 解析：
大前提是“三角函数是周期函数”，小前提是“$$y = \tan x$$是三角函数”，结论是“$$y = \tan x$$是周期函数”。因此大前提是②，选B。
4. 解析：
大前提“任何实数的平方都大于0”错误，因为$$0^2 = 0$$，选A。
5. 解析：
小前提“$$y = \cos x$$是正弦函数”错误，因为余弦函数不是正弦函数，选C。
6. 解析：
① 结论错误，因为2的倍数不一定是4的倍数，但推理形式是三段论，正确。
② 三角形应与四面体类比，平行六面体不合适，错误。
③ 由平面到空间的推理是合情推理，正确。
④ 数列前三项为1, 2, 3，通项公式不唯一，错误。
综上，①③正确，选A。
7. 解析：
A是归纳推理，B是类比推理，D是归纳推理，C是从一般到特殊的演绎推理，选C。
8. 解析：
根据欧拉公式，$$\pi(10000) \approx \frac{10000}{\ln 10000}$$，$$\ln 10000 = 4 \ln 10 \approx 4 \times 2.3026 = 9.2104$$，因此$$\pi(10000) \approx \frac{10000}{9.2104} \approx 1085.7$$，四舍五入为1086，选A。
9. 解析：
三段论的正确顺序是大前提、小前提、结论，即②→③→①，选C。
10. 解析：
小前提是“等腰梯形是正方形”，即②，选B。