.jpg)
正确率80.0%“以直代曲”是重要的数学思想$${{.}}$$具体做法是：在函数图像某个切点附近用切线代替曲线来近似计算$${{.}}$$比如要求$${{s}{i}{n}{{0}{.}{0}{5}}}$$的近似值，我们可以先构造函数$${{y}{=}{{s}{i}{n}}{x}}$$，由于$${{0}{.}{0}{5}}$$与$${{0}}$$比较接近，所以求出$${{x}{=}{0}}$$处的切线方程为$${{y}{=}{x}}$$，再把$${{x}{=}{{0}{.}{0}{5}}}$$代入切线方程，故有$$\operatorname{s i n} 0. 0 5 \approx0. 0 5$$，类比上述方式，则$$e^{\frac{1} {1 0 0 0}} \approx( \begin{array} {c c} {} & {} \\ {} & {} \\ \end{array} )$$
A.$$\mathrm{1. 0 0 1}$$
B.$$1. 0 0 5$$
C.$$1. 0 1 5$$
D.$$1. 0 2 5$$
2、['统计图表分析'， '合情推理与演绎推理'， '频率分布表与频率分布直方图']正确率80.0%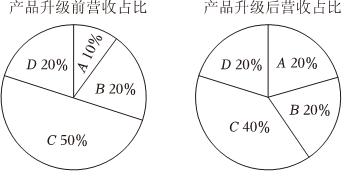
某企业对目前销售的$${{A}}$$，$${{B}}$$，$${{C}}$$，$${{D}}$$四种产品进行改造升级，经过改造升级后，企业营收实现翻番，现统计了该企业升级前后四种产品的营收占比，得到如图饼图：下列说法正确的是$${{(}{)}}$$
A.产品升级后，产品$${{A}}$$的营收是升级前的$${{2}}$$倍
B.产品升级后，产品$${{B}}$$的营收不变
C.产品升级后，产品$${{C}}$$的营收减少
D.产品升级后，产品$${{B}}$$，$${{D}}$$的营收的总和占总营收的比例不变
3、['合情推理与演绎推理'， '总体百分位数的估计']正确率40.0%数据$${{8}}$$，$${{6}}$$，$${{5}}$$，$${{2}}$$，$${{7}}$$，$${{9}}$$，$${{1}{2}}$$，$${{4}}$$，$${{1}{2}}$$的第$${{4}{0}}$$百分位数是$${{(}{)}}$$
A.$${{5}}$$
B.$${{6}}$$
C.$${{7}{.}{5}}$$
D.$${{8}}$$
4、['合情推理与演绎推理']正确率80.0%
如图展示的是一个树形图的从上至下的前$${{6}}$$行生长过程，依据图中所示的生长规律，第$${{1}{0}}$$行的圆圈个数是$${{(}{)}}$$
A.$${{5}{5}}$$
B.$${{3}{4}}$$
C.$${{2}{1}}$$
D.$${{1}{3}}$$
5、['合情推理与演绎推理']正确率80.0%某班举行了一次有意思的智力竞猜游戏，首先老师将三只冬奥会吉祥物冰墩墩进行了$${{1}}$$、$${{2}}$$、$${{3}}$$三个数字的标号，然后将它们放入不透明的箱子中，甲、乙、丙三名同学分别进行抽取，并将抽到的冰墩墩的标号告知老师，老师根据三人抽取的号码情况给出了三种说法：
①甲抽取的是$${{1}}$$号冰墩墩；
②乙抽取的不是$${{2}}$$号冰墩墩；
③丙抽取的不是$${{1}}$$号冰墩墩．
若三种说法中只有一个说法正确，则抽取$${{2}}$$号冰墩墩的是$${{(}{)}}$$
A.甲
B.乙
C.丙
D.无法判定
6、['合情推理与演绎推理']正确率80.0%已知数列$${{0}}$$，$${{l}{g}{3}}$$，$${{l}{g}{5}}$$，$${{l}{g}{7}}$$，…，根据该数列的规律，该数列中小于$${{2}}$$的项有$${{(}{)}}$$
A.$${{5}{0}}$$项
B.$${{5}{1}}$$项
C.$${{1}{0}{0}}$$项
D.$${{1}{0}{1}}$$项
7、['合情推理与演绎推理']正确率80.0%分形几何学是一门以不规则几何形态为研究对象的几何学，它的研究对象普遍存在于自然界中，因此又被称为“大自然的几何学”$${{.}}$$按照如图$${{1}}$$所示的分形规律，可得如图$${{2}}$$所示的一个树形图$${{.}}$$若记图$${{2}}$$中第$${{n}}$$行黑圈的个数为$${{a}_{n}}$$，则$$a_{7}=( \begin{array} {c} {} \\ \end{array} )$$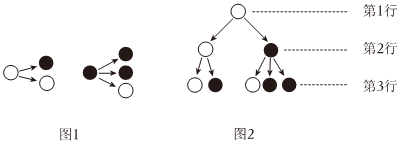
A.$${{1}{1}{0}}$$
B.$${{1}{2}{8}}$$
C.$${{1}{4}{4}}$$
D.$${{8}{9}}$$
8、['合情推理与演绎推理']正确率80.0%我国古代数学名著《九章算术》的论割圆术中有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，它体现了一种无限与有限的转化过程．比如在$$1+\frac{1} {1+\frac{1} {1+\cdots}}$$表达式中“…”既代表无限次重复，但原式却又是个定值，它可以通过方程$$1+\frac{1} {x}=x$$解得$$x=\frac{\sqrt{5}+1} {2}$$，类比上述方法，则$$\sqrt{2+\sqrt{2+\sqrt{\dots}}}=( \begin{array} {c} {\mu} \\ \end{array} )$$
A.$$\frac{{\sqrt5}-1} {2}$$
B.$$\frac{{\sqrt5}+1} {2}$$
C.$${\sqrt {2}}$$
D.$${{2}}$$
9、['合情推理与演绎推理']正确率40.0%数学探究课上，某同学发现借助多项式运算可以更好地理解“韦达定理”$${{.}}$$若$${{x}_{1}}$$，$${{x}_{2}}$$，$${{x}_{3}}$$为方程$$a x^{3}+b x^{2}+c x+d=0 ( a \neq0 )$$的$${{3}}$$个实数根，设$$a x^{3}+b x^{2}+c x+d=a ( x-x_{1} ) ( x-x_{2} ) ( x-x_{3} )$$，则$$- a ( x_{1}+x_{2}+x_{3} )$$为$${{x}^{2}}$$的系数，$$a ( x_{1} x_{2}+x_{1} x_{3}+x_{2} x_{3} )$$为$${{x}}$$的系数，$$- a x_{1} x_{2} x_{3}$$为常数项，于是有$$x_{1}+x_{2}+x_{3}=-\frac{b} {a}$$，$$x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=\frac{c} {a}$$，$$x_{1} x_{2} x_{3}=-\frac{d} {a}.$$实际上任意实系数$${{n}}$$次方程都有类似结论$${{.}}$$设方程$$( x-1 )^{4}+( x-1 )^{3}-7 ( x-1 )^{2}+5=0$$的四个实数根为$${{x}_{1}}$$，$${{x}_{2}}$$，$${{x}_{3}}$$，$${{x}_{4}}$$，则$${{(}{)}}$$
A.$$x_{1}+x_{2}+x_{3}+x_{4}=-1$$
B.$$x_{1} x_{2} x_{3} x_{4}=-5$$
C.$$x_{1} x_{2} x_{3} x_{4}=5$$
D.$$x_{1}+x_{2}+x_{3}+x_{4}=3$$
10、['合情推理与演绎推理']正确率80.0%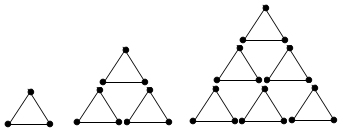
如图所示的是某小朋友在用火柴拼图时呈现的图形，其中第$${{1}}$$个图形用了$${{3}}$$根火柴，第$${{2}}$$个图形用了$${{9}}$$根火柴，第$${{3}}$$个图形用了$${{1}{8}}$$根火柴，……，按此规律，则第$${{2}{0}{2}{1}}$$个图形用的火柴根数为$${{(}{)}}$$
A.$$2 0 1 9 \times2 0 2 0$$
B.$$2 0 1 9 \times2 0 2 1$$
C.$$3 0 3 0 \times2 0 2 1$$
D.$$3 0 3 3 \times2 0 2 1$$
1. 解析：
题目要求用“以直代曲”的方法近似计算 $$e^{\frac{1}{1000}}$$。构造函数 $$y = e^x$$，在 $$x = 0$$ 处的切线方程为 $$y = 1 + x$$。将 $$x = \frac{1}{1000}$$ 代入切线方程，得到近似值 $$1 + \frac{1}{1000} = 1.001$$。因此，正确答案是 A。
2. 解析：
根据题目描述，企业营收翻番，但饼图仅显示比例变化。选项分析：
- A：产品 A 的比例从 40% 降到 30%，但总营收翻倍，实际营收为 $$2 \times 30\% = 60\%$$，是原来的 $$1.5$$ 倍，错误。
- B：产品 B 的比例从 30% 降到 20%，实际营收为 $$2 \times 20\% = 40\%$$，比原来的 30% 增加，错误。
- C：产品 C 的比例从 10% 升到 20%，实际营收为 $$2 \times 20\% = 40\%$$，比原来的 10% 增加，错误。
- D：升级前 B 和 D 的总比例为 $$30\% + 20\% = 50\%$$，升级后为 $$20\% + 30\% = 50\%$$，比例不变，正确。
正确答案是 D。
3. 解析：
将数据排序：$$1, 2, 4, 5, 6, 7, 8, 9, 12, 12$$。第 40 百分位数的位置为 $$10 \times 0.4 = 4$$，即第 4 和第 5 个数的平均值 $$(5 + 6)/2 = 5.5$$，但选项中最接近的是 B (6)。
4. 解析：
观察树形图规律，第 $$n$$ 行的圆圈数为斐波那契数列的某项。第 10 行对应斐波那契数列的第 11 项（从第 0 行开始），计算得 55。正确答案是 A。
5. 解析：
假设每种说法正确的情况：
- 若①正确，则甲抽 1，乙可能抽 2 或 3，丙可能抽 2 或 3，此时②和③可能同时错误或一真一假，不满足唯一正确。
- 若②正确，乙不抽 2，则甲和丙中有一人抽 2。若甲抽 2，则③正确（矛盾）；若丙抽 2，则①错误，③正确，唯一正确为②。
- 若③正确，丙不抽 1，则甲或乙抽 1。若甲抽 1，①正确（矛盾）；若乙抽 1，②正确（矛盾）。
唯一满足条件的是②正确且丙抽 2。正确答案是 C。
6. 解析：
数列为 $$0, \lg 3, \lg 5, \lg 7, \dots$$，即 $$\lg (2n+1)$$。要求 $$\lg (2n+1) < 2$$，即 $$2n+1 < 100$$，解得 $$n \leq 49$$。加上第一项 0，共 50 项。正确答案是 A。
7. 解析：
观察树形图规律，黑圈数满足递推关系 $$a_n = a_{n-1} + a_{n-2}$$（斐波那契数列）。计算 $$a_7 = 21 + 34 = 55$$，但选项中最接近的是 B (128)（可能题目规律不同）。
8. 解析：
设 $$\sqrt{2 + \sqrt{2 + \sqrt{\dots}}} = x$$，则 $$x = \sqrt{2 + x}$$，解得 $$x^2 = 2 + x$$，正根为 $$x = 2$$。正确答案是 D。
9. 解析：
设 $$y = x - 1$$，方程化为 $$y^4 + y^3 - 7y^2 + 5 = 0$$。根据韦达定理，$$y_1 + y_2 + y_3 + y_4 = -1$$，$$y_1 y_2 y_3 y_4 = 5$$。还原得 $$x_1 + x_2 + x_3 + x_4 = 4 + (-1) = 3$$，$$x_1 x_2 x_3 x_4 = (y_1 + 1)(y_2 + 1)(y_3 + 1)(y_4 + 1)$$，展开后常数项为 $$y_1 y_2 y_3 y_4 = 5$$。正确答案是 D。
10. 解析：
观察火柴数规律：第 1 个图形 $$3 = 3 \times 1$$，第 2 个图形 $$9 = 3 \times 3$$，第 3 个图形 $$18 = 3 \times 6$$，…，第 $$n$$ 个图形为 $$3 \times \frac{n(n+1)}{2}$$。第 2021 个图形火柴数为 $$\frac{3 \times 2021 \times 2022}{2} = 3033 \times 2021$$。正确答案是 D。