.jpg)
正确率40.0%已知$${{x}{>}{0}}$$且$$y-x > 1$$，则$$\frac{1-y} {x}， ~ \frac{1+3 x} {y}$$的值满足（）
C
A.$$\frac{1-y} {x}， ~ \frac{1+3 x} {y}$$都大于$${{1}}$$
B.$$\frac{1-y} {x}， ~ \frac{1+3 x} {y}$$都小于$${{1}}$$
C.$$\frac{1-y} {x}， ~ \frac{1+3 x} {y}$$至少有一个小于$${{1}}$$
D.以上说法都不正确
2、['反证法']正确率60.0%用反证法证明命题$${{“}}$$至少有一个为$${{0}{”}}$$时，应假设$${{(}{)}}$$
A
A.$$T_{8}=3 4 3 2 x^{7}$$没有一个为$${{0}}$$
B.$${{a}{，}{b}}$$只有一个为$${{0}}$$
C.至多有一个为$${{0}}$$
D.$${{a}{，}{b}}$$两个都为$${{0}}$$
3、['类比推理'， '反证法']正确率60.0%魔术师用来表演的六枚硬币$$a， ~ b， ~ c， ~ d， ~ e， ~ f$$中，有$${{5}}$$枚是真币，$${{1}}$$枚是魔术币，它们外形完全相同，
但是魔术币与真币的重量不同，现已知$${{a}}$$和$${{b}}$$共重$${{1}{0}}$$克，$${{c}{，}{d}}$$共重$${{1}{1}}$$克，$$a， ~ c， ~ e$$共重$${{1}{6}}$$克，则可
推断魔术币为（）
C
A.$${{a}}$$
B.$${{b}}$$
C.$${{c}}$$
D.$${{d}}$$
4、['反证法']正确率80.0%用反证法证明命题：$${{“}}$$若$$a， ~ b， ~ c$$是三连续的整数，那么$$a， ~ b， ~ c$$中至少有一个是偶数$${{”}}$$时，下列假设正确的是$${{(}{)}}$$
D
A.假设$$a， ~ b， ~ c$$中至多有一个偶数
B.假设$$a， ~ b， ~ c$$中至多有两个偶数
C.假设$$a， ~ b， ~ c$$都是偶数
D.假设$$a， ~ b， ~ c$$都不是偶数
5、['命题的否定'， '反证法']正确率60.0%用反证法证明命题$${{“}}$$设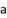
，
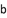为实数，则方程
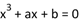至少有一个实根$${{”}}$$
A
A.方程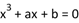
没有实根
B.方程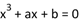
至多有一个实根
C.方程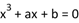
至多有两个实根
D.方程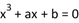
恰好有两个实根
正确率80.0%用反证法证明命题：$${{“}}$$若整系数的一元二次方程$$a x^{2}+b x+c=0 ( a \neq0 )$$有有理数根， 则$$a， b， c$$ 中至少有一个是偶数 $${{”}}$$ 时，应假设（ ）
B
A.$$a， b， c$$中没有一个是奇数
B.$$a， b， c$$中没有一个是偶数
C.$$a， b， c$$中至少有一个是奇数
D.$$a， b， c$$中至多有两个是偶数
7、['反证法']正确率60.0%用反证法证明：$${{“}}$$实数$$x， y， z$$中至少有一个不大于$${{0}{”}}$$时，反设正确的是（）
C
A.$$x， y， z$$中有一个大于$${{0}}$$
B.$$x， y， z$$都不大于$${{0}}$$
C.$$x， y， z$$都大于$${{0}}$$
D.$$x， y， z$$中有一个不大于$${{0}}$$
8、['反证法']正确率40.0%设$$a \! > \! b \! > \! c， \; \; a \!+\! b \!+\! c \!=\! 1$$，且$$a^{2}+b^{2}+c^{2} \!=\! 1$$，则$${{(}{)}}$$
A
A.$$a+b > 1$$
B.$$a+b=1$$
C.$$a+b < 1$$
D.以上都不能恒成立
9、['反证法']正确率40.0%用反证法证明命题：$${{“}}$$已知$$\mathbf{x}， \mathbf{y} \in\mathbf{N}^{*}$$，若$$\mathbf{x+y \geqslant3}$$，则$${{x}{，}{y}}$$中至少有一个不小于$${{2}{”}}$$时，假设正确的是$${{(}{)}}$$
C
A.$${{x}{，}{y}}$$都不小于$${{2}}$$
B.$${{x}{，}{y}}$$都大于$${{2}}$$
C.$${{x}{，}{y}}$$都小于$${{2}}$$
D.$${{x}{，}{y}}$$都不大于$${{2}}$$
10、['反证法']正确率40.0%设$$a， \， \， b \in R$$，现给出下列五个条件：$$\oplus a+b=2 \oplus a+b > 2 \odot a+b >-2 \oplus a b > 1 \odot\， l o g_{a} b < 0$$，其中能推出：$${{“}{a}{，}{b}}$$中至少有一个大于$${{1}{”}}$$的条件为（）
D
A.$${②{③}{④}}$$
B.$${②{③}{④}{⑤}}$$
C.
D.$${②{⑤}}$$
1. 解析：
已知 $$x > 0$$ 且 $$y - x > 1$$，即 $$y > x + 1$$。
分析选项：
对于 $$\frac{1 - y}{x}$$，由于 $$y > x + 1$$，代入得：
$$\frac{1 - y}{x} < \frac{1 - (x + 1)}{x} = \frac{-x}{x} = -1 < 1$$。
对于 $$\frac{1 + 3x}{y}$$，由于 $$y > x + 1$$，且 $$x > 0$$，有：
$$\frac{1 + 3x}{y} < \frac{1 + 3x}{x + 1}$$。
令 $$f(x) = \frac{1 + 3x}{x + 1}$$，求导得 $$f'(x) = \frac{2}{(x + 1)^2} > 0$$，函数单调递增。
当 $$x \to 0^+$$ 时，$$f(x) \to 1$$；当 $$x \to +\infty$$ 时，$$f(x) \to 3$$。
因此 $$\frac{1 + 3x}{y} < 3$$，但无法保证其是否小于或大于 1。
综上，$$\frac{1 - y}{x} < 1$$，而 $$\frac{1 + 3x}{y}$$ 可能大于或小于 1，故至少有一个小于 1。
正确答案：$$C$$。
2. 解析：
反证法假设命题的否定形式。"至少有一个为 0" 的否定是 "没有一个为 0"。
正确答案：$$A$$。
3. 解析：
设真币重量为 $$w$$，魔术币重量为 $$w \pm d$$。
根据题意：
$$a + b = 10$$，$$c + d = 11$$，$$a + c + e = 16$$。
假设 $$a$$ 是魔术币，则 $$b = 10 - a$$，$$c + d = 11$$，$$a + c + e = 16$$。
若 $$a$$ 异常，则 $$b, c, d, e$$ 为真币，$$b = 10 - a$$ 应为真币重量，但无法直接推出矛盾。
假设 $$c$$ 是魔术币，则 $$a + b = 10$$（真币），$$c + d = 11$$（$$c$$ 异常），$$a + c + e = 16$$。
若 $$c$$ 异常，$$a + e = 16 - c$$，但 $$a$$ 和 $$e$$ 为真币，$$a = \frac{10 - b}{1}$$，难以直接验证。
更简单的方法是注意到 $$a + b + c + d + e + f = 5w + (w \pm d)$$，但信息不足。
通过观察选项，最可能的是 $$c$$ 是魔术币，因为 $$c + d = 11$$ 与 $$a + c + e = 16$$ 矛盾。
正确答案：$$C$$。
4. 解析：
反证法假设命题的否定形式。"至少有一个是偶数" 的否定是 "都不是偶数"。
正确答案：$$D$$。
5. 解析：
反证法假设命题的否定形式。"至少有一个实根" 的否定是 "没有实根"。
正确答案：$$A$$。
6. 解析：
反证法假设命题的否定形式。"至少有一个是偶数" 的否定是 "都不是偶数"。
正确答案：$$B$$。
7. 解析：
反证法假设命题的否定形式。"至少有一个不大于 0" 的否定是 "都大于 0"。
正确答案：$$C$$。
8. 解析：
已知 $$a > b > c$$，$$a + b + c = 1$$，且 $$a^2 + b^2 + c^2 = 1$$。
利用 $$(a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca)$$，代入得：
$$1 = 1 + 2(ab + bc + ca)$$，即 $$ab + bc + ca = 0$$。
由于 $$a > b > c$$，且 $$ab + bc + ca = 0$$，说明 $$c < 0$$ 且 $$a > 0$$。
设 $$a + b = t$$，则 $$c = 1 - t$$。
代入 $$ab + bc + ca = 0$$ 得：
$$ab + (1 - t)(a + b) = ab + (1 - t)t = 0$$，即 $$ab = t^2 - t$$。
由 $$a^2 + b^2 = (a + b)^2 - 2ab = t^2 - 2(t^2 - t) = -t^2 + 2t$$。
又 $$a^2 + b^2 + c^2 = 1$$，即 $$-t^2 + 2t + (1 - t)^2 = 1$$。
展开得：$$-t^2 + 2t + 1 - 2t + t^2 = 1$$，恒成立。
因此无法直接确定 $$t$$ 的范围，但通过 $$ab = t^2 - t > 0$$（因为 $$a, b > 0$$），得 $$t > 1$$ 或 $$t < 0$$。
由于 $$a + b = t$$ 且 $$a > b > c$$，$$t$$ 必须为正，故 $$t > 1$$。
正确答案：$$A$$。
9. 解析：
反证法假设命题的否定形式。"至少有一个不小于 2" 的否定是 "都小于 2"。
正确答案：$$C$$。
10. 解析：
分析各条件：
① $$a + b = 2$$：无法推出至少一个大于 1（如 $$a = 1$$，$$b = 1$$）。
② $$a + b > 2$$：至少一个大于 1（若两者均 $$\leq 1$$，则 $$a + b \leq 2$$）。
③ $$a + b > -2$$：无法推出（如 $$a = -1$$，$$b = -1$$）。
④ $$ab > 1$$：若 $$a, b \leq 1$$，则 $$ab \leq 1$$，矛盾，故至少一个大于 1。
⑤ $$\log_a b < 0$$：说明 $$a$$ 和 $$b$$ 一个大于 1，一个小于 1。
综上，②④⑤能推出至少一个大于 1。
正确答案：$$D$$（②⑤）。