.jpg)
正确率60.0%用数学归纳法证明：$$( n+1 ) ( n+2 ) \ldots( n+n )$$$$= 2^{n} \times1 \times3 \times\ldots\times( 2 n-1 ) ( n \in{\bf N}^{*} )$$时，从$${{n}{=}{k}}$$到$$n=k+1，$$等式左边的变化是（）
C
A.增乘因式$$( 2 k+1 )$$
B.增乘因式$$( 2 k+1 )$$和$$( 2 k+2 )$$
C.增乘因式$$2 ( 2 k+1 )$$
D.增乘$$( 2 k+1 )$$同时除以$$( k+1 )$$
2、['数学归纳法的应用'， '*数学归纳法']正确率60.0%对于不等式$$\sqrt{n^{2}+n} < n+1 ( n \in\bf{N}_{+} )，$$某同学用数学归纳法的证明过程如下：
$${{(}{1}{)}}$$当$${{n}{=}{1}}$$时$$， ~ \sqrt{1^{2}+1} < ~ 1+1，$$不等式成立.
$${{(}{2}{)}}$$假设当$$n=k ( k \in\bf{N}_{+}， \ k \geq1 )$$时，不等式成立，即$$\sqrt{k^{2}+k} < k+1$$.当$$n=k+1$$时，$$\sqrt{( k+1 )^{2}+( k+1 )}=\sqrt{k^{2}+3 k+2} <$$$$\sqrt{( k^{2}+3 k+2 )+k+2}=\sqrt{( k+2 )^{2}}$$$$= ( k+1 )+1，$$
$${{∴}}$$当$$n=k+1$$时，不等式成立.
则上述证法（）
D
A.过程全部正确
B.$${{n}{=}{1}}$$验得不正确
C.归纳假设不正确
D.从$${{n}{=}{k}}$$到$$n=k+1$$的推理不正确
3、['数学归纳法的应用'， '函数的周期性'， '数列的通项公式']正确率40.0%若$${{a}_{1}{=}{1}}$$，对任意的$${{n}{∈}{{N}^{∗}}}$$，都有$${{a}_{n}{>}{0}}$$，且$$n a_{n+1}^{\， \， \， \， 2}-( 2 n-1 ) a_{n+1} a_{n}-2 a_{n}^{\， \， \， \， 2}=0$$，设$${{M}{(}{x}{)}}$$表示整数$${{x}}$$的个位数字，则$$M ( a_{2 \ 0 1 9} )=$$（）
B
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{8}}$$
4、['数学归纳法的应用']正确率80.0%用数学归纳法证明$$1+\frac1 2+\frac1 3+\ldots+\frac{1} {2 n-1} < n ( n \in\mathbf{N}^{*}， \ n > 1 ).$$第一步应验证不等式（）
B
A.$$1+\frac{1} {2} < 2$$
B.$$1+\frac1 2+\frac1 3 < 2$$
C.$$1+\frac1 2+\frac1 3 < 3$$
D.$$1+\frac{1} {2}+\frac{1} {3}+\frac{1} {4} < 3$$
5、['数学归纳法的应用']正确率60.0%用数学归纳法证明$$1+\frac1 2+\frac1 3+\ldots+\frac{1} {2^{n} \!-\! 1} \! < \! n \alpha\in N$$且$${{n}{>}{1}{）}}$$，第二步证明中从$${{“}{k}}$$到$${{k}{+}{1}{”}}$$时，左端增加的项数是（）
C
A.$${{2}^{k}{+}{1}}$$
B.$${{2}^{k}{−}{1}}$$
C.$${{2}^{k}}$$
D.$$2^{k-1}$$
6、['数学归纳法的应用'， '函数求解析式']正确率60.0%已知$$f \left( n \right)=\frac{1} {n+1}+\frac{1} {n+2}+\frac{1} {n+3}+\cdots+\frac{1} {3 n+1}$$，则$$f \left( k+1 \right)=\left( \begin{array} {l} {\mathbf{\Pi}} \\ \end{array} \right)$$
C
A.$$f \left( k \right)+\frac{1} {3 \left( k+1 \right)+1}$$
B.$$f \left( k \right)+\frac{2} {3 k+2}$$
C.$$f \left( k \right)+\frac{1} {3 k+2}+\frac{1} {3 k+3}+\frac{1} {3 k+4}-\frac{1} {k+1}$$
D.$$f \left( k \right)+\frac{1} {3 k+4}-\frac{1} {k+1}$$
7、['数学归纳法的应用']正确率60.0%用数学归纳法证明$$\frac{1} {1 \times2}+\frac{1} {2 \times3}+\cdots+\frac{1} {4 n \， ( 4 n+1 )} < 1 ( n \in N^{+}， n > 1 ) "$$< 1 (nin {N}^{+}，n >$${{1}{)}{”}}$$时，由$$n=k ( k > 1 )$$不等式成立，推证$$n=k+1$$时左边应增加的项数是（）
B
A.$${{1}}$$
B.$${{4}}$$
C.$${{k}}$$
D.$${{4}{k}}$$
8、['数学归纳法的应用']正确率40.0%下面四个判断中，正确的是$${{(}{)}}$$
C
A.$$f ( k )=1+k+k^{2}+\ldots+k^{n} ( n \in N^{*} )$$，当$${{n}{=}{1}}$$时，$${{f}{(}{k}{)}}$$恒为$${{1}}$$
B.$$f ( k )=1+k+k^{2}+\ldots+k^{n-1} ( n \in N^{*} )$$，当$${{n}{=}{1}}$$时，$${{f}{(}{k}{)}}$$恒为$${{1}{+}{k}}$$
C.$$f ( n )=1+\frac{1} {2}+\frac{1} {3}+\ldots+\frac{1} {2 n+1} ( n \in N^{*} )$$，当$${{n}{=}{1}}$$时，$${{f}{(}{n}{)}}$$为$$1+\frac{1} {2}+\frac{1} {3}$$
D.$$f ( n )=\frac{1} {n+1}+\frac{1} {n+2}+\ldots+\frac{1} {3 n+1} ( n \in N^{*} )$$，则$$f ( k+1 )=f ( k )+\frac{1} {3 k+2}+\frac{1} {3 k+3}+\frac{1} {3 k+4}$$
9、['数学归纳法的应用']正确率60.0%用数学归纳法证明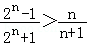
对任意$$n > k ( n， k \in N )$$
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['数学归纳法的应用']正确率40.0%用数学归纳法证明$$1-\frac1 2+\frac1 3-\frac1 4+\cdots-\frac1 n=2 \left( \frac1 {n+2}+\frac1 {n+4}+\cdots+\frac1 {2 n} \right) ( n$$为正偶数)时，若已假设$$n=k ( k \geq2$$且为正偶数)时命题为真，则还需要用归纳假设再证$${{(}{)}}$$
D
A.$$n=k+1$$时等式成立
B.$$n=2 \， ( k+2 )$$时等式成立
C.$$n=2 k+2$$时等式成立
D.$$n=k+2$$时等式成立
1. 解析：
2. 解析：
3. 解析：
4. 解析：
5. 解析：
6. 解析：
7. 解析：
8. 解析：
9. 解析：
10. 解析：