.jpg)
正确率80.0%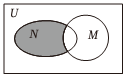
设全集$${{U}{=}{R}}$$，$$M=\{x | x^{2} > 4 \}， N=\{x | \frac{2} {x-1} \leqslant1 \}$$都是$${{U}}$$的子集，则图中阴影部分所表示的集合是$${{(}{)}}$$
A.$$\{x | x < 2 \}$$
B.$$\{x |-2 \leqslant x \leqslant2 \}$$
C.$$\{x | 1 < x \leqslant2 \}$$
D.$$\{x |-2 \leqslant x < 1 \}$$
2、['交集'， '不等式的解集与不等式组的解集']正确率60.0%已知集合$$A=\{x | x^{2}-x+4 > x+1 2 \}， \， \， \， B=\{x | 2^{x-1} < 8 \}$$，则
）
D
A.$$\{x | x \geqslant4 \}$$
B.$$\{x | x > 4 \}$$
C.$$\{x | x \geq-2 \}$$
D.$$\{x | x <-2 \}$$
3、['指数（型）函数的单调性'， '不等式的解集与不等式组的解集'， '集合的混合运算']正确率60.0%设集合$$M=\left\{x \right|-2 < x < 3 \}， \; \， N=\left\{x \vert2^{x+1} \leqslant1 \right\}$$，则$$M \bigcap( C_{R} N )=\c($$）
C
A.$$( 3，+\infty)$$
B.$$(-2，-1 ]$$
C.$$(-1， 3 )$$
D.$$[-1， 3 )$$
4、['不等式的解集与不等式组的解集'， '分段函数模型的应用']正确率40.0%已知函数$$f ( x )=\left\{\begin{matrix} {-3 x+3， x < 0} \\ {e^{-x}+1， x \geq0} \\ \end{matrix} \right.$$，则不等式$$f ( a ) < f ( 3 a-1 )$$的解集为$${{(}{)}}$$
A.$$( 0， \frac{1} {2} )$$
B.$$(-\frac{1} {2}， 0 )$$
C.$$(-\infty， \frac{1} {2} )$$
D.$$(-\infty，-\frac{1} {2} )$$
5、['不等式的解集与不等式组的解集'， '函数的对称性'， '函数单调性的应用']正确率60.0%已知定义域为$${{R}}$$的函数$${{f}{（}{x}{）}}$$满足$$f \left( \frac{} {3}-x \right) ~=f \left( \frac{} {x}+1 \right)$$，当$${{x}{⩾}{2}}$$时$${{f}{（}{x}{）}}$$单调递减且$$f \left( \begin{matrix} {a} \\ \end{matrix} \right) \ge f \left( \begin{matrix} {0} \\ \end{matrix} \right)$$，则实数$${{a}}$$的取值范围是（）
B
A.$$[ 2， ~+\infty)$$
B.$$[ 0， ~ 4 ]$$
C.$$( \mathrm{\mathbf{~-\infty， \ 0 ~}} )$$
D.$$( ~-\infty， ~ 0 ) ~ \cup[ 4， ~+\infty)$$
6、['不等式的解集与不等式组的解集'， '根据函数零点个数求参数范围'， '图象法']正确率19.999999999999996%函数$$y=k x+2$$与函数$$y=\frac{1} {| x |}$$的图象至少有两个公共点，关于$${{k}}$$不等式$$( k-2 ) a-k > 0$$有解，则实数$${{a}}$$的取值范围是$${{(}{)}}$$
B
A.$$- 1 < a < \frac{1} {3}$$
B.$$a < \frac{1} {3}$$
C.$${{a}{<}{−}{1}}$$
D.$${{a}{⩾}{1}}$$
7、['函数奇偶性的应用'， '不等式的解集与不等式组的解集'， '函数单调性的应用']正确率60.0%函数$$f ( x+1 )$$是$${{R}}$$上的奇函数，对任意实数$${{x}_{1}{，}{{x}_{2}}}$$都有$$( x_{1}-x_{2} ) [ f ( x_{1} )-f ( x_{2} ) ] < 0$$成立，则关于$${{x}}$$的不等式$$f ( 1-x ) < 0$$的解集是$${{(}{)}}$$
A
A.$$(-\infty， 0 )$$
B.$$( 0，+\infty)$$
C.$$(-\infty， 2 )$$
D.$$( 2，+\infty)$$
8、['一元二次方程的解集'， '不等式的解集与不等式组的解集'， '根据函数零点个数求参数范围'， '函数零点的概念'， '分段函数的图象']正确率40.0%已知函数$$f ( x )=\{\begin{array} {c} {\begin{array} {c} {x^{2}-3 x， x \geqslant0，} \\ \end{array}} \\ {-x^{2}+3 x， x < 0，} \\ \end{array}$$若函数$$g ( x )=3 [ f ( x ) ]^{2}+( m+3 ) f ( x )+m ( m \in R )$$恰有$${{6}}$$个不同的零点，则$${{m}}$$的取值范围为（$${）}$$．
D
A.$$( 0，+\infty)$$
B.$$( 0， 3 ) \cup( \frac{2 7} {4}，+\infty)$$
C.$$( 0， \frac{2 7} {4} )$$
D.$$( 0， 3 ) \cup( 3， \frac{2 7} {4} )$$
9、['一元二次不等式的解法'， '不等式的解集与不等式组的解集'， '二次函数的零点及其与对应方程的根、不等式解集之间的关系']正确率60.0%关于$${{x}}$$的不等式$$x^{2}+2 m x-1 5 m^{2} < 0 ~ ( m < 0 )$$的解集区间为$$( \ a， \ b )$$，且$$b-a=1 8$$，则$${{m}{=}{（}}$$）
D
A.$${{−}{2}}$$
B.$${{−}{1}}$$
C.$$- \frac{9} {2}$$
D.$$- \frac{9} {4}$$
10、['全集与补集'， '不等式的解集与不等式组的解集']正确率60.0%已知全集$$U=R， \， \， \， A=\{x | \frac{2 x-5} {x-1} \geq1 \}$$，则$${{C}_{R}{A}}$$等于$${{(}{)}}$$
A
A.$$\{x | 1 \leqslant x < 4 \}$$
B.$$\{x | 1 < x < 4 \}$$
C.$$\{x | x \leqslant4 \}$$
D.$$\{x | x < 4 \}$$
1. 首先解集合 $$M$$ 和 $$N$$：
$$M = \{x | x^2 > 4\} = \{x | x < -2 \text{ 或 } x > 2\}$$
解不等式 $$\frac{2}{x-1} \leq 1$$：
当 $$x-1 > 0$$ 时，$$2 \leq x-1 \Rightarrow x \geq 3$$
当 $$x-1 < 0$$ 时，$$2 \geq x-1 \Rightarrow x \leq 1$$（注意 $$x \neq 1$$）
因此 $$N = \{x | x \leq 1 \text{ 或 } x \geq 3\}$$
图中阴影部分表示 $$M \cap N$$ 的补集，即 $$\{x | -2 \leq x \leq 2\} \cap \{x | 1 < x < 3\}$$，结果为 $$\{x | 1 < x \leq 2\}$$，故选 C。
2. 解集合 $$A$$ 和 $$B$$：
$$A = \{x | x^2 - x + 4 > x + 12\} = \{x | x^2 - 2x - 8 > 0\} = \{x | x < -2 \text{ 或 } x > 4\}$$
$$B = \{x | 2^{x-1} < 8\} = \{x | x-1 < 3\} = \{x | x < 4\}$$
因此 $$A \cap B = \{x | x < -2\}$$，故选 D。
3. 解集合 $$N$$：
$$2^{x+1} \leq 1 \Rightarrow x+1 \leq 0 \Rightarrow x \leq -1$$，所以 $$N = \{x | x \leq -1\}$$
补集 $$C_R N = \{x | x > -1\}$$
与 $$M = \{x | -2 < x < 3\}$$ 的交集为 $$\{x | -1 < x < 3\}$$，故选 C。
4. 分情况讨论不等式 $$f(a) < f(3a-1)$$：
当 $$a < 0$$ 且 $$3a-1 < 0$$ 时：$$-3a + 3 < -9a + 6 \Rightarrow 6a < 3 \Rightarrow a < 0.5$$，与 $$a < 0$$ 结合得 $$a < 0$$
当 $$a \geq 0$$ 且 $$3a-1 \geq 0$$ 时：$$e^{-a} + 1 < e^{-3a+1} + 1 \Rightarrow -a < -3a + 1 \Rightarrow a < 0.5$$，与 $$a \geq 0$$ 结合得 $$0 \leq a < 0.5$$
综上，解集为 $$(-\infty, 0.5)$$，故选 C。
5. 由对称性 $$f\left(\frac{3}{2}\right)$$ 为极值点，函数在 $$x \geq 2$$ 单调递减，故 $$f(a) \geq f(0)$$ 等价于 $$a \leq 0$$ 或 $$a \geq 4$$，故选 D。
6. 联立方程 $$kx + 2 = \frac{1}{|x|}$$ 至少有两解，分析得 $$k < 0$$。不等式 $$(k-2)a - k > 0$$ 化为 $$a < \frac{k}{k-2}$$，因 $$k < 0$$，$$a$$ 需小于最小值 $$\frac{k}{k-2}$$ 的下界，即 $$a < -1$$，故选 C。
7. 由 $$f(x+1)$$ 为奇函数得 $$f(1) = 0$$，且 $$f(x)$$ 单调递减。不等式 $$f(1-x) < 0$$ 等价于 $$1-x > 1$$，即 $$x < 0$$，故选 A。
8. 设 $$t = f(x)$$，方程 $$3t^2 + (m+3)t + m = 0$$ 需有两正根且 $$t \neq 0$$。由判别式及根的条件得 $$m \in (0, 3) \cup \left(\frac{27}{4}, +\infty\right)$$，故选 B。
9. 不等式解为 $$(3m, -5m)$$，区间长度 $$-5m - 3m = -8m = 18$$，解得 $$m = -\frac{9}{4}$$，故选 D。
10. 解不等式 $$\frac{2x-5}{x-1} \geq 1$$：
当 $$x-1 > 0$$ 时：$$2x-5 \geq x-1 \Rightarrow x \geq 4$$
当 $$x-1 < 0$$ 时：$$2x-5 \leq x-1 \Rightarrow x \leq 4$$（注意 $$x \neq 1$$）
因此 $$A = \{x | x \leq 1 \text{ 或 } x \geq 4\}$$，补集 $$C_R A = \{x | 1 < x < 4\}$$，故选 B。