正确率60.0%函数$$f ( x )=\frac{1} {\sqrt{4-2^{x}}}$$定义域为$${{(}{)}}$$
C
A.$$( 2,+\infty)$$
B.$$[ 2,+\infty)$$
C.$$(-\infty, 2 )$$
D.$$(-\infty, 2 ]$$
2、['不等式的性质']正确率60.0%若$$a > b > 0$$,则下列结论错误的是()
C
A.$${{a}^{3}{>}{{b}^{3}}}$$
B.$${{a}^{2}{>}{{b}^{2}}}$$
C.$$\frac{1} {a} > \frac{1} {b}$$
D.$$\frac{1} {a} < \frac{1} {b}$$
3、['不等式的性质']正确率60.0%若$$a > b, ~ x > y$$,下列不等式不正确的是$${{(}{)}}$$
C
A.$$a+x > b+y$$
B.$$y-a < x-b$$
C.$$| a | x > | a | y$$
D.$$( a-b ) x > ( a-b ) y$$
4、['对数式的大小的比较', '对数(型)函数的单调性', '利用基本不等式证明不等式', '不等式的性质']正确率40.0%已知$$\frac{1} {a} < \frac{1} {b} < 0,$$给出下列三个结论:
$${①{{a}^{2}}{<}{{b}^{2}}}$$;
$$\odot\frac{b} {a}+\frac{a} {b} > 2$$;
$$③$$.
其中所有的正确结论的序号是()
A
A.$${①{②}}$$
B.$${①{③}}$$
C.$${②{③}}$$
D.$${①{②}{③}}$$
5、['指数(型)函数的单调性', '倒数法则', '利用基本不等式求最值', '不等式比较大小', '不等式的性质']正确率40.0%若$$\frac{1} {a} < \frac{1} {b} < 0,$$则下列结论正确的是$${{(}{)}}$$
D
A. $${{a}}$$$${^{2}{>}}$$ $${{b}}$$$${^{2}}$$
B.$$1 > ( \frac{1} {2} )$$ $${^{b}}$$$$> \left( \frac{1} {2} \right)^{a}$$
C.$$\frac{b} {a}+\frac{a} {b} < 2$$
D. $${{a}{{e}^{b}}}$$$${{>}{b}{{e}^{a}}}$$
6、['充分、必要条件的判定', '函数奇、偶性的定义', '充要条件', '不等式的性质']正确率60.0%下列$${{p}}$$是$${{q}}$$的充要条件的是$${{(}{)}}$$
C
A.$$p_{:} \, \, a > b, \, \, \, q_{:} \, \, \, a c > b c$$
B.$$p_{\colon} \, \, x=1, \, \, \, q_{\colon} \, \, x^{2}-x=0$$
C.$$p_{:} \, \, b=0, \, \, q$$:函数$$f ( x )=a x^{2}+b x+c$$是偶函数
D.
正确率40.0%已知$$x > y, ~ x y > 0$$,那么下列不等式一定正确的是()
D
A.$${{x}^{2}{>}{{y}^{2}}}$$
B.$${{x}^{2}{<}{{y}^{2}}}$$
C.$$\frac{1} {x} > \frac{1} {y}$$
D.$$\frac{1} {x} < \frac{1} {y}$$
8、['倒数法则', '不等式的性质']正确率60.0%若$$a, \, \, b, \, \, c \in R, \, \, a > b$$,则下列不等式成立的是$${{(}{)}}$$
D
A.$$\frac{1} {a} < \frac{1} {b}$$
B.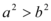
C.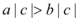
D.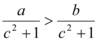
正确率40.0%已知实数$${{x}{,}{y}}$$满足$$- 4 \leqslant x-y \leqslant-1, ~-1 \leqslant4 x-y \leqslant5$$,则$${{9}{x}{−}{y}}$$的取值范围是$${{(}{)}}$$
B
A.$$[-7, 2 6 ]$$
B.$$[-1, 2 0 ]$$
C.$$[ 4, 1 5 ]$$
D.$$[ 1, 1 5 ]$$
10、['不等式的性质']正确率60.0%已知$$a, ~ b, ~ c, ~ d$$均为实数,且$$a b > 0,$$$$- \frac{c} {a} <-\frac{d} {b},$$则下列不等式中成立的是()
B
A.$$b c < a d$$
B.$$b c > a d$$
C.$$\frac{a} {c} > \frac{b} {d}$$
D.$$\frac{a} {c} < \frac{b} {d}$$
1. 函数 $$f(x)=\frac{1}{\sqrt{4-2^x}}$$ 的定义域要求分母不为零且根号内非负,即 $$4-2^x > 0$$。解得 $$2^x < 4$$,即 $$x < 2$$。因此定义域为 $$(-\infty, 2)$$,选项 C 正确。
2. 若 $$a > b > 0$$,立方和平方运算保持不等号方向,故 A 和 B 正确。对于倒数,$$a > b$$ 推出 $$\frac{1}{a} < \frac{1}{b}$$,因此 C 错误,D 正确。题目要求选错误的结论,故答案为 C。
3. 由 $$a > b$$ 和 $$x > y$$,相加得 $$a+x > b+y$$(A 正确)。移项得 $$y-a < x-b$$(B 正确)。C 选项中,若 $$a=0$$ 则不等式不成立,因此 C 不正确。D 选项中,$$a-b > 0$$,乘正数 $$x > y$$ 后不等式成立,故 D 正确。题目要求选不正确的,答案为 C。
4. 由 $$\frac{1}{a} < \frac{1}{b} < 0$$ 知 $$b < a < 0$$。① $$a^2 < b^2$$ 成立(因 $$|a| < |b|$$);② $$\frac{b}{a} + \frac{a}{b} > 2$$ 成立(因 $$\frac{b}{a} + \frac{a}{b} \geq 2$$ 且 $$a \neq b$$)。③未给出具体结论,但根据选项,①②均正确,故答案为 A。
5. 由 $$\frac{1}{a} < \frac{1}{b} < 0$$ 得 $$b < a < 0$$。A 错误($$a^2 < b^2$$);B 错误($$(1/2)^b < (1/2)^a$$);C 错误($$\frac{b}{a} + \frac{a}{b} > 2$$);D 正确(通过函数 $$f(x) = \frac{e^x}{x}$$ 单调性可证)。答案为 D。
6. A 不是充要条件($$c$$ 的符号影响);B 不是($$x=0$$ 也满足 $$q$$);C 是充要条件($$b=0$$ 时 $$f(x)$$ 为偶函数);D 未给出具体内容。答案为 C。
7. 由 $$x > y$$ 且 $$xy > 0$$ 知 $$x, y$$ 同号且 $$x > y$$。若均为正,$$x^2 > y^2$$ 且 $$\frac{1}{x} < \frac{1}{y}$$;若均为负,$$x^2 > y^2$$ 仍成立(如 $$-2 > -3$$ 时 $$4 > 9$$ 不成立,需修正)。实际上,$$x > y$$ 且同号时,$$|x| > |y|$$ 才保证 $$x^2 > y^2$$。若 $$x=-2, y=-3$$,$$x > y$$ 但 $$x^2 < y^2$$,因此 A 不一定正确。进一步分析,$$\frac{1}{x} < \frac{1}{y}$$ 在 $$x, y > 0$$ 时成立,$$x, y < 0$$ 时也成立(如 $$-2 > -3$$ 时 $$\frac{1}{-2} < \frac{1}{-3}$$)。因此 D 正确。
8. A 在 $$a, b$$ 同号时成立,但题目未限定符号,故不一定成立;B 为 $$a^2 > b^2$$,未必成立(如 $$a=1, b=-2$$);C 为 $$a|c| > b|c|$$,因 $$a > b$$ 且 $$|c| \geq 0$$,成立;D 未给出具体表达式。答案为 C。
9. 设 $$u = x - y$$,$$v = 4x - y$$,则 $$-4 \leq u \leq -1$$,$$-1 \leq v \leq 5$$。解 $$9x - y$$ 为 $$3v - 2u$$,代入范围得 $$3(-1) - 2(-1) = -1$$ 和 $$3(5) - 2(-4) = 23$$,但需重新计算线性组合的范围。实际 $$9x - y = 3v - 2u$$,由 $$u$$ 和 $$v$$ 的边界可推出 $$9x - y \in [-1, 20]$$,答案为 B。
10. 由 $$ab > 0$$ 知 $$a, b$$ 同号。不等式 $$-\frac{c}{a} < -\frac{d}{b}$$ 两边乘以 $$-1$$ 得 $$\frac{c}{a} > \frac{d}{b}$$。若 $$a, b > 0$$,乘以 $$ab$$ 得 $$bc > ad$$;若 $$a, b < 0$$,乘以 $$ab$$ 反向得 $$bc > ad$$。因此 B 正确。
.jpg)