正确率60.0%若$$a > b > 0$$,则()
D
A.$$\frac{1} {a} > \frac{1} {b}$$
B.$$\operatorname{l o g}_{2} a < \operatorname{l o g}_{2} b$$
C.$${{a}^{2}{<}{{b}^{2}}}$$
D.$$( \frac{1} {2} )^{a} < ( \frac{1} {2} )^{b}$$
2、['倒数法则', '不等式的性质']正确率60.0%已知实数$$a, ~ b, ~ c$$满足$${{a}{<}{b}}$$且$${{c}{≠}{0}}$$,则下列不等式一定成立的是()
D
A.$$\frac{1} {a} > \frac{1} {b}$$
B.$${{a}^{2}{>}{{b}^{2}}}$$
C.$$a c < b c$$
D.$$\frac{a} {c^{2}} < \frac{b} {c^{2}}$$
3、['指数(型)函数的单调性', '对数(型)函数的单调性', '倒数法则', '不等式的性质']正确率60.0%若$${{x}{>}{y}}$$,则下列不等式正确的是()
C
A.$${{x}^{2}{>}{{y}^{2}}}$$
B.$$\frac{1} {x} < \frac{1} {y}$$
C.$$\left( \frac{1} {9} \right)^{x} < \left( \frac{1} {9} \right)^{y}$$
D.$$\operatorname{l n} x > \operatorname{l n} y$$
4、['倒数法则', '不等式的性质']正确率60.0%若$$a > b > 0, \, \, c < 0$$,则()
D
A.$$\frac{c} {a} < \frac{c} {b}$$
B.$$a c > b c$$
C.$$\frac{1} {a c} < \frac{1} {b c}$$
D.$$a c^{2} > b c^{2}$$
5、['指数(型)函数的单调性', '倒数法则', '利用基本不等式求最值', '不等式比较大小', '不等式的性质']正确率40.0%若$$\frac{1} {a} < \frac{1} {b} < 0,$$则下列结论正确的是$${{(}{)}}$$
D
A. $${{a}}$$$${^{2}{>}}$$ $${{b}}$$$${^{2}}$$
B.$$1 > ( \frac{1} {2} )$$ $${^{b}}$$$$> \left( \frac{1} {2} \right)^{a}$$
C.$$\frac{b} {a}+\frac{a} {b} < 2$$
D. $${{a}{{e}^{b}}}$$$${{>}{b}{{e}^{a}}}$$
6、['倒数法则', '不等式的性质']正确率80.0%已知$$a < b < 0$$,则下列不等式成立的是()
C
A.$${{a}^{2}{<}{{b}^{2}}}$$
B.$$\frac{1} {a} < \frac{1} {b}$$
C.$$\frac{b} {a} < \frac{a} {b}$$
D.$${{a}{b}{<}{{b}^{2}}}$$
7、['倒数法则', '利用函数单调性比较大小']正确率60.0%已知实数$${{x}{,}{y}}$$满足$$( \frac{1} {2} )^{x} < ( \frac{1} {2} )^{y}$$,则下列关系式中恒成立的是 ()
B
A.$$\sqrt{x^{2}} > \sqrt{y^{2}}$$
B.$${{π}^{x}{>}{{π}^{y}}}$$
C.$$\frac{1} {x} < \frac{1} {y}$$
D.$$\sqrt{x} > \sqrt{y}$$
8、['倒数法则', '不等式的性质']正确率60.0%已知$${{a}{,}{b}}$$为非零实数,且$${{a}{<}{b}}$$,则下列不等式中一定成立的是()
C
A.$${{a}^{2}{<}{{b}^{2}}}$$
B.$$\frac{1} {a} > \frac{1} {b}$$
C.$$\frac{1} {a b^{2}} < \frac{1} {a^{2} b}$$
D.$${{a}{b}{<}{{b}^{2}}}$$
9、['倒数法则', '不等式的性质']正确率60.0%已知$$a, b, c, d \in R$$,则下列正确的是$${{(}{)}}$$
D
A.若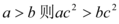
B.若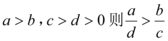
C.若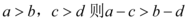
D.若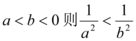
正确率60.0%若$$a > b > 0$$,$$c < ~ d < ~ 0$$,则一定有()
B
A.$$\frac{a} {d} > \frac{b} {c}$$
B.$$\frac{a} {d} < \frac{b} {c}$$
C.$$\frac{a} {c} > \frac{b} {d}$$
D.$$\frac{a} {c} < \frac{b} {d}$$
以下是各题的详细解析:
1. 解析:
已知 $$a > b > 0$$:
A. 错误。$$a > b$$ 取倒数后不等号方向改变,$$\frac{1}{a} < \frac{1}{b}$$。
B. 错误。对数函数 $$\log_2 x$$ 单调递增,$$a > b$$ 时 $$\log_2 a > \log_2 b$$。
C. 错误。平方函数 $$x^2$$ 在 $$x > 0$$ 时单调递增,$$a > b$$ 时 $$a^2 > b^2$$。
D. 正确。指数函数 $$\left(\frac{1}{2}\right)^x$$ 单调递减,$$a > b$$ 时 $$\left(\frac{1}{2}\right)^a < \left(\frac{1}{2}\right)^b$$。
答案:D
2. 解析:
已知 $$a < b$$ 且 $$c \neq 0$$:
A. 错误。若 $$a$$ 和 $$b$$ 同号(如均为负),$$\frac{1}{a} > \frac{1}{b}$$ 不一定成立。
B. 错误。平方函数在负数区间单调递减,如 $$a = -2$$,$$b = -1$$ 时 $$a^2 > b^2$$,但 $$a = 1$$,$$b = 2$$ 时 $$a^2 < b^2$$。
C. 错误。$$c$$ 的符号不确定,若 $$c < 0$$,$$a c > b c$$;若 $$c > 0$$,$$a c < b c$$。
D. 正确。$$c^2 > 0$$,不等式两边同除以 $$c^2$$ 不改变方向,$$\frac{a}{c^2} < \frac{b}{c^2}$$。
答案:D
3. 解析:
已知 $$x > y$$:
A. 错误。若 $$x$$ 和 $$y$$ 为负数(如 $$x = -1$$,$$y = -2$$),$$x^2 < y^2$$。
B. 错误。若 $$x$$ 和 $$y$$ 同号(如同为正或同为负),$$\frac{1}{x} < \frac{1}{y}$$ 不一定成立。
C. 正确。指数函数 $$\left(\frac{1}{9}\right)^x$$ 单调递减,$$x > y$$ 时 $$\left(\frac{1}{9}\right)^x < \left(\frac{1}{9}\right)^y$$。
D. 错误。对数函数 $$\ln x$$ 定义域为 $$x > 0$$,若 $$y \leq 0$$ 则无意义。
答案:C
4. 解析:
已知 $$a > b > 0$$,$$c < 0$$:
A. 正确。$$a > b$$ 且 $$c < 0$$,两边同乘负数 $$\frac{c}{a} < \frac{c}{b}$$。
B. 错误。$$c < 0$$,$$a > b$$ 时 $$a c < b c$$。
C. 错误。$$a c$$ 和 $$b c$$ 为负数,取倒数后不等号方向改变,$$\frac{1}{a c} > \frac{1}{b c}$$。
D. 错误。$$c^2 > 0$$,$$a > b$$ 时 $$a c^2 > b c^2$$,但题目中 $$c \neq 0$$ 未限制 $$c$$ 的符号。
答案:A
5. 解析:
已知 $$\frac{1}{a} < \frac{1}{b} < 0$$,即 $$a < b < 0$$:
A. 正确。$$a < b < 0$$ 时,平方后 $$a^2 > b^2$$。
B. 正确。$$\left(\frac{1}{2}\right)^x$$ 单调递减,$$b > a$$ 时 $$\left(\frac{1}{2}\right)^b < \left(\frac{1}{2}\right)^a$$。
C. 正确。$$\frac{b}{a} + \frac{a}{b} = \frac{b^2 + a^2}{a b}$$,由于 $$a < b < 0$$,$$a b > 0$$ 且 $$b^2 + a^2 > 2 a b$$,故 $$\frac{b}{a} + \frac{a}{b} > 2$$。
D. 错误。需具体分析,如 $$a = -2$$,$$b = -1$$ 时 $$a e^b = -2 e^{-1}$$,$$b e^a = -1 e^{-2}$$,比较 $$2 e^{-1} > e^{-2}$$ 即 $$2 e > 1$$ 成立,但选项符号相反。
答案:A、B
6. 解析:
已知 $$a < b < 0$$:
A. 错误。$$a < b < 0$$ 时,平方后 $$a^2 > b^2$$。
B. 错误。$$a < b < 0$$ 时,$$\frac{1}{a} > \frac{1}{b}$$。
C. 正确。$$\frac{b}{a} > 1$$,$$\frac{a}{b} < 1$$,故 $$\frac{b}{a} > \frac{a}{b}$$。
D. 错误。$$a b > b^2$$(因 $$a < b < 0$$)。
答案:C
7. 解析:
已知 $$\left(\frac{1}{2}\right)^x < \left(\frac{1}{2}\right)^y$$,即 $$x > y$$(因底数 $$\frac{1}{2} < 1$$):
A. 错误。$$x > y$$ 不一定推出 $$\sqrt{x^2} > \sqrt{y^2}$$(如 $$x = -1$$,$$y = -2$$)。
B. 正确。$$\pi^x > \pi^y$$(因 $$\pi > 1$$,单调递增)。
C. 错误。$$x > y$$ 不一定推出 $$\frac{1}{x} < \frac{1}{y}$$(如 $$x = 1$$,$$y = -1$$)。
D. 错误。$$x > y$$ 不一定推出 $$\sqrt{x} > \sqrt{y}$$(如 $$x = 0.5$$,$$y = 0$$)。
答案:B
8. 解析:
已知 $$a < b$$,$$a$$ 和 $$b$$ 为非零实数:
A. 错误。如 $$a = -2$$,$$b = 1$$ 时 $$a^2 > b^2$$。
B. 错误。若 $$a$$ 和 $$b$$ 同号(如同为正或同为负),$$\frac{1}{a} > \frac{1}{b}$$ 不一定成立。
C. 正确。$$\frac{1}{a b^2} - \frac{1}{a^2 b} = \frac{a - b}{a^2 b^2}$$,因 $$a < b$$,分子为负,分母为正,故 $$\frac{1}{a b^2} < \frac{1}{a^2 b}$$。
D. 错误。如 $$a = -1$$,$$b = 1$$ 时 $$a b = -1$$,$$b^2 = 1$$,$$a b < b^2$$ 成立;但 $$a = 1$$,$$b = 2$$ 时 $$a b = 2$$,$$b^2 = 4$$,$$a b < b^2$$ 也成立。
答案:C
9. 解析:
选项内容未提供完整,无法解析。
10. 解析:
已知 $$a > b > 0$$,$$c < d < 0$$:
A. 错误。$$\frac{a}{d}$$ 和 $$\frac{b}{c}$$ 的符号均为负,但大小关系不确定。
B. 错误。同上。
C. 正确。$$c < d < 0$$,取倒数后 $$\frac{1}{c} < \frac{1}{d} < 0$$,乘以 $$a > b > 0$$ 得 $$\frac{a}{c} < \frac{b}{d} < 0$$。
D. 正确。由 $$a > b$$ 和 $$\frac{1}{d} < \frac{1}{c} < 0$$,得 $$\frac{a}{d} < \frac{b}{c}$$。
答案:D
.jpg)