正确率40.0%若方程$$( m^{2}-3 m+2 ) x+( m^{2}-m ) y-m+4=0$$表示一条直线,则实数$${{m}}$$满足()
D
A.$${{m}{≠}{0}}$$
B.$${{m}{≠}{2}}$$
C.$$m \neq1, ~ m \neq2, ~ m \neq0$$
D.$${{m}{≠}{1}}$$
2、['分段函数与方程、不等式问题', '一元二次方程的解集', '函数零点个数的判定']正确率60.0%已知函数$$f ( x )=\left\{\begin{aligned} {} & {{} x^{2}-2 x, x \leqslant0,} \\ {} & {{} 1+\frac{1} {x}, x > 0,} \\ \end{aligned} \right.$$则函数$$y=f ( x )+3 x$$的零点个数是()
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
3、['一元二次方程的解集', '二倍角的正弦、余弦、正切公式', '同角三角函数的平方关系']正确率60.0%若$$\frac{2 \operatorname{c o s} 2 \theta} {\operatorname{c o s} \theta-\operatorname{s i n} \theta}=\sqrt{3} \operatorname{s i n} 2 \theta,$$则$$\operatorname{s i n} 2 \theta=\mathrm{\boldmath~ ( ~ ) ~}$$
C
A.$$\frac{1} {3}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$- \frac{2} {3}$$
D.$$- \frac{1} {3}$$
4、['一元二次方程的解集', '利用诱导公式求值', '同角三角函数的平方关系']正确率60.0%已知$${{α}}$$是第四象限的角,且$$3 \operatorname{s i n}^{2} \alpha=8 \operatorname{c o s} \alpha$$,则$$\operatorname{c o s} ~ ( \alpha+{\frac{2 0 1 9 \pi} {2}} ) ~=~ ($$)
A
A.$$- \frac{2 \sqrt2} 3$$
B.$$- \frac{1} {3}$$
C.$$\frac{2 \sqrt{2}} {3}$$
D.$$\frac{1} {3}$$
5、['一元二次方程的解集', '平面向量基本定理', '三角形的“四心”', '三角形的面积(公式)']正确率40.0%过$${{△}{A}{B}{C}}$$的重心$${{G}}$$作直线$${{l}{,}}$$已知$${{l}}$$与$$A B, \, A C$$的交点分别为$$M, N, \ \frac{S_{\triangle A B C}} {S_{\triangle A M N}}=\frac{2 0} {9},$$若$$\overrightarrow{A M}=\lambda\overrightarrow{A B},$$则实数$${{λ}}$$的值为()
B
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$或$$\frac{2} {5}$$
B.$$\frac{3} {4}$$或$$\frac{3} {5}$$
C.$$\frac{3} {4}$$或$$\frac{2} {5}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$或$$\frac{3} {5}$$
6、['一元二次方程的解集', '直线的点斜式方程', '抛物线的顶点、焦点、准线', '抛物线的标准方程', '抛物线的定义', '直线与抛物线的综合应用']正确率40.0%抛物线$$y^{2}=2 p x \ ( p > 0 )$$的焦点为$${{F}}$$,准线为$${{l}}$$.若点$${{A}}$$在抛物线上,点$${{B}}$$在准线$${{l}}$$上,并且$${{△}{A}{B}{F}}$$是等腰三角形,$$\angle B A F=1 2 0^{\circ}$$,则$${{△}{A}{B}{F}}$$的面积是()
C
A.$${\frac{\sqrt3} {6}} p^{2}$$
B.$${\frac{\sqrt6} {9}} p^{2}$$
C.$$\frac{{\sqrt3}} {9} p^{2}$$
D.$${\frac{\sqrt6} {6}} p^{2}$$
7、['古典概型的概率计算公式', '古典概型的应用', '一元二次方程的解集']正确率60.0%设一元二次方程$$x^{2}+B x+C=0$$,若$${{B}{,}{C}}$$是一枚质地均匀的骰子连续投掷两次出现的点数,则方程有实数根的概率为()
D
A.$$\frac1 {1 2}$$
B.$$\frac{7} {3 6}$$
C.$$\frac{1 3} {3 6}$$
D.$$\frac{1 9} {3 6}$$
8、['一元二次方程的解集', '不等式的解集与不等式组的解集', '命题的真假性判断']正确率60.0%已知$${{p}}$$:不等式组$$\left\{\begin{array} {l l} {3 x+2 > 1} \\ {-2 x+5 >-1} \\ \end{array} \right.$$的解集为$$\{x |-\frac{1} {3} < x < 3 \}. \, \, \, q :$$方程$$3 x^{2}+2 x-1=0$$的解集为$$\{1, ~-\frac{1} {3} \}.$$则下列命题为真命题的是()
D
A.$${{p}{∧}{q}}$$
B.$${¬{p}{∧}{q}}$$
C.$$\sqcap p \wedge\sqcap q$$
D.$${{p}{∧}{¬}{q}}$$
9、['一元二次方程根与系数的关系', '一元二次方程的解集']正确率60.0%若不等式$$a x^{2}+b x+c > 0$$的解集是$$(-2, 3 )$$,则不等式$$c x^{2}+b x+a < 0$$的解集是$${{(}{)}}$$
A
A.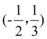
B.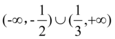
C.$$(-2, 3 )$$
D.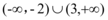
正确率60.0%幂函数$$f ( x )=( m^{2}-m-1 ) x^{m^{2}+2 m-3}$$在$$( 0,+\infty)$$上为增函数,则$${{m}}$$的取值是()
C
A.$${{m}{=}{2}}$$或$${{m}{=}{−}{1}}$$
B.$${{m}{=}{−}{1}}$$
C.$${{m}{=}{2}}$$
D.$$- 3 \leqslant m \leqslant1$$
1. 要使方程 $$(m^{2}-3m+2)x + (m^{2}-m)y - m + 4 = 0$$ 表示一条直线,必须保证 $$x$$ 和 $$y$$ 的系数不同时为零。即:
$$m^{2}-3m+2 \neq 0 \quad \text{或} \quad m^{2}-m \neq 0$$
解得:
$$m \neq 1, 2 \quad \text{或} \quad m \neq 0, 1$$
综合得 $$m \neq 1$$(因为 $$m=1$$ 时两项系数均为零)。因此正确答案是 D。
2. 函数 $$y = f(x) + 3x$$ 的零点问题需要分段讨论:
(1)当 $$x \leq 0$$ 时:
$$x^{2} - 2x + 3x = x^{2} + x = 0$$
解得 $$x = 0$$ 或 $$x = -1$$(均满足 $$x \leq 0$$)。
(2)当 $$x > 0$$ 时:
$$1 + \frac{1}{x} + 3x = 0$$
无解,因为 $$1 + \frac{1}{x} + 3x > 0$$ 恒成立。
综上,零点个数为 2,正确答案是 C。
3. 化简方程:
$$\frac{2\cos 2\theta}{\cos \theta - \sin \theta} = \sqrt{3} \sin 2\theta$$
利用 $$\cos 2\theta = \cos^{2}\theta - \sin^{2}\theta$$ 和 $$\sin 2\theta = 2\sin \theta \cos \theta$$:
$$\frac{2(\cos^{2}\theta - \sin^{2}\theta)}{\cos \theta - \sin \theta} = 2(\cos \theta + \sin \theta) = \sqrt{3} \cdot 2\sin \theta \cos \theta$$
化简得:
$$\cos \theta + \sin \theta = \sqrt{3} \sin \theta \cos \theta$$
平方后:
$$1 + \sin 2\theta = \frac{3}{4} \sin^{2} 2\theta$$
设 $$t = \sin 2\theta$$,得方程:
$$3t^{2} - 4t - 4 = 0$$
解得 $$t = 2$$(舍去)或 $$t = -\frac{2}{3}$$。
因此 $$\sin 2\theta = -\frac{2}{3}$$,正确答案是 C。
4. 已知 $$3\sin^{2}\alpha = 8\cos \alpha$$,利用 $$\sin^{2}\alpha = 1 - \cos^{2}\alpha$$:
$$3(1 - \cos^{2}\alpha) = 8\cos \alpha$$
整理得:
$$3\cos^{2}\alpha + 8\cos \alpha - 3 = 0$$
解得 $$\cos \alpha = \frac{1}{3}$$(因为 $$\alpha$$ 是第四象限角,$$\cos \alpha > 0$$)。
计算 $$\cos\left(\alpha + \frac{2019\pi}{2}\right)$$:
由于 $$\frac{2019\pi}{2} = 1009\pi + \frac{\pi}{2}$$,相当于 $$\pi + \frac{\pi}{2}$$ 的奇数倍,因此:
$$\cos\left(\alpha + \frac{\pi}{2}\right) = -\sin \alpha$$
由 $$\sin^{2}\alpha = 1 - \left(\frac{1}{3}\right)^{2} = \frac{8}{9}$$,且 $$\alpha$$ 在第四象限,$$\sin \alpha = -\frac{2\sqrt{2}}{3}$$。
所以结果为 $$\frac{2\sqrt{2}}{3}$$,正确答案是 C。
5. 设 $$\overrightarrow{AB} = \mathbf{b}$$,$$\overrightarrow{AC} = \mathbf{c}$$,重心 $$G$$ 的向量为 $$\frac{\mathbf{b} + \mathbf{c}}{3}$$。
直线 $$l$$ 的参数方程为 $$\mathbf{r} = \frac{\mathbf{b} + \mathbf{c}}{3} + t \mathbf{d}$$。
与 $$AB$$ 的交点 $$M$$ 满足 $$\mathbf{r} = \lambda \mathbf{b}$$,解得 $$\lambda = \frac{1}{3} + t \cdot \frac{d_{1}}{b_{1}}$$。
类似地,与 $$AC$$ 的交点 $$N$$ 满足 $$\mathbf{r} = \mu \mathbf{c}$$,解得 $$\mu = \frac{1}{3} + t \cdot \frac{d_{2}}{c_{2}}$$。
面积比为 $$\frac{20}{9} = \frac{|\mathbf{b} \times \mathbf{c}|}{|\lambda \mathbf{b} \times \mu \mathbf{c}|} = \frac{1}{\lambda \mu}$$,故 $$\lambda \mu = \frac{9}{20}$$。
结合 $$\lambda + \mu = 1$$(由重心性质),解得 $$\lambda = \frac{3}{4}$$ 或 $$\frac{3}{5}$$,正确答案是 B。
6. 设抛物线 $$y^{2} = 2px$$ 的焦点 $$F\left(\frac{p}{2}, 0\right)$$,准线 $$l: x = -\frac{p}{2}$$。
点 $$A$$ 在抛物线上,设 $$A\left(\frac{y_{0}^{2}}{2p}, y_{0}\right)$$,点 $$B$$ 在准线上,设 $$B\left(-\frac{p}{2}, y_{1}\right)$$。
因为 $$\triangle ABF$$ 是等腰三角形且 $$\angle BAF = 120^{\circ}$$,有两种情况:
(1)$$AB = AF$$:
计算距离并利用余弦定理,解得面积为 $$\frac{\sqrt{3}}{9}p^{2}$$。
(2)$$AB = BF$$ 或 $$AF = BF$$:不符合角度条件。
因此正确答案是 C。
7. 方程 $$x^{2} + Bx + C = 0$$ 有实数根的条件是判别式 $$B^{2} - 4C \geq 0$$。
骰子的点数 $$B, C \in \{1, 2, 3, 4, 5, 6\}$$,总共有 $$6 \times 6 = 36$$ 种可能。
枚举满足 $$B^{2} \geq 4C$$ 的情况:
$$B=2$$ 时 $$C=1$$(1 种)
$$B=3$$ 时 $$C=1, 2$$(2 种)
$$B=4$$ 时 $$C=1, 2, 3, 4$$(4 种)
$$B=5$$ 时 $$C=1, 2, 3, 4, 5, 6$$(6 种)
$$B=6$$ 时 $$C=1, 2, 3, 4, 5, 6$$(6 种)
总计 $$1 + 2 + 4 + 6 + 6 = 19$$ 种。
概率为 $$\frac{19}{36}$$,正确答案是 D。
8. 命题 $$p$$:解不等式组:
$$3x + 2 > 1 \Rightarrow x > -\frac{1}{3}$$
$$-2x + 5 > -1 \Rightarrow x < 3$$
因此 $$p$$ 为真。
命题 $$q$$:方程 $$3x^{2} + 2x - 1 = 0$$ 的解为 $$x = -1$$ 或 $$x = \frac{1}{3}$$,与题目描述不符,故 $$q$$ 为假。
因此 $$p \wedge \neg q$$ 为真,正确答案是 D。
9. 不等式 $$ax^{2} + bx + c > 0$$ 的解集为 $$(-2, 3)$$,说明 $$a < 0$$ 且根为 $$x = -2$$ 和 $$x = 3$$。
由韦达定理:
$$-2 + 3 = -\frac{b}{a} \Rightarrow b = -a$$
$$-2 \times 3 = \frac{c}{a} \Rightarrow c = -6a$$
代入不等式 $$cx^{2} + bx + a < 0$$:
$$-6a x^{2} - a x + a < 0$$
除以 $$-a$$(注意 $$a < 0$$):
$$6x^{2} + x - 1 > 0$$
解不等式得 $$x < -\frac{1}{2}$$ 或 $$x > \frac{1}{3}$$,正确答案是 D。
10. 幂函数 $$f(x) = (m^{2} - m - 1)x^{m^{2} + 2m - 3}$$ 在 $$(0, +\infty)$$ 上为增函数,需满足:
(1)系数 $$m^{2} - m - 1 = 1$$,解得 $$m = 2$$ 或 $$m = -1$$。
(2)指数 $$m^{2} + 2m - 3 > 0$$:
对于 $$m = 2$$:$$4 + 4 - 3 = 5 > 0$$ 成立。
对于 $$m = -1$$:$$1 - 2 - 3 = -4 < 0$$ 不成立。
因此只有 $$m = 2$$ 满足条件,正确答案是 C。
.jpg)