正确率60.0%指数函数$$y=\left( \frac{b} {a} \right)^{x}$$的图象如图所示,其中$$A (-1, ~ 2 ), ~ B \left( 1, ~ \frac{1} {3} \right),$$则二次函数$$y=b x^{2}-a x$$的图象的顶点的横坐标的取值范围是()
B
A.$$\left( \frac{1} {6}, \, \frac{1} {4} \right)$$
B.$$\left( 1, ~ \frac{3} {2} \right)$$
C.$$( 2, \ 3 )$$
D.$$( 3, ~+\infty)$$
2、['函数图象的识别', '二次函数的图象分析与判断']正确率60.0%如图,某小区内有一个矩形花坛$$A B C D,$$已知矩形$${{A}{B}{C}{D}}$$的周长是$${{4}{,}}$$设$$A B=x, \, \, \, A C=y,$$则函数$$y=f ( x )$$的大致图象为()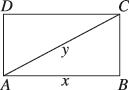
C
A.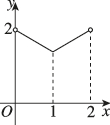
B.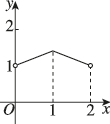
C.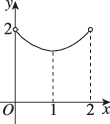
D.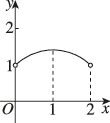
正确率60.0%在同一平面直角坐标系中,二次函数$$y=a x^{2}+b x ( x \neq0 )$$与幂函数$$y=x^{\frac{b} {a}} ( x > 0 )$$的图象可能为()
A
A.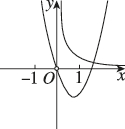
B.
C.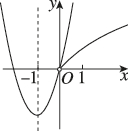
D.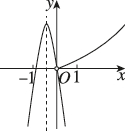
正确率40.0%如图所示,半圆的直径$${{A}{B}}$$=$${{2}}$$,$${{O}}$$为圆心,$${{C}}$$是半圆上不同于$${{A}}$$,$${{B}}$$的任意一点,若$${{P}}$$为半径$${{O}{C}}$$上的动点,则$$( \overrightarrow{P A}+\overrightarrow{P B} ) \cdot\overrightarrow{P C}$$的最小值是()
C
A.$$\frac{1} {2}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$- \frac{1} {2}$$
D.$$\frac{1} {4}$$
5、['向量的模', '向量的数量积的定义', '二次函数的图象分析与判断']正确率40.0%已知两个单位向量$${{a}^{→}}$$ ,$${{b}^{→}}$$的夹角为$${{1}{2}{0}^{∘}}$$,$${{k}{∈}{R}}$$,则$$\left| \overrightarrow{a}-k \overrightarrow{b} \right|$$的最小值为()
B
A.$$\frac{3} {4}$$
B.$$\frac{\sqrt3} {2}$$
C.$${{1}}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
6、['函数图象的识别', '二次函数的图象分析与判断', '反比例函数模型的应用']正确率60.0%二次函数$$y=a x^{2}+b x$$和反比例函数$$y=\frac{b} {x}$$在同一坐标系中的图象可能是()
B
A.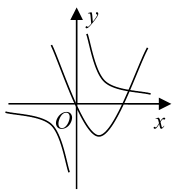
B.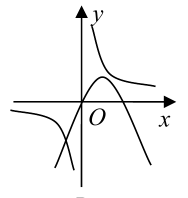
C.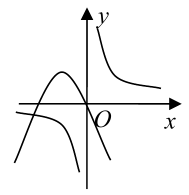
D.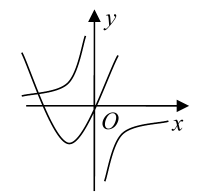
正确率60.0%函数$$y=\textsub( \frac1 {1 0} ) \rq{}^{2 x-x^{2}}$$的单调递增区间为()
D
A.$$(-\infty, \ 1 ]$$
B.$$(-\infty, \ 2 ]$$
C.$$[ 2, ~+\infty)$$
D.$$[ 1, ~+\infty)$$
8、['利用函数单调性求参数的取值范围', '二次函数的图象分析与判断']正确率60.0%如果函数$$f \left( x \right)=x^{2}-a x-3$$在区间$$(-\infty, 4 ]$$上单调递减,那么实数$${{a}}$$的取值范围是()
A
A.$${{a}{⩾}{8}}$$
B.$${{a}{⩽}{8}}$$
C.$${{a}{⩾}{4}}$$
D.$${{a}{⩽}{4}}$$
9、['二次函数的图象分析与判断']正确率60.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=-x^{2}+b x+c$$,且$$f \left( \textbf{x}+1 \right)$$是偶函数,则$$f ~ ( \textit{}-{\bf1} ) ~, ~ f ~ ( {\bf1} ) ~, ~ f ~ ( {\bf2} )$$的大小关系是()
D
A.$$f ~ ( \mathrm{\Theta~ ( \it-1 ) ~} < f ~ ( \mathrm{\O~ 1} ) ~ < f ~ ( \mathrm{\Theta~ 2} )$$
B.$$f \ ( \textbf{1} ) \ < f \ ( \textbf{2} ) \ < f \ ( \textbf{-1} )$$
C.$$f ~ ( \mathbf{2} ) ~ < f ~ ( \mathbf{\Omega}-\mathbf{1} ) ~ < f ~ ( \mathbf{1} )$$
D.$$f ~ ( \textit{-1} ) ~ < f ~ ( \textit{2} ) ~ < f ~ ( \textit{1} )$$
10、['导数中不等式恒成立与存在性问题', '二次函数的图象分析与判断']正确率40.0%已知函数$$y=~ ( \ensuremath{x}^{2}+b \ensuremath{x}-4 ) ~ l o g_{a} x ~ ( \ensuremath{a} > 0$$且$${{a}{≠}{1}{)}}$$若对任意$${{x}{>}{0}}$$,恒有$${{y}{⩽}{0}}$$,则$${{b}^{a}}$$的取值范围是()
B
A.$$( {\bf0}, \mathrm{\bf~ 3} )$$
B.$$( 1, \ 3 )$$
C.$$( \mathbf{3}, \mathbf{\Lambda}+\infty)$$
D.$$( \ 2, \ 4 )$$
1. 解析:
由指数函数$$y=\left( \frac{b}{a} \right)^x$$的图象经过点$$A(-1, 2)$$和$$B\left(1, \frac{1}{3}\right)$$,可以得到:
$$2 = \left( \frac{b}{a} \right)^{-1} \Rightarrow \frac{a}{b} = 2 \Rightarrow a = 2b$$
$$\frac{1}{3} = \left( \frac{b}{a} \right)^1 \Rightarrow \frac{b}{a} = \frac{1}{3} \Rightarrow a = 3b$$
联立解得$$a = 6$$,$$b = 2$$。
二次函数$$y = bx^2 - ax = 2x^2 - 6x$$的顶点横坐标为$$x = \frac{a}{2b} = \frac{6}{4} = \frac{3}{2}$$。
因此,顶点的横坐标在选项B的范围内$$\left(1, \frac{3}{2}\right)$$。
答案:B
2. 解析:
矩形$$ABCD$$的周长为4,设$$AB = x$$,则$$BC = 2 - x$$。
对角线$$AC = y = \sqrt{x^2 + (2 - x)^2} = \sqrt{2x^2 - 4x + 4}$$。
化简得$$y = \sqrt{2(x - 1)^2 + 2}$$,其图象为开口向上的抛物线,对称轴为$$x = 1$$。
观察选项,只有选项D符合函数$$y = f(x)$$的图象特征。
答案:D
3. 解析:
二次函数$$y = ax^2 + bx$$的图象开口方向由$$a$$决定,幂函数$$y = x^{\frac{b}{a}}$$的性质由$$\frac{b}{a}$$决定。
选项A中,二次函数开口向上($$a > 0$$),幂函数为减函数($$\frac{b}{a} < 0$$),符合逻辑。
选项B、C、D中,二次函数与幂函数的性质矛盾,排除。
答案:A
4. 解析:
设半圆的半径为1,$$P$$在$$OC$$上,设$$OP = t$$($$0 \leq t \leq 1$$)。
向量$$\overrightarrow{PA} + \overrightarrow{PB} = 2\overrightarrow{PO}$$,因此:
$$( \overrightarrow{PA} + \overrightarrow{PB} ) \cdot \overrightarrow{PC} = 2\overrightarrow{PO} \cdot \overrightarrow{PC} = 2\overrightarrow{PO} \cdot (\overrightarrow{PO} + \overrightarrow{OC}) = 2|\overrightarrow{PO}|^2 + 2\overrightarrow{PO} \cdot \overrightarrow{OC}$$。
由于$$\overrightarrow{PO} = -t\overrightarrow{OC}$$,代入得:
$$2t^2 + 2(-t)(1) = 2t^2 - 2t$$。
求最小值时,对$$f(t) = 2t^2 - 2t$$求导,$$f'(t) = 4t - 2$$,令导数为0得$$t = \frac{1}{2}$$。
代入得最小值为$$2 \times \left(\frac{1}{2}\right)^2 - 2 \times \frac{1}{2} = -\frac{1}{2}$$。
答案:C
5. 解析:
单位向量$$|\overrightarrow{a}| = |\overrightarrow{b}| = 1$$,夹角为$$120^\circ$$。
$$|\overrightarrow{a} - k\overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + k^2|\overrightarrow{b}|^2 - 2k\overrightarrow{a} \cdot \overrightarrow{b} = 1 + k^2 - 2k \times \left(-\frac{1}{2}\right) = k^2 + k + 1$$。
对$$f(k) = k^2 + k + 1$$求最小值,导数为$$f'(k) = 2k + 1$$,令导数为0得$$k = -\frac{1}{2}$$。
代入得最小值为$$\left(-\frac{1}{2}\right)^2 + \left(-\frac{1}{2}\right) + 1 = \frac{3}{4}$$。
答案:A
6. 解析:
二次函数$$y = ax^2 + bx$$的图象过原点,反比例函数$$y = \frac{b}{x}$$的图象在$$b > 0$$时位于一、三象限,$$b < 0$$时位于二、四象限。
选项A中,二次函数开口向上($$a > 0$$),反比例函数位于一、三象限($$b > 0$$),且二次函数对称轴在$$x = -\frac{b}{2a} < 0$$,符合逻辑。
其他选项不符合二次函数与反比例函数的性质。
答案:A
7. 解析:
函数$$y = \left(\frac{1}{10}\right)^{2x - x^2}$$的底数为$$\frac{1}{10} < 1$$,因此函数单调性与指数部分$$2x - x^2$$相反。
$$2x - x^2$$的单调递减区间为$$[1, +\infty)$$,因此$$y$$的单调递增区间为$$[1, +\infty)$$。
答案:D
8. 解析:
函数$$f(x) = x^2 - ax - 3$$的对称轴为$$x = \frac{a}{2}$$。
在区间$$(-\infty, 4]$$上单调递减,需满足$$\frac{a}{2} \geq 4$$,即$$a \geq 8$$。
答案:A
9. 解析:
$$f(x+1)$$是偶函数,说明$$f(x)$$关于$$x = 1$$对称,即$$f(x) = f(2 - x)$$。
代入$$f(x) = -x^2 + bx + c$$,比较系数可得$$b = 4$$。
因此$$f(x) = -x^2 + 4x + c$$,其图象开口向下,对称轴为$$x = 2$$。
比较函数值:$$f(-1) = -1 - 4 + c = c - 5$$,$$f(1) = -1 + 4 + c = c + 3$$,$$f(2) = -4 + 8 + c = c + 4$$。
显然$$f(-1) < f(1) < f(2)$$。
答案:A
10. 解析:
对任意$$x > 0$$,$$y = (x^2 + bx - 4)\log_a x \leq 0$$,需分两种情况:
(1)若$$a > 1$$,$$\log_a x$$在$$x > 1$$时为正,$$x^2 + bx - 4 \leq 0$$需成立,但不可能对所有$$x > 0$$成立。
(2)若$$0 < a < 1$$,$$\log_a x$$在$$x > 1$$时为负,$$x^2 + bx - 4 \geq 0$$需成立。
要求$$x^2 + bx - 4 \geq 0$$对所有$$x > 0$$成立,需判别式$$\Delta = b^2 + 16 \leq 0$$,不可能。
进一步分析,只需$$x^2 + bx - 4$$在$$x = 1$$处为零且导数非负:
$$1 + b - 4 = 0 \Rightarrow b = 3$$,且$$2x + b \geq 0$$在$$x = 1$$时成立。
因此$$b = 3$$,$$0 < a < 1$$,$$b^a$$的取值范围为$$(1, 3)$$。
答案:B
.jpg)