正确率80.0%已知全集$${{U}{=}{R}}$$,能表示集合$$A=\{x \in N | x^{2}-3 x \leqslant0 \}$$与$$B=\{1, 2 \}$$关系的$${{V}{e}{n}{n}}$$图是$${{(}{)}}$$
A.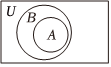
B.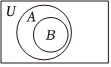
C.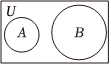
D.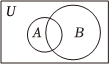
正确率60.0%“$${{x}{>}{1}}$$”是“$${{x}^{2}{>}{1}}$$”的()
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3、['分式不等式的解法', '一元二次不等式的解法', '充分、必要条件的判定']正确率60.0%$${{“}}$$不等式$$\frac{x+1} {x-1} \leqslant0$$成立$${{”}}$$是$${{“}}$$不等式$$( x-1 ) ( x+1 ) \leqslant0$$成立$${{”}}$$的$${{(}{)}}$$
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4、['一元二次不等式的解法']正确率40.0%存在$$x \in[ 0, 3 ]$$,使得不等式$$x^{2}-4 x-a \geq0$$成立,则实数$${{a}}$$的取值范围为$${{(}{)}}$$
A.$${{a}{⩽}{−}{3}}$$
B.$${{a}{⩽}{0}}$$
C.$$- 3 \leqslant a \leqslant0$$
D.$$0 \leqslant a \leqslant3$$
5、['一元二次不等式的解法', '充分、必要条件的判定', '绝对值不等式的解法']正确率60.0%$$P : | x-2 | \geqslant1, ~ ~ Q : x^{2}-3 x+2 \geqslant0$$,则$${{“}}$$非$${{P}{”}}$$是$${{“}}$$非$${{Q}{”}}$$的 ()
B
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6、['交集', '指数(型)函数的值域', '一元二次不等式的解法', '函数求定义域']正确率60.0%设集合$$M=\{x | y=\sqrt{3 x-x^{2}} \},$$$$N=\{y | y=2^{x}, x > 1 \}$$,则$${{M}{∩}{N}{=}}$$()
D
A.$$[ 0, 3 ]$$
B.$$[ 3,+\infty)$$
C.
D.$$( 2, 3 ]$$
7、['交集', '并集', '一元二次不等式的解法']正确率60.0%已知集合$$A=\{x | x < 1 \}, B=x \{x | x^{2}-x-6 < 0 \}$$,则$${{(}{)}}$$
D
A.$$A \cap B=\{x | x < 1 \}$$
B.$$A \cup B=R$$
C.$$A \cup B=\{x | x < 2 \}$$
D.$$A \cap B=\{x |-2 < x < 1 \}$$
8、['交集', '一元二次不等式的解法']正确率60.0%若集合$$A=\left\{x {\in} R \left\vert3 x {+} 2 {>} 0 \right. \right\}, B {=} \left\{x {\in} R \left\vert x^{2} {-} 2 x {-} 3 {>} 0 \right. \right\}$$,则$${{A}{∩}{B}{=}}$$
B
A.$$\{x \! \in\! R \, | x \! < \!-1 ~ \}$$
B.$$\left\{x \! \in\! R \left| x \! > \! 3 \right. \right\}$$
C.$$\left\{x \in R \left|-\frac{2} {3} < x < 3 \right. \right\}$$
D.$$\left\{x \in R \left|-1 < x <-\frac{2} {3} \right. \right\}$$
9、['交集', '一元二次不等式的解法']正确率60.0%设全集$${{U}{=}{R}}$$,集合$$A=\{y | y=\sqrt{4-x^{2}}+2 \}, \, \, \, B=\{x | x^{2}-8 x+1 5 < 0 \}$$,则$${{A}{∩}{B}}$$等于$${{(}{)}}$$
C
A.$$[ 2, 3 )$$
B.$$( 2, 4 )$$
C.$$( 3, 4 ]$$
D.$$( 2, 4 ]$$
10、['一元二次不等式的解法', '充分、必要条件的判定', '绝对值不等式的解法']正确率40.0%设$${{x}{∈}{R}}$$,则$$| x-1 | < 2^{n}$$是$$` ` x^{2}-4 x-5 < 0 "$$成立的
A
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
1. 首先解集合 $$A$$ 的不等式 $$x^2 - 3x \leq 0$$,解得 $$0 \leq x \leq 3$$。因为 $$x \in N$$,所以 $$A = \{0, 1, 2, 3\}$$。集合 $$B = \{1, 2\}$$ 是 $$A$$ 的真子集。因此,正确的 Venn 图是选项 A。
3. 解不等式 $$\frac{x+1}{x-1} \leq 0$$ 得 $$-1 \leq x < 1$$;解不等式 $$(x-1)(x+1) \leq 0$$ 得 $$-1 \leq x \leq 1$$。前者是后者的真子集,因此前者是后者的充分不必要条件,选 A。
5. 解非 $$P$$ 得 $$|x-2| < 1$$,即 $$1 < x < 3$$;解非 $$Q$$ 得 $$x^2 - 3x + 2 < 0$$,即 $$1 < x < 2$$。非 $$P$$ 包含非 $$Q$$,因此非 $$P$$ 是非 $$Q$$ 的必要不充分条件,选 B。
7. 解集合 $$B$$ 的不等式 $$x^2 - x - 6 < 0$$ 得 $$-2 < x < 3$$。集合 $$A = \{x | x < 1\}$$,因此 $$A \cap B = \{x | -2 < x < 1\}$$,选 D。
9. 集合 $$A$$ 中 $$y = \sqrt{4 - x^2} + 2$$ 的定义域为 $$-2 \leq x \leq 2$$,且 $$y \in [2, 4]$$。集合 $$B$$ 的不等式 $$x^2 - 8x + 15 < 0$$ 解得 $$3 < x < 5$$。因此 $$A \cap B = (3, 4]$$,选 C。
.jpg)