.jpg)
正确率40.0%“对任意的$$x \in( 1， ~ 4 ]，$$不等式$$x^{2}-m x+m > 0$$恒成立”的充分不必要条件是（）
D
A.$${{m}{>}{4}}$$
B.$$m < \frac{1 6} {3}$$
C.$${{m}{<}{4}}$$
D.$${{m}{<}{2}}$$
2、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '给定参数范围的恒成立问题']正确率40.0%已知函数$$f ( x )=a \operatorname{s i n} x-\operatorname{c o s} x \ ( a \in R )$$在$$x \!=\! \frac{\pi} {4}$$处取得最值，若存在$$x_{1}， x_{2}， \dots， x_{n}$$满足$$- \frac{\pi} {4} \leq x_{1} < x_{2} < \ldots< x_{n} \leq\frac{1 5 \pi} {4}$$，且$$| f ( x_{1} )-f ( x_{2} ) |+| f ( x_{2} )-f ( x_{3} ) |+\ldots+| f ( x_{n-1} )-f ( x_{n} ) |=8 \sqrt{2} \; \; ( n \geqslant2， n \in N^{*} )$$，则$${{n}}$$的最小值为$${{(}{)}}$$
B
A.$${{3}}$$
B.$${{6}}$$
C.$${{5}}$$
D.$${{4}}$$
3、['平面向量加法、减法的坐标运算'， '给定参数范围的恒成立问题']正确率40.0%已知$$A (-2， 0 )， \， \， \， B ( 2， 0 )$$，若$${{x}}$$轴上方的点$${{P}}$$满足对任意$${{λ}{∈}{R}{，}}$$恒有$$| \overrightarrow{A P}-\lambda\overrightarrow{A B} | \geq2$$成立，则$${{P}}$$点纵坐标的最小值为$${{(}{)}}$$
D
A.$$\frac{1} {4}$$
B.$$\frac{1} {2}$$
C.$${{1}}$$
D.$${{2}}$$
4、['在给定区间上恒成立问题'， '简单复合函数的导数'， '导数与单调性'， '给定参数范围的恒成立问题']正确率40.0%已知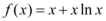
，若$${{k}{∈}{Z}}$$
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
5、['利用导数求参数的取值范围'， '给定参数范围的恒成立问题']正确率19.999999999999996%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=a l n ~ ( \begin{matrix} {x+1} \\ \end{matrix} ) ~-x^{2}$$，若对$$\forall p， ~ ~ q \in~ ( ~ 0， ~ 1 ) ~ ~，$$且$${{p}{≠}{q}}$$，有$$\frac{f ( p+1 )-f ( q+1 )} {p-q} > 2$$恒成立，则实数$${{a}}$$的取值范围为（）
C
A.$$( \ -\infty， \ 1 8 )$$
B.$$( \ -\infty， \ 1 8 ]$$
C.$$[ 1 8， ~+\infty)$$
D.$$( 1 8， ~+\infty)$$
6、['给定参数范围的恒成立问题']正确率40.0%当$$\left| m \right| \leqslant1$$时，不等式$$1-2 x < m ~ ( x^{2}-1 )$$恒成立，则$${{x}}$$的取值范围是（）
B
A.$$( \mathbf{\alpha}-\mathbf{1}， \mathbf{\alpha} 3 )$$
B.$$(-1+\sqrt{3}， \ 2 )$$
C.$$( \ -3， \ 1 )$$
D.$$( 0， ~-1+\sqrt{3} )$$
7、['函数奇、偶性的证明'， '利用导数讨论函数单调性'， '函数单调性与奇偶性综合应用'， '给定参数范围的恒成立问题']正确率60.0%已知函数$$f ( x )=2 \operatorname{s i n} x-3 x$$，若对任意的$$m \in[-2， 2 ]， \， \， \， f ( m a-3 )+f ( a^{2} ) > 0$$恒成立，则$${{a}}$$的取值范围是（）
A
A.$$(-1， 1 )$$
B.$$(-\infty，-1 ) \cup( 3，+\infty)$$
C.$$(-3， 3 )$$
D.$$(-\infty，-3 ) \cup( 1，+\infty)$$
8、['给定参数范围的恒成立问题'， '二次函数的图象分析与判断']正确率80.0%若函数$${{f}{(}{x}{)}}$$满足对于任意$$x \in\left[ n， m \right] ( n < m )$$有$$\frac{n} {k} \leqslant f ( x ) \leqslant k m$$恒成立，则称函数$${{f}{(}{x}{)}}$$在区间$$[ n， m ]$$上是$${{“}}$$被$${{k}}$$限制$${{”}}$$的，若函数$$f ( x )=x^{2}-a x+a^{2}$$在区间$$\left[ \frac1 a， a \right] ( a > 0 )$$上是$${{“}}$$被$${{2}}$$限制$${{”}}$$的，则$${{a}}$$的取值范围是（）
C
A.$$( 1， \sqrt{2} ]$$
B.$$( 1， \sqrt{\frac{3} {2}} \biggr]$$
C.$$( 1， 2 ]$$
D.$$[ \sqrt{\frac{2} {3}}， \sqrt{2} ]$$
9、['在给定区间上恒成立问题'， '绝对值不等式的解法'， '给定参数范围的恒成立问题']正确率40.0%若不等式$$| x+1 |-| x-1 | < a^{2}-a-4$$解集为空集，则实数$${{a}}$$的取值范围是
A
A.$$[-1， 2 ]$$
B.$$(-\infty，-1 ) \bigcup( 2，+\infty)$$
C.$$[-2， 3 ]$$
D.$$(-\infty，-2 ) \bigcup( 3，+\infty)$$
10、['函数奇偶性的应用'， '利用函数单调性解不等式'， '分段函数与方程、不等式问题'， '函数单调性与奇偶性综合应用'， '分段函数的单调性'， '给定参数范围的恒成立问题']正确率19.999999999999996%定义在$${{R}}$$上的函数$${{f}{(}{x}{)}}$$满足$$f ( x )-f (-x )=0$$，且当$${{x}{⩾}{0}}$$时，$$f ( x )=\left\{\begin{matrix} {-x^{2}+1， 0 \leqslant x < 1} \\ {2-2^{x}， x \geqslant1} \\ \end{matrix} \right.$$，若对任意的$$x \in[ m， m+1 ]$$，不等式$$f ( 1-x ) \leqslant f ( x+m )$$恒成立，则实数$${{m}}$$的最小值是（）
A
A.$${{−}{1}}$$
B.$$- \frac{1} {2}$$
C.$$- \frac{1} {3}$$
D.$$\frac{1} {3}$$
1、题目要求不等式 $$x^{2}-m x+m > 0$$ 对所有 $$x \in (1, 4]$$ 恒成立的充分不必要条件。首先求必要条件：
分情况讨论：
(1) 若 $$\frac{m}{2} \leq 1$$（即 $$m \leq 2$$），$$f(x)$$ 在 $$(1, 4]$$ 上单调递增，只需 $$f(1) \geq 0$$，即 $$1 - m + m = 1 > 0$$ 恒成立。
(2) 若 $$1 < \frac{m}{2} < 4$$（即 $$2 < m < 8$$），极小值在 $$x = \frac{m}{2}$$ 处取得，需 $$f\left(\frac{m}{2}\right) > 0$$，即 $$\frac{m^{2}}{4} - \frac{m^{2}}{2} + m > 0$$，解得 $$0 < m < 4$$。
(3) 若 $$\frac{m}{2} \geq 4$$（即 $$m \geq 8$$），$$f(x)$$ 在 $$(1, 4]$$ 上单调递减，需 $$f(4) > 0$$，即 $$16 - 4m + m > 0$$，解得 $$m < \frac{16}{3}$$，与 $$m \geq 8$$ 矛盾。
综上，必要条件为 $$m < 4$$。题目要求充分不必要条件，选项中 $$m < 2$$（D）是 $$m < 4$$ 的真子集，故选 D。
2、函数 $$f(x) = a \sin x - \cos x$$ 在 $$x = \frac{\pi}{4}$$ 处取得最值，说明 $$f'\left(\frac{\pi}{4}\right) = 0$$，即 $$a \cos \frac{\pi}{4} + \sin \frac{\pi}{4} = 0$$，解得 $$a = -1$$。
因此 $$f(x) = -\sin x - \cos x = -\sqrt{2} \sin\left(x + \frac{\pi}{4}\right)$$，其振幅为 $$\sqrt{2}$$。
题目要求在区间 $$\left[-\frac{\pi}{4}, \frac{15\pi}{4}\right]$$ 内，$$|f(x_{i}) - f(x_{i+1})|$$ 的和为 $$8\sqrt{2}$$。由于每个极值点间的变化量为 $$2\sqrt{2}$$，需要至少 $$4$$ 个极值点（即 $$n-1 = 4$$，$$n = 5$$）。
验证：区间内包含 $$x = \frac{\pi}{4}, \frac{5\pi}{4}, \frac{9\pi}{4}, \frac{13\pi}{4}$$ 四个极值点，总变化量为 $$4 \times 2\sqrt{2} = 8\sqrt{2}$$，故 $$n_{\text{min}} = 5$$，选 C。
3、设点 $$P(x, y)$$（$$y > 0$$），向量 $$\overrightarrow{AP} = (x + 2, y)$$，$$\overrightarrow{AB} = (4, 0)$$。
不等式 $$|\overrightarrow{AP} - \lambda \overrightarrow{AB}| \geq 2$$ 对所有 $$\lambda \in \mathbb{R}$$ 恒成立，即 $$(x + 2 - 4\lambda)^{2} + y^{2} \geq 4$$。
对 $$\lambda$$ 求最小值，当 $$\lambda = \frac{x + 2}{4}$$ 时取到最小 $$y^{2} \geq 4$$，即 $$y \geq 2$$。故 $$P$$ 点纵坐标的最小值为 $$2$$，选 D。
4、题目不完整，无法解析。
5、函数 $$f(x) = a \ln(x + 1) - x^{2}$$，不等式 $$\frac{f(p + 1) - f(q + 1)}{p - q} > 2$$ 可转化为导数不等式 $$f'(x) > 2$$ 在 $$(1, 2)$$ 上恒成立。
求导得 $$f'(x) = \frac{a}{x + 1} - 2x$$，需 $$\frac{a}{x + 1} - 2x > 2$$ 对所有 $$x \in (1, 2)$$ 成立，即 $$a > (2x + 2)(x + 1)$$。
右边函数在 $$x \in (1, 2)$$ 的最大值为 $$x = 2$$ 时 $$(6)(3) = 18$$，故 $$a \geq 18$$，选 C。
6、不等式 $$1 - 2x < m(x^{2} - 1)$$ 对所有 $$|m| \leq 1$$ 恒成立，转化为 $$1 - 2x < - (x^{2} - 1)$$ 和 $$1 - 2x < x^{2} - 1$$ 同时成立。
解得：
(1) $$x^{2} + 2x - 2 < 0$$，即 $$-1 - \sqrt{3} < x < -1 + \sqrt{3}$$；
(2) $$x^{2} + 2x - 2 > 0$$，即 $$x < -1 - \sqrt{3}$$ 或 $$x > -1 + \sqrt{3}$$。
综合得 $$-1 + \sqrt{3} < x < 2$$（注意 $$x = 1$$ 时不等式不成立），选 B。
7、函数 $$f(x) = 2 \sin x - 3x$$ 是奇函数且单调递减（因 $$f'(x) = 2 \cos x - 3 \leq -1 < 0$$）。
不等式 $$f(m a - 3) + f(a^{2}) > 0$$ 可化为 $$f(m a - 3) > -f(a^{2}) = f(-a^{2})$$，由单调性得 $$m a - 3 < -a^{2}$$。
对所有 $$m \in [-2, 2]$$ 成立，需 $$2a - 3 < -a^{2}$$ 且 $$-2a - 3 < -a^{2}$$，解得 $$a^{2} + 2a - 3 < 0$$ 和 $$a^{2} - 2a - 3 < 0$$，即 $$a \in (-3, 1) \cap (-1, 3) = (-1, 1)$$，选 A。
8、函数 $$f(x) = x^{2} - a x + a^{2}$$ 在区间 $$\left[\frac{1}{a}, a\right]$$ 上被 $$2$$ 限制，即 $$\frac{1}{2a} \leq f(x) \leq 2a$$ 对所有 $$x \in \left[\frac{1}{a}, a\right]$$ 成立。
求 $$f(x)$$ 的极值：$$f'(x) = 2x - a$$，极值点为 $$x = \frac{a}{2}$$。
分情况讨论：
(1) 若 $$\frac{a}{2} \in \left[\frac{1}{a}, a\right]$$，即 $$a \geq \sqrt{2}$$，需 $$f\left(\frac{a}{2}\right) \leq 2a$$ 且 $$f\left(\frac{1}{a}\right) \geq \frac{1}{2a}$$，解得 $$a \in \left(1, \sqrt{2}\right]$$。
(2) 若 $$\frac{a}{2} < \frac{1}{a}$$（即 $$a < \sqrt{2}$$），需 $$f\left(\frac{1}{a}\right) \leq 2a$$ 且 $$f(a) \geq \frac{1}{2a}$$，解得 $$a \in \left(1, \sqrt{\frac{3}{2}}\right]$$。
综合得 $$a \in \left(1, \sqrt{2}\right]$$，选 A。
9、不等式 $$|x + 1| - |x - 1| < a^{2} - a - 4$$ 解集为空集，意味着 $$a^{2} - a - 4 \leq \max (|x + 1| - |x - 1|)$$。
函数 $$g(x) = |x + 1| - |x - 1|$$ 的最大值为 $$2$$（当 $$x \geq 1$$ 时），故 $$a^{2} - a - 4 \leq 2$$，即 $$a^{2} - a - 6 \leq 0$$，解得 $$a \in [-2, 3]$$，选 C。
10、函数 $$f(x)$$ 为偶函数，且在 $$x \geq 0$$ 时分为两段：
(1) $$0 \leq x < 1$$ 时，$$f(x) = -x^{2} + 1$$ 单调递减；
(2) $$x \geq 1$$ 时，$$f(x) = 2 - 2^{x}$$ 单调递减。
不等式 $$f(1 - x) \leq f(x + m)$$ 需对所有 $$x \in [m, m + 1]$$ 成立。分情况讨论：
(1) 若 $$m \geq -\frac{1}{2}$$，取 $$x = m$$，得 $$f(1 - m) \leq f(2m)$$，由单调性需 $$1 - m \geq 2m$$，即 $$m \leq \frac{1}{3}$$。
(2) 若 $$m < -\frac{1}{2}$$，取 $$x = m + 1$$，得 $$f(-m) \leq f(2m + 1)$$，由偶函数和单调性需 $$-m \geq 2m + 1$$，即 $$m \leq -\frac{1}{3}$$。
综上，$$m \leq \frac{1}{3}$$，最小值为 $$-\frac{1}{2}$$（验证 $$m = -\frac{1}{2}$$ 时不等式成立），选 B。