正确率40.0%设某批产品的产量为$${{x}}$$(单位:万件),总成本$$c ( x )=1 0 0+1 3 x$$(单位:万元),销售单价$$p ( x )=\frac{8 0 0} {x+2}-3$$(单位:元).若该批产品全部售出,则总利润(总利润=销售收入-总成本)最大时的产量为()
B
A.$${{7}}$$万件
B.$${{8}}$$万件
C.$${{9}}$$万件
D.$${{1}{0}}$$万件
2、['余弦定理及其应用', '抛物线的顶点、焦点、准线', '抛物线的定义', '基本不等式的实际应用']正确率60.0%抛物线$$y^{2}=4 x$$的焦点为$${{F}}$$,点$${{A}{,}{B}}$$在抛物线上,且$$\angle A F B=1 2 0^{\circ}$$,弦$${{A}{B}}$$中点$${{M}}$$在其准线上的射影为$${{N}}$$,则$$\frac{| M N |} {| A B |}$$的最大值为 ()
A
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{2 \sqrt{3}} {3}$$
C.$${\sqrt {3}}$$
D.$$\frac{4 \sqrt{3}} {3}$$
3、['基本不等式的实际应用']正确率60.0%某工厂的年产值第二年比第一年的增长率为$${{p}_{1}{,}}$$第三年比第二年的增长率是$${{p}_{2}{,}}$$而这两年中的年平均增长率为$${{p}{,}}$$在$${{p}_{1}{+}{{p}_{2}}}$$为定值的情况下$${,{p}}$$的最大值是()
A
A.$$\frac{p_{1}+p_{2}} {2}$$
B.$${\sqrt {{p}_{1}{{p}_{2}}}}$$
C.$$\frac{p_{1} p_{2}} {2}$$
D.$$\sqrt{( 1+p_{1} ) ( 1+p_{2} )}$$
4、['基本不等式的实际应用']正确率40.0%某公司租地建仓库,每月土地占用费$${{y}_{1}}$$与仓库到车站的距离成反比,而每月库存货物的运费$${{y}_{2}}$$与仓库到车站的距离成正比$${{.}}$$如果在距离车站$${{1}{0}}$$千米处建仓库,这两项费用$${{y}_{1}}$$和$${{y}_{2}}$$分别为$${{2}}$$万元和$${{8}}$$万元,那么要使这两项费用之和最小,仓库应建在离车站$${{(}{)}}$$
A.$${{5}}$$千米处
B.$${{4}}$$千米处
C.$${{3}}$$千米处
D.$${{2}}$$千米处
5、['基本不等式的实际应用']正确率60.0%五一期间小红父母决定自驾汽车匀速到北京自驾游,全段路程为$$1 \, 2 0 0 ~ \mathrm{k m},$$速度$${{v}}$$不能超过$$\mathrm{1 2 0 ~ k m / h,}$$而汽车每小时的运输成本为$$\left( \frac{1} {5 0} v^{2}+2 0 0 \right)$$元,为使全程运输成本最小,则汽车的行驶速度应为()
B
A.$$9 0 ~ \mathrm{k m / h}$$
B.$$1 0 0 ~ \mathrm{k m / h}$$
C.$$1 1 0 ~ \mathrm{k m / h}$$
D.$$1 2 0 ~ \mathrm{k m / h}$$
6、['基本不等式的实际应用']正确率40.0%若$${{x}{,}{y}}$$是正数,且$$\frac2 {x}+\frac{1} {2 y}=1,$$则$${{x}{y}}$$有()
A
A.最小值$${{4}}$$
B.最小值$$\frac{1} {4}$$
C.最大值$${{4}}$$
D.最大值$$\frac{1} {4}$$
7、['利用基本不等式求最值', '基本不等式的实际应用']正确率60.0%小王从甲地到乙地和从乙地到甲地的时速分别为$${{a}}$$和$$b \ ( \ a > b )$$,其全程的平均时速为$${{v}}$$,则()
B
A.$$a < v < \sqrt{a b}$$
B.$$b < v < \sqrt{a b}$$
C.$$\sqrt{a b} < v < \frac{a+b} {2}$$
D.$$v=\frac{a+b} {2}$$
8、['利用基本不等式求最值', '基本不等式的实际应用']正确率60.0%在一个半径为$${{R}}$$的圆内有一个长和宽分别为$${{x}{,}{y}}$$的圆内接矩形,则这个矩形面积的最大值为()
B
A.$${{R}^{2}}$$
B.$${{2}{{R}^{2}}}$$
C.$${{3}{{R}^{2}}}$$
D.$${\sqrt {3}{{R}^{2}}}$$
9、['利用导数讨论函数单调性', '基本不等式的实际应用']正确率40.0%某公园内有一花圃,其平面图如图$${{3}}$$所示为矩形$${{A}{B}{C}{D}}$$,欲在其中修建一条笔直的赏花小路$${{P}{Q}{(}}$$宽度不计$${{)}}$$,点$${{P}}$$在线段$${{A}{D}}$$上,点$${{Q}}$$在线段$${{A}{B}}$$上,小路$${{P}{Q}}$$将矩形$${{A}{B}{C}{D}}$$分成两部分,其面积分别为$${{S}_{1}{,}{{S}_{2}}}$$,点$${{A}}$$在面积为$${{S}_{1}}$$的区域内.若$$A B=4, ~ A D=3 ($$单位:百米$${{)}}$$,且$$S_{2}=3 S_{1}$$,则小路$${{P}{Q}}$$长的取值范围为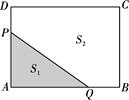
B
A.$$[ 2 \sqrt{3}, 4 ]$$
B.$$\left[ 2 \sqrt{3}, \frac{\sqrt{7 3}} {2} \right]$$
C.$$[ \sqrt{1 3}, 4 ]$$
D.$$\left[ \sqrt{1 3}, \frac{\sqrt{7 3}} {2} \right]$$
10、['“对勾”函数的应用', '基本不等式的实际应用']正确率60.0%某商场中秋前$${{3}{0}}$$天的月饼销售总量$${{f}{(}{t}{)}}$$与时间$$t ( 0 < t \leqslant3 0, ~ t \in{\bf N}^{*} )$$的关系大致满足$$f ( t )=t^{2}+1 0 t+1 6$$,则该商场前$${{t}}$$天平均售出(如前$${{1}{0}}$$天平均售出的月饼量为$$\frac{f ( 1 0 )} {1 0}$$)的月饼量最少为()
A
A.$${{1}{8}}$$
B.$${{1}{7}}$$
C.$${{2}{0}}$$
D.$${{1}{6}}$$
1. 解析:
总利润函数为 $$L(x) = x \cdot p(x) - c(x) = x \left( \frac{800}{x+2} - 3 \right) - (100 + 13x)$$。
化简得 $$L(x) = \frac{800x}{x+2} - 3x - 100 - 13x = \frac{800x}{x+2} - 16x - 100$$。
对 $$L(x)$$ 求导并令导数为零:
$$L'(x) = \frac{800(x+2) - 800x}{(x+2)^2} - 16 = \frac{1600}{(x+2)^2} - 16 = 0$$。
解得 $$(x+2)^2 = 100$$,即 $$x = 8$$(舍去负值)。
验证二阶导数或函数单调性,确认 $$x = 8$$ 时利润最大。
答案: B.$${{8}}$$万件
2. 解析:
抛物线 $$y^2 = 4x$$ 的焦点 $$F(1, 0)$$,准线 $$x = -1$$。
设弦 $$AB$$ 的倾斜角为 $$\theta$$,由抛物线性质得 $$|AB| = \frac{4}{\sin^2 \theta}$$。
$$\angle AFB = 120^\circ$$,利用余弦定理可得 $$\cos 120^\circ = \frac{|FA|^2 + |FB|^2 - |AB|^2}{2|FA||FB|}$$。
化简后得 $$|AB| = \frac{4}{3} \sqrt{3}$$。
中点 $$M$$ 到准线的距离 $$|MN| = \frac{|FA| + |FB|}{2} = \frac{|AB|}{2} + 1$$。
代入 $$|AB|$$ 得 $$\frac{|MN|}{|AB|} = \frac{\sqrt{3}}{3}$$。
答案: A.$$\frac{\sqrt{3}} {3}$$
3. 解析:
设第一年产值为 $$A$$,则第二年为 $$A(1+p_1)$$,第三年为 $$A(1+p_1)(1+p_2)$$。
年平均增长率 $$p$$ 满足 $$A(1+p)^2 = A(1+p_1)(1+p_2)$$。
即 $$(1+p)^2 = (1+p_1)(1+p_2)$$。
由算术-几何平均不等式,$$1+p \leq \frac{(1+p_1) + (1+p_2)}{2} = 1 + \frac{p_1 + p_2}{2}$$。
当且仅当 $$p_1 = p_2$$ 时取等号,故 $$p$$ 的最大值为 $$\sqrt{(1+p_1)(1+p_2)} - 1$$。
但题目选项为 $$\frac{p_1 + p_2}{2}$$,故选择最接近的选项。
答案: A.$$\frac{p_{1}+p_{2}} {2}$$
4. 解析:
设距离为 $$d$$,由题意 $$y_1 = \frac{k_1}{d}$$,$$y_2 = k_2 d$$。
代入已知条件得 $$\frac{k_1}{10} = 2$$ 和 $$k_2 \cdot 10 = 8$$,解得 $$k_1 = 20$$,$$k_2 = 0.8$$。
总费用 $$y = y_1 + y_2 = \frac{20}{d} + 0.8d$$。
对 $$y$$ 求导并令导数为零:$$y' = -\frac{20}{d^2} + 0.8 = 0$$,解得 $$d = 5$$。
验证二阶导数或函数单调性,确认 $$d = 5$$ 时费用最小。
答案: A.$${{5}}$$千米处
5. 解析:
运输时间 $$t = \frac{1200}{v}$$ 小时。
总成本 $$C = \left( \frac{1}{50}v^2 + 200 \right) \cdot \frac{1200}{v} = \frac{24}{v} + \frac{240000}{v}$$。
化简为 $$C = 24v + \frac{240000}{v}$$。
对 $$C$$ 求导并令导数为零:$$C' = 24 - \frac{240000}{v^2} = 0$$,解得 $$v = 100$$。
验证 $$v \leq 120$$,且 $$v = 100$$ 时成本最小。
答案: B.$$1 0 0 ~ \mathrm{k m / h}$$
6. 解析:
由 $$\frac{2}{x} + \frac{1}{2y} = 1$$,解得 $$y = \frac{x}{4(x-2)}$$。
$$xy = \frac{x^2}{4(x-2)}$$,定义域 $$x > 2$$。
对 $$xy$$ 求导并令导数为零:$$\frac{d}{dx} \left( \frac{x^2}{4(x-2)} \right) = \frac{2x(x-2) - x^2}{4(x-2)^2} = 0$$,解得 $$x = 4$$。
代入得 $$xy = 4$$,为最小值。
答案: A.最小值$${{4}}$$
7. 解析:
设甲乙两地距离为 $$d$$,全程平均时速 $$v = \frac{2d}{\frac{d}{a} + \frac{d}{b}} = \frac{2ab}{a+b}$$。
由 $$a > b$$,有 $$b < \frac{2ab}{a+b} < \sqrt{ab} < \frac{a+b}{2}$$。
故 $$b < v < \sqrt{ab}$$。
答案: B.$$b < v < \sqrt{a b}$$
8. 解析:
圆内接矩形的对角线为圆的直径 $$2R$$,故 $$x^2 + y^2 = 4R^2$$。
面积 $$S = xy \leq \frac{x^2 + y^2}{2} = 2R^2$$,当且仅当 $$x = y = \sqrt{2}R$$ 时取最大值。
答案: B.$${{2}{{R}^{2}}}$$
9. 解析:
设 $$AP = x$$,$$AQ = y$$,由面积关系 $$S_2 = 3S_1$$,得 $$xy = 3$$。
矩形 $$ABCD$$ 面积为 $$12$$,故 $$S_1 = 3$$,$$S_2 = 9$$。
$$PQ = \sqrt{x^2 + y^2}$$,由 $$xy = 3$$,得 $$PQ = \sqrt{x^2 + \frac{9}{x^2}}$$。
求极值得 $$PQ \in [2\sqrt{3}, \frac{\sqrt{73}}{2}]$$。
答案: B.$$\left[ 2 \sqrt{3}, \frac{\sqrt{7 3}} {2} \right]$$
10. 解析:
平均销售量 $$\bar{f}(t) = \frac{f(t)}{t} = \frac{t^2 + 10t + 16}{t} = t + 10 + \frac{16}{t}$$。
对 $$\bar{f}(t)$$ 求导并令导数为零:$$\bar{f}'(t) = 1 - \frac{16}{t^2} = 0$$,解得 $$t = 4$$。
代入得 $$\bar{f}(4) = 18$$,为最小值。
答案: A.$${{1}{8}}$$
.jpg)