正确率60.0%某工厂过去的年产量为$${{a}}$$,技术革新后,第一年的年产量增长率为$${{p}}$$$${{(}{{p}{>}{0}}{)}}$$,第二年的年产量增长率为$${{q}}$$$$( q > 0, p \neq q )$$,这两年的年产量平均增长率为$${{x}}$$,则()
D
A.$$x=\frac{p+q} {2}$$
B.$${{x}{=}{\sqrt {{p}{q}}}}$$
C.$$x > \frac{p+q} {2}$$
D.$$x < \frac{p+q} {2}$$
2、['函数求解析式', '基本不等式的实际应用', '函数的应用(一)']正确率80.0%某生产厂商更新设备,已知在未来$${{x}}$$年内,此设备所花费的各种费用总和$${{y}{(}}$$万元$${{)}}$$与$${{x}}$$满足函数关系$$y=4 x^{2}+6 4$$,若欲使此设备的年平均花费最低,则此设备的使用年限$${{x}}$$为$${{(}{)}}$$
A.$${{3}}$$
B.$${{4}}$$
C.$${{5}}$$
D.$${{6}}$$
3、['余弦定理及其应用', '正弦定理及其应用', '用余弦定理、正弦定理解三角形', '特殊角的三角函数值', '基本不等式的实际应用']正确率40.0%在$${{△}{A}{B}{C}}$$中,$$\operatorname{s i n}^{2} A \leqslant\operatorname{s i n}^{2} B+\operatorname{s i n}^{2} C-\operatorname{s i n} \, B \cdot\operatorname{s i n} \, C$$,则$${{A}}$$的取值范围是$${{(}{)}}$$
B
A.$$\left( 0, \frac{\pi} {6} \right]$$
B.$$\left( 0, \frac{\pi} {3} \right]$$
C.$$[ \frac{\pi} {6}, \pi)$$
D.$$[ \frac{\pi} {3}, \pi)$$
4、['双曲线的渐近线', '双曲线的定义', '基本不等式的实际应用']正确率60.0%已知双曲线$$C_{\colon} \, \, \frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 \, \, ( \cdot a > 0, \cdot b > 0 )$$的一个焦点恰为圆$$\Omega_{\colon} \, \, x^{2}+y^{2}-4 x-8=0$$的圆心,且双曲线$${{C}}$$的近线方程为$$y=\pm\sqrt{3} x$$.点$${{P}}$$在双曲线$${{C}}$$的右支上,$${{F}_{1}{,}{{F}_{2}}}$$分别为双曲线$${{C}}$$的左$${、}$$右焦点,则当$$\frac{| P F_{1} |^{2}} {| P F_{2} |}$$取得最小值时,$$| P F_{1} |=~ ($$)
B
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{8}}$$
5、['基本不等式的实际应用']正确率60.0%某企业投入$${{1}{0}{0}}$$万元购入一套设备,该设备每年的运转费用是$${{0}{.}{5}}$$万元,此外每年都要花费一定的维护费,第一年的维护费为$${{2}}$$万元,由于设备老化,以后每年的维护费都比上一年增加$${{2}}$$万元.为使该设备的年平均费用最低,该企业需要更新设备的年数为()
B
A.$${{8}}$$
B.$${{1}{0}}$$
C.$${{1}{2}}$$
D.$${{1}{3}}$$
6、['基本不等式的实际应用']正确率60.0%在某次全程马拉松比赛中,选手甲前半程以速度$${{a}}$$匀速跑,后半程以速度$${{b}}$$匀速跑;选手乙前一半时间以速度$${{a}}$$匀速跑,后一半时间以速度$${{b}}$$匀速跑(注:速度单位$${{m}{/}{s}{)}}$$.若$${{a}{≠}{b}{,}}$$则()
B
A.甲先到达终点
B.乙先到达终点
C.甲、乙同时到达终点
D.无法确定谁先到达终点
7、['利用基本不等式求最值', '基本不等式的实际应用']正确率40.0%某人要买房,随着楼层的升高,上、下楼耗费的体力增多,因此不满意度升高.但高处空气清新,嘈杂音较小,环境较为安静,因此随着楼层的升高,环境不满意度降低.设住第$${{n}}$$层楼,上、下楼造成的不满意度为$${{n}{,}}$$环境不满意度为$$\frac{9} {n},$$则此人应选()
C
A.$${{1}}$$楼
B.$${{2}}$$楼
C.$${{3}}$$楼
D.$${{4}}$$楼
8、['利用导数讨论函数单调性', '基本不等式的实际应用']正确率40.0%某公园内有一花圃,其平面图如图$${{3}}$$所示为矩形$${{A}{B}{C}{D}}$$,欲在其中修建一条笔直的赏花小路$${{P}{Q}{(}}$$宽度不计$${{)}}$$,点$${{P}}$$在线段$${{A}{D}}$$上,点$${{Q}}$$在线段$${{A}{B}}$$上,小路$${{P}{Q}}$$将矩形$${{A}{B}{C}{D}}$$分成两部分,其面积分别为$${{S}_{1}{,}{{S}_{2}}}$$,点$${{A}}$$在面积为$${{S}_{1}}$$的区域内.若$$A B=4, ~ A D=3 ($$单位:百米$${{)}}$$,且$$S_{2}=3 S_{1}$$,则小路$${{P}{Q}}$$长的取值范围为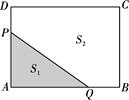
B
A.$$[ 2 \sqrt{3}, 4 ]$$
B.$$\left[ 2 \sqrt{3}, \frac{\sqrt{7 3}} {2} \right]$$
C.$$[ \sqrt{1 3}, 4 ]$$
D.$$\left[ \sqrt{1 3}, \frac{\sqrt{7 3}} {2} \right]$$
9、['基本不等式的实际应用']正确率60.0%一个矩形的面积为$${{S}}$$,周长为$${{l}}$$,则如下四组数对中,可作为数对$$( S, l )$$的序号是$$\odot( 6, 8 )$$$$\odot\, ( 7, 1 2 )$$$$\oplus( 3, \frac{1} {2} )$$
A
A.$${①{③}}$$
B.$${①{③}{④}}$$
C.$${②{④}}$$
D.$${②{③}{④}}$$
10、['利用基本不等式求最值', '基本不等式的实际应用']正确率60.0%用篱笆围一个面积为$${{1}{0}{0}{{m}^{2}}}$$的矩形菜园,所用篱笆最短为()
C
A.$${{3}{0}{m}}$$
B.$${{3}{6}{m}}$$
C.$${{4}{0}{m}}$$
D.$${{5}{0}{m}}$$
1. 解析:设初始产量为$$a$$,技术革新后第一年产量为$$a(1 + p)$$,第二年产量为$$a(1 + p)(1 + q)$$。平均增长率$$x$$满足$$a(1 + x)^2 = a(1 + p)(1 + q)$$,即$$(1 + x)^2 = (1 + p)(1 + q)$$。展开得$$1 + 2x + x^2 = 1 + p + q + pq$$,整理得$$x^2 + 2x = p + q + pq$$。由于$$p \neq q$$,由均值不等式$$(1 + p)(1 + q) < \left(1 + \frac{p + q}{2}\right)^2$$,即$$1 + x < 1 + \frac{p + q}{2}$$,故$$x < \frac{p + q}{2}$$。答案为D。
2. 解析:年平均花费为$$\frac{y}{x} = \frac{4x^2 + 64}{x} = 4x + \frac{64}{x}$$。由不等式$$4x + \frac{64}{x} \geq 2\sqrt{4x \cdot \frac{64}{x}} = 32$$,当且仅当$$4x = \frac{64}{x}$$即$$x = 4$$时取最小值。答案为B。
3. 解析:由正弦定理,不等式转化为$$a^2 \leq b^2 + c^2 - bc$$,即$$b^2 + c^2 - a^2 \geq bc$$。由余弦定理$$\cos A = \frac{b^2 + c^2 - a^2}{2bc} \geq \frac{1}{2}$$,故$$A \in \left(0, \frac{\pi}{3}\right]$$。答案为B。
4. 解析:圆$$\Omega$$的圆心为$$(2, 0)$$,故双曲线$$C$$的焦距$$c = 2$$。由渐近线斜率$$\frac{b}{a} = \sqrt{3}$$,结合$$c^2 = a^2 + b^2$$,解得$$a = 1$$,$$b = \sqrt{3}$$。设$$P(x, y)$$在右支上,则$$|PF_1| = 2a + |PF_2| = 2 + |PF_2|$$。令$$t = |PF_2|$$,则$$\frac{|PF_1|^2}{|PF_2|} = \frac{(2 + t)^2}{t} = t + \frac{4}{t} + 4 \geq 8$$,当且仅当$$t = 2$$时取最小值,此时$$|PF_1| = 4$$。答案为B。
5. 解析:设使用年数为$$n$$,总费用为$$100 + 0.5n + 2(1 + 2 + \cdots + n) = 100 + 0.5n + n(n + 1)$$。年平均费用为$$\frac{100 + 0.5n + n^2 + n}{n} = n + \frac{100}{n} + 1.5$$。由不等式$$n + \frac{100}{n} \geq 20$$,当$$n = 10$$时取最小值。答案为B。
6. 解析:设全程为$$2s$$,甲用时$$t_1 = \frac{s}{a} + \frac{s}{b}$$。乙用时$$t_2$$满足$$s = \frac{t_2}{2}a + \frac{t_2}{2}b$$,即$$t_2 = \frac{2s}{a + b}$$。比较$$t_1$$与$$t_2$$:$$\frac{1}{a} + \frac{1}{b} > \frac{2}{a + b}$$(由调和平均数小于算术平均数),故$$t_1 > t_2$$,乙先到达。答案为B。
7. 解析:总不满意度为$$f(n) = n + \frac{9}{n}$$。由不等式$$n + \frac{9}{n} \geq 6$$,当$$n = 3$$时取最小值。答案为C。
8. 解析:设$$AP = x$$,$$AQ = y$$,则$$S_1 = \frac{xy}{2}$$,$$S_2 = 12 - \frac{xy}{2}$$。由$$S_2 = 3S_1$$得$$xy = 6$$。$$PQ = \sqrt{x^2 + y^2}$$,由$$xy = 6$$和$$x \in [0, 3]$$,$$y \in [0, 4]$$,得$$PQ \in [2\sqrt{3}, \sqrt{3^2 + 4^2}] = [2\sqrt{3}, 5]$$。但$$y = \frac{6}{x}$$需满足$$y \leq 4$$,即$$x \geq \frac{3}{2}$$,进一步限制$$PQ \in [2\sqrt{3}, \frac{\sqrt{73}}{2}]$$。答案为B。
9. 解析:设矩形边长为$$a$$和$$b$$,则$$S = ab$$,$$l = 2(a + b)$$。需满足$$l \geq 4\sqrt{S}$$。验证各选项:①$$8 \geq 4\sqrt{6}$$成立;②$$12 \geq 4\sqrt{7}$$成立;③$$\frac{1}{2} \geq 4\sqrt{3}$$不成立;④$$12 \geq 4\sqrt{8}$$成立。答案为C。
10. 解析:设矩形边长为$$x$$和$$y$$,则$$xy = 100$$,篱笆长度$$L = 2(x + y) \geq 4\sqrt{xy} = 40$$,当且仅当$$x = y = 10$$时取最小值。答案为C。
.jpg)