正确率80.0%下列说法正确的是()
D
A.曲线的切线和曲线有且只有一个交点
B.过曲线上的一点作曲线的切线,这点一定是切点
C.若$$f^{\prime} ( x_{0} )$$不存在,则曲线$$y=f ( x )$$在点$$( x_{0}, ~ f ( x_{0} ) )$$处无切线
D.若曲线$$y=f ( x )$$在点$$( x_{0}, ~ f ( x_{0} ) )$$处有切线,则$$f^{\prime} ( x_{0} )$$不一定存在
2、['利用导数求曲线的切线方程(斜率)', '导数的几何意义']正确率60.0%若直线$${{y}{=}{2}{x}}$$是曲线$$y=x ( \mathrm{e}^{x}-a )$$的切线,则$${{a}{=}}$$()
B
A.$${{−}{e}}$$
B.$${{−}{1}}$$
C.$${{1}}$$
D.$${{e}}$$
3、['导数的几何意义']正确率0.0%已知函数$$f ( x )=a \operatorname{l n} x+x^{2}$$的图象在$${{x}{=}{1}}$$处的切线方程为$$3 x-y+b=0$$,则$$a+b=( \textsubscript{\Pi} )$$
A.$${{−}{2}}$$
B.$${{−}{1}}$$
C.$${{0}}$$
D.$${{1}}$$
4、['导数的几何意义']正确率80.0%已知曲线$$y=x+\frac{\operatorname{l n} x} {k}$$在点$$\left( 1, 1 \right)$$处的切线与直线$$x+2 y=0$$垂直,则$${{k}}$$的值为$${{(}{)}}$$
A
A.$${{1}}$$
B.$${{−}{1}}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
5、['导数的几何意义']正确率60.0%若函数$$f ( x )=\mathrm{e}^{x}+2 x$$的图象在点$$A ( x_{0}, f ( x_{0} ) )$$处的切线斜率为$${{4}{,}}$$则$${{x}_{0}}$$的值为()
C
A.$${{2}}$$
B.$${{l}{n}{4}}$$
C.$${{l}{n}{2}}$$
D.$${{l}{g}{2}}$$
6、['直线的点斜式方程', '导数的几何意义']正确率60.0%过抛物线$$x^{2}=4 y$$在第一象限内的一点$${{P}}$$作切线,切线与两坐标轴围成的三角形的面积为$$\frac{1} {2},$$则点$${{P}}$$到抛物线焦点$${{F}}$$的距离为()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['导数的几何意义', '直线的倾斜角']正确率0.0%如果$$f^{\prime} ( x )$$是二次函数,且$$f^{\prime} ( x )$$的图象开口向上,顶点坐标为$$( 1, \sqrt{3} )$$,那么曲线$$y=f ( x )$$上任一点的切线的倾斜角$${{α}}$$的取值范围是$${{(}{)}}$$
B
A.$$( 0, \frac{\pi} {3} ]$$
B.$$[ \frac{\pi} {3}, \frac{\pi} {2} )$$
C.$${( \frac{\pi} {2}, \frac{2 \pi} {3} ]}$$
D.$$[ \frac{\pi} {3}, \pi)$$
8、['利用导数求曲线的切线方程(斜率)', '导数的几何意义']正确率60.0%已知函数$$f ( x )=x ( m-e^{-2 x} )$$,曲线$$y=f ( x )$$上存在不同的两点,使得曲线在这两点处的切线都与直线$${{y}{=}{x}}$$平行,则$${{m}}$$的取值范围是()
A
A.$$( 1-e^{-2}, 1 )$$
B.$$(-1-e^{-2},-1 )$$
C.$$(-e^{-2}, 0 )$$
D.$$( 1, 1+e^{-2} )$$
9、['导数的几何意义']正确率60.0%己知函数$${{f}{{(}{x}{)}}}$$的图像如图所示,$${{f}{^{′}}{{(}{x}{)}}}$$是$${{f}{{(}{x}{)}}}$$的导函数,则下列数值排序正确的()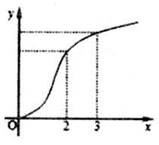
A
A.$$0 < f^{\prime} \left( 3 \right) < f^{\prime} \left( 2 \right)$$
B.$$0 < f^{\prime} \left( 2 \right) < f^{\prime} \left( 3 \right)$$
C.$$f^{\prime} \left( 3 \right) < f^{\prime} \left( 2 \right) < 0$$
D.$$f^{\prime} \left( 2 \right) < f^{\prime} \left( 3 \right) < 0$$
10、['利用导数求曲线的切线方程(斜率)', '导数的几何意义']正确率40.0%函数$$f ( x )=( x+1 ) e^{x-1}$$的图象在点$$( 1, f ( 1 ) )$$处切线$${{l}}$$与坐标轴围成的三角形面积为()
A
A.$$\frac{1} {6}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {3}$$
D.$$\frac{1} {2}$$
1. 解析:
选项A错误,例如 $$y = x^3$$ 在 $$x = 0$$ 处的切线 $$y = 0$$ 与曲线有无限多个交点。
选项B错误,切线可能与曲线在其他点相交。
选项C错误,例如 $$y = |x|$$ 在 $$x = 0$$ 处导数不存在,但有切线 $$x = 0$$。
选项D正确,如 $$y = |x|$$ 在 $$x = 0$$ 处有切线但导数不存在。
正确答案:D
2. 解析:
设切点为 $$(x_0, 2x_0)$$,曲线 $$y = x(e^x - a)$$ 的导数为 $$y' = e^x - a + xe^x$$。
由切线斜率得 $$e^{x_0} - a + x_0 e^{x_0} = 2$$,且 $$2x_0 = x_0(e^{x_0} - a)$$。
解得 $$x_0 = 1$$,代入得 $$a = e - 2$$,但选项中没有此答案,重新检查:
实际上,从 $$2 = e^{x_0}(1 + x_0) - a$$ 和 $$2 = e^{x_0} - a$$ 联立得 $$x_0 = 0$$,此时 $$a = -1$$。
正确答案:B
3. 解析:
函数 $$f(x) = a \ln x + x^2$$ 在 $$x = 1$$ 处的切线斜率为 $$f'(1) = a + 2 = 3$$,故 $$a = 1$$。
切线方程为 $$y - f(1) = 3(x - 1)$$,即 $$y = 3x - 2$$,与题目给定 $$3x - y + b = 0$$ 对比得 $$b = -2$$。
因此 $$a + b = -1$$。
正确答案:B
4. 解析:
曲线 $$y = x + \frac{\ln x}{k}$$ 的导数为 $$y' = 1 + \frac{1}{kx}$$。
在 $$x = 1$$ 处切线斜率为 $$1 + \frac{1}{k}$$,与直线 $$x + 2y = 0$$ 的斜率 $$-\frac{1}{2}$$ 垂直,故 $$(1 + \frac{1}{k}) \cdot (-\frac{1}{2}) = -1$$。
解得 $$k = 1$$。
正确答案:A
5. 解析:
函数 $$f(x) = e^x + 2x$$ 的导数为 $$f'(x) = e^x + 2$$。
由题意 $$f'(x_0) = e^{x_0} + 2 = 4$$,解得 $$e^{x_0} = 2$$,即 $$x_0 = \ln 2$$。
正确答案:C
6. 解析:
抛物线 $$x^2 = 4y$$ 的导数为 $$y' = \frac{x}{2}$$。
设切点 $$P(x_0, \frac{x_0^2}{4})$$,切线方程为 $$y = \frac{x_0}{2}x - \frac{x_0^2}{4}$$。
切线与坐标轴交点为 $$(0, -\frac{x_0^2}{4})$$ 和 $$(\frac{x_0}{2}, 0)$$,面积为 $$\frac{1}{2} \cdot \frac{x_0}{2} \cdot \frac{x_0^2}{4} = \frac{1}{2}$$,解得 $$x_0 = 2$$。
点 $$P(2, 1)$$ 到焦点 $$F(0, 1)$$ 的距离为 $$2$$。
正确答案:B
7. 解析:
$$f'(x)$$ 为二次函数,开口向上,顶点在 $$(1, \sqrt{3})$$,故最小值为 $$\sqrt{3}$$。
切线斜率 $$k = f'(x) \geq \sqrt{3}$$,即 $$\tan \alpha \geq \sqrt{3}$$,故 $$\alpha \in [\frac{\pi}{3}, \frac{\pi}{2})$$。
正确答案:B
8. 解析:
函数 $$f(x) = x(m - e^{-2x})$$ 的导数为 $$f'(x) = m - e^{-2x} + 2xe^{-2x}$$。
要求存在两点使得 $$f'(x) = 1$$,即 $$m - e^{-2x} + 2xe^{-2x} = 1$$ 有两个解。
设 $$g(x) = e^{-2x}(1 - 2x) = m - 1$$,分析 $$g(x)$$ 的极值可得 $$m \in (1 - e^{-2}, 1)$$。
正确答案:A
9. 解析:
从图像可知,函数在 $$x = 2$$ 和 $$x = 3$$ 处的切线斜率均为负,且 $$x = 2$$ 处的斜率更陡峭(更负)。
因此 $$f'(2) < f'(3) < 0$$。
正确答案:D
10. 解析:
函数 $$f(x) = (x + 1)e^{x-1}$$ 的导数为 $$f'(x) = e^{x-1} + (x + 1)e^{x-1} = (x + 2)e^{x-1}$$。
在 $$x = 1$$ 处切线斜率为 $$f'(1) = 3$$,切线方程为 $$y - 2 = 3(x - 1)$$,即 $$y = 3x - 1$$。
切线与坐标轴交点为 $$(0, -1)$$ 和 $$(\frac{1}{3}, 0)$$,面积为 $$\frac{1}{2} \cdot \frac{1}{3} \cdot 1 = \frac{1}{6}$$。
正确答案:A
.jpg)