.jpg)
正确率60.0%函数$$f ( x )=x^{2}$$在区间$$[ 0， \ 2 ]$$上的平均变化率等于该函数在$${{x}{=}{m}}$$处的瞬时变化率，则$${{m}{=}}$$（）
B
A.$$\frac{1} {2}$$
B.$${{1}}$$
C.$${{2}}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
2、['导数的四则运算法则'， '瞬时变化率']正确率80.0%空间中的某质点$${{M}}$$按规律$$s=2 t^{2}+3$$运动，则质点在$${{t}{=}{2}}$$时的瞬时速度为（）
B
A.$${{4}}$$
B.$${{8}}$$
C.$${{1}{1}}$$
D.$${{1}{6}}$$
3、['导数的几何意义'， '瞬时变化率']正确率60.0%一个质量$$m=5 ~ \mathrm{k g}$$的物体做直线运动，运动距离$${{s}}$$$${{(}}$$单位：$${{m}{)}}$$与时间$${{t}}$$(单位：$${{s}{)}}$$的关系可用函数$$s ( t )=t+\frac{1} {2} t^{2}$$表示，并且物体的动能$$E_{k}={\frac{1} {2}} m v^{2} ( m$$为物体质量$${，{v}}$$为物体运动速度$${{)}}$$，则物体开始运动后第$${{7}{s}}$$时的动能是（）
A
A.$${{1}{6}{0}{J}}$$
B.$${{1}{6}{5}{J}}$$
C.$${{1}{7}{0}{J}}$$
D.$${{1}{7}{5}{J}}$$
4、['建立函数模型解决实际问题'， '瞬时变化率'， '图象法']正确率60.0%如图所示，液体从一个圆锥形漏斗漏入一个圆柱形桶中，开始时漏斗中盛满液体，经过$${{3}}$$秒漏完，圆柱形桶中液面上升的速度是一个常量，则漏斗中液面下降的高度$${{H}}$$与下降时间$${{t}}$$之间的函数关系对应的图像只可能是（）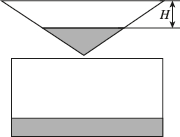
B
A.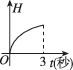
B.
C.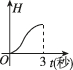
D.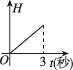
正确率60.0%一质点做直线运动，由始点经过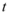
秒后的距离为
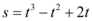，则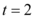
秒时的瞬时速度为（）
B
A.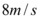
B.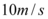
C.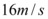
D.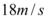
正确率60.0%已知物体的运动方程为$$s=t^{2}+\frac{3} {t}+\operatorname{l n} t-1 ( t$$是时间，$${{s}}$$是位移$${{)}}$$，则物体在时刻$${{t}{=}{3}}$$时的速度为（）
C
A.$$2 \frac{m} {s}$$
B.$$4 \frac{m} {s}$$
C.$$6 \frac{m} {s}$$
D.$$8 \frac{m} {s}$$
7、['利用导数解决实际应用问题'， '瞬时变化率']正确率60.0%一辆汽车按规律$$s=3 t^{2}+1$$做直线运动，若汽车在$${{t}{=}{2}}$$时的瞬时速度为$${{(}{)}}$$
A
A.$${{1}{2}}$$
B.$${{1}{6}}$$
C.$${{8}}$$
D.$${{4}}$$
8、['利用导数解决实际应用问题'， '瞬时变化率']正确率80.0%如果说某物体作直线运动的时间与距离满足$$s ( t )=2 ( 1-t )^{2}$$，则其在$${{t}{=}{{1}{.}{2}}}$$时的瞬时速度为（）
D
A.$${{4}}$$
B.$${{−}{4}}$$
C.$${{4}{.}{8}}$$
D.$${{0}{.}{8}}$$
9、['瞬时变化率']正确率60.0%一个物体的运动方程是$$s=1-t+t^{2}，$$其中$${{s}}$$的单位是$${{m}{，}{t}}$$的单位是$${{s}{，}}$$那么该物体在$${{t}{=}{3}{s}}$$时的瞬时速度是（）
C
A.$${{7}{m}{/}{s}}$$
B.$${{6}{m}{/}{s}}$$
C.$${{5}{m}{/}{s}}$$
D.$${{8}{m}{/}{s}}$$
10、['变化率'， '瞬时变化率']正确率60.0%甲、乙两人在一次赛跑中从同一地点出发，路程$${{S}}$$与时间$${{t}}$$的函数关系如图所示，则下列说法正确的是 （）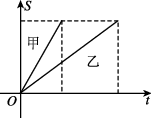
D
A.甲比乙先出发
B.乙比甲跑的路程多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
1. 解析：
函数 $$f(x) = x^2$$ 在区间 $$[0, 2]$$ 上的平均变化率为：
$$\frac{f(2) - f(0)}{2 - 0} = \frac{4 - 0}{2} = 2$$
瞬时变化率为导数 $$f'(x) = 2x$$，设在 $$x = m$$ 处瞬时变化率等于平均变化率：
$$2m = 2 \Rightarrow m = 1$$
答案为 $$\boxed{B}$$。
2. 解析：
质点运动规律 $$s = 2t^2 + 3$$，瞬时速度为导数：
$$v(t) = \frac{ds}{dt} = 4t$$
在 $$t = 2$$ 时的瞬时速度为：
$$v(2) = 4 \times 2 = 8$$
答案为 $$\boxed{B}$$。
3. 解析：
运动距离函数 $$s(t) = t + \frac{1}{2}t^2$$，速度为导数：
$$v(t) = \frac{ds}{dt} = 1 + t$$
在 $$t = 7$$ 时的速度为：
$$v(7) = 1 + 7 = 8 \, \text{m/s}$$
动能公式 $$E_k = \frac{1}{2}mv^2$$，代入数据：
$$E_k = \frac{1}{2} \times 5 \times 8^2 = 160 \, \text{J}$$
答案为 $$\boxed{A}$$。
4. 解析：
圆锥形漏斗的体积与高度关系为 $$V \propto H^3$$，液面下降速度与时间的关系为非线性，且开始时下降较快，后来变缓。图像应表现为减速下降，符合选项 $$\boxed{B}$$。
5. 解析：
题目描述不完整，无法解析。
6. 解析：
运动方程 $$s = t^2 + \frac{3}{t} + \ln t - 1$$，速度为导数：
$$v(t) = 2t - \frac{3}{t^2} + \frac{1}{t}$$
在 $$t = 3$$ 时的速度为：
$$v(3) = 6 - \frac{1}{3} + \frac{1}{3} = 6 \, \text{m/s}$$
答案为 $$\boxed{C}$$。
7. 解析：
运动规律 $$s = 3t^2 + 1$$，瞬时速度为导数：
$$v(t) = 6t$$
在 $$t = 2$$ 时的瞬时速度为：
$$v(2) = 12$$
答案为 $$\boxed{A}$$。
8. 解析：
运动方程 $$s(t) = 2(1 - t)^2$$，速度为导数：
$$v(t) = -4(1 - t)$$
在 $$t = 1.2$$ 时的瞬时速度为：
$$v(1.2) = -4(1 - 1.2) = 0.8$$
答案为 $$\boxed{D}$$。
9. 解析：
运动方程 $$s = 1 - t + t^2$$，速度为导数：
$$v(t) = -1 + 2t$$
在 $$t = 3$$ 时的瞬时速度为：
$$v(3) = -1 + 6 = 5 \, \text{m/s}$$
答案为 $$\boxed{C}$$。
10. 解析：
从图像可知，甲和乙同时出发，但甲先到达终点，且两人路程相同。因此，正确答案为 $$\boxed{D}$$。