正确率80.0%圆的面积$${{S}}$$关于半径$${{r}}$$的函数是$$S=\pi r^{2},$$那么在$${{r}{=}{3}}$$时圆面积的变化率是()
D
A.$${{6}}$$
B.$${{9}}$$
C.$${{9}{π}}$$
D.$${{6}{π}}$$
2、['平均变化率与函数的单调性', '变化率']正确率80.0%函数$$f ( x )=\sqrt{x}$$在$$[ 0, \ 2 ]$$上的平均变化率为()
A
A.$$\frac{\sqrt2} {2}$$
B.$${{1}}$$
C.$${{0}}$$
D.$${{2}}$$
3、['平均变化率与函数的单调性', '变化率']正确率80.0%函数$$f ( x )=x^{3}$$在区间$$[ 2, \ 3 ]$$上的平均变化率为()
C
A.$${{1}}$$
B.$${{9}}$$
C.$${{1}{9}}$$
D.$${{3}{6}}$$
4、['平均变化率与函数的单调性', '变化率']正确率60.0%函数$${{y}{=}{{x}^{2}}}$$在区间$$[ x_{0}, ~ x_{0}+\Delta x ]$$上的平均变化率为$${{k}_{1}{,}}$$在$$[ x_{0}-\Delta x, ~ x_{0} ]$$上的平均变化率为$${{k}_{2}{,}}$$则$${{k}_{1}}$$与$${{k}_{2}}$$的大小关系是()
A
A.$${{k}_{1}{>}{{k}_{2}}}$$
B.$${{k}_{1}{<}{{k}_{2}}}$$
C.$${{k}_{1}{=}{{k}_{2}}}$$
D.不确定
5、['平均变化率与函数的单调性', '变化率']正确率80.0%已知函数$$f ( x )=x^{2}+2 x$$,则$${{f}{(}{x}{)}}$$从$${{1}}$$到$${{1}{+}{Δ}{x}}$$的平均变化率为()
C
A.$$( \Delta x )^{2}+4 \Delta x+3$$
B.$$( \Delta x )^{2}+4 \Delta x$$
C.$${{Δ}{x}{+}{4}}$$
D.$${{4}}$$
6、['导数的概念', '变化率']正确率60.0%已知曲线$$y=\frac{1} {x^{2}}$$上两点$$P ( 1, \ 1 )$$和$$Q ( 1+\Delta x, ~ 1+\Delta y ),$$当$$\Delta x=\frac{1} {2}$$时,直线$${{P}{Q}}$$的斜率为()
B
A.$$- \frac{5} {3}$$
B.$$- \frac{1 0} {9}$$
C.$$\frac{5} {3}$$
D.$$\frac{5} {6}$$
7、['导数的概念', '变化率', '导数的几何意义']正确率60.0%已知函数$$y=f ~ ( x )$$,下列说法错误的是()
C
A.$$\triangle y=f \left( \begin{matrix} {x_{0}+\triangle x} \\ \end{matrix} \right) \ -f \left( \begin{matrix} {x_{0}} \\ \end{matrix} \right)$$叫函数增量
B.$$\frac{\triangle y} {\triangle x}=\frac{f ( x_{0}+\triangle x )-f ( x_{0} )} {\triangle x}$$叫函数在$$[ x_{0}, ~ x_{0}+\triangle x ]$$上的平均变化率
C.$${{f}{(}{x}{)}}$$在点$${{x}_{0}}$$处的导数记为$${{y}^{′}}$$
D.$${{f}{(}{x}{)}}$$在点$${{x}_{0}}$$处的导数记为$$f^{\prime} ~ ( \textbf{x}_{0} )$$
8、['变化率']正确率80.0%如图所示,函数$$y=f ( x )$$的图象过$${{A}{,}{B}}$$两点间的平均变化率等于()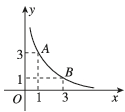
B
A.$${{1}}$$
B.$${{−}{1}}$$
C.$${{2}}$$
D.$${{−}{2}}$$
9、['导数的概念', '变化率']正确率60.0%函数$$f ~ ( \textbf{x} ) ~=x, ~ g ~ ( \textbf{x} ) ~=x^{2}$$在$$[ 0, \ 1 ]$$的平均变化率分别记为$${{m}_{1}{,}{{m}_{2}}}$$,则下面结论正确的是()
A
A.$${{m}_{1}{=}{{m}_{2}}}$$
B.$${{m}_{1}{>}{{m}_{2}}}$$
C.$${{m}_{2}{>}{{m}_{1}}}$$
D.$${{m}_{1}{,}{{m}_{2}}}$$的大小无法确定
10、['导数的概念', '变化率']正确率80.0%自变量$${{x}}$$从$${{x}_{0}}$$变到$${{x}_{1}}$$时,函数值的增量与相应自变量的增量之比是函数()
A
A.从$${{x}_{0}}$$到$${{x}_{1}}$$的平均变化率
B.在$${{x}{=}{{x}_{1}}}$$处的变化率
C.在$${{x}{=}{{x}_{1}}}$$处的变化量
D.在区间$$[ x_{0}, ~ x_{1} ]$$上的导数
1. 圆的面积函数为 $$S=\pi r^2$$,求 $$r=3$$ 时的变化率即求导数:
$$S' = \frac{dS}{dr} = 2\pi r$$
代入 $$r=3$$ 得 $$S' = 6\pi$$,故选 D。
2. 函数 $$f(x)=\sqrt{x}$$ 在 $$[0, 2]$$ 上的平均变化率为:
$$\frac{f(2)-f(0)}{2-0} = \frac{\sqrt{2}-0}{2} = \frac{\sqrt{2}}{2}$$,故选 A。
3. 函数 $$f(x)=x^3$$ 在 $$[2, 3]$$ 上的平均变化率为:
$$\frac{f(3)-f(2)}{3-2} = \frac{27-8}{1} = 19$$,故选 C。
4. 对于 $$y=x^2$$,在 $$[x_0, x_0+\Delta x]$$ 上的平均变化率 $$k_1$$ 和在 $$[x_0-\Delta x, x_0]$$ 上的平均变化率 $$k_2$$ 分别为:
$$k_1 = \frac{(x_0+\Delta x)^2 - x_0^2}{\Delta x} = 2x_0 + \Delta x$$
$$k_2 = \frac{x_0^2 - (x_0-\Delta x)^2}{\Delta x} = 2x_0 - \Delta x$$
因为 $$\Delta x > 0$$,所以 $$k_1 > k_2$$,故选 A。
5. 函数 $$f(x)=x^2+2x$$ 从 $$1$$ 到 $$1+\Delta x$$ 的平均变化率为:
$$\frac{f(1+\Delta x)-f(1)}{\Delta x} = \frac{(1+\Delta x)^2 + 2(1+\Delta x) - 3}{\Delta x}$$
化简得 $$\Delta x + 4$$,故选 C。
6. 曲线 $$y=\frac{1}{x^2}$$ 上两点 $$P(1,1)$$ 和 $$Q(1+\Delta x, 1+\Delta y)$$,当 $$\Delta x=\frac{1}{2}$$ 时:
$$Q$$ 的纵坐标为 $$y_Q = \frac{1}{(1.5)^2} = \frac{4}{9}$$
斜率 $$k = \frac{\Delta y}{\Delta x} = \frac{\frac{4}{9}-1}{\frac{1}{2}} = -\frac{10}{9}$$,故选 B。
7. 选项 C 和 D 描述导数的记号,但 D 中 $$f'(x_0)$$ 是正确的,而 C 中 $$y'$$ 是函数的导数记号,不是点 $$x_0$$ 处的导数,因此 C 错误,故选 C。
8. 图中 $$A$$ 和 $$B$$ 的坐标分别为 $$(1, 2)$$ 和 $$(3, 0)$$,平均变化率为:
$$\frac{0-2}{3-1} = -1$$,故选 B。
9. 函数 $$f(x)=x$$ 和 $$g(x)=x^2$$ 在 $$[0,1]$$ 上的平均变化率分别为:
$$m_1 = \frac{1-0}{1-0} = 1$$
$$m_2 = \frac{1-0}{1-0} = 1$$
因此 $$m_1 = m_2$$,故选 A。
10. 自变量从 $$x_0$$ 到 $$x_1$$ 时,函数增量与自变量增量之比是平均变化率的定义,故选 A。
.jpg)